本チュートリアルに関してのご質問は、SIGNATEにて開催中のコンペティションサイト( https://signate.jp/competitions/443 )のフォーラムにおきまして、新規のスレッド(ディスカッション)にてご質問していただけますと幸いです。
また、本チュートリアルに関してのご要望があれば、Githubリポジトリ( https://github.com/JapanExchangeGroup/J-Quants-Tutorial )の Issues からご意見をいただけますと幸いです。 (なお、投稿の際には、過去に同じご要望がないかご確認ください。)
-
更新履歴
2021-01-29: 初版リリース 2021-02-05: 誤字や表記の修正を中心に改良 2021-02-12: ランタイム環境のデータの扱い、GoogleColaboratoryについて追記 2021-02-19: predictor.pyの修正、stocklabelsAPIの修正 2021-02-26: 予測対象のエッジケースにおいて追記 2021-03-19: 問題2のチュートリアルを追加 2021-03-29: 問題2のチュートリアルを一部修正 2021-04-09: backtest.pyの修正(株式分割の対応) 2021-04-16: 3章の加筆
1. はじめに
証券市場では、長年、様々なデータや数学的手法を用いて市場を分析したり、金融商品の組成や投資戦略の立案が行われたりしてきました。以前はこのような分析を行うことができるのは、金融機関や機関投資家と呼ばれる大手の投資家に限られてきました。しかし近年では、個人の方にも、ITやデータを活用した金融市場の分析や取引が拡大しています。
日本取引所グループは、証券分野におけるデータ活用や人工知能の活用を発展させたいと考えています。日本においてもさまざまなデータの活用やデータサイエンティストの育成が推進されていますが、金融分野に特化したチュートリアルの作成やコンペティションはあまり行われてきていませんでした。
そこで、日本取引所グループは、投資にまつわるデータ・環境を提供し、個人投資家の皆様によるデータ利活用の可能性を検証するための実証実験プロジェクトとして、J-Quantsを立ち上げました。本プロジェクトでは、「ファンダメンタルズ分析チャレンジ」と「ニュース分析チャレンジ」の2本のコンペティションの開催を予定しています。本ページでは、これらのコンペティションに係る学習環境という位置付けで、ハンズオン形式のチュートリアルを提供します。本チュートリアルを学ぶことで、データサイエンスを活用した株価予測を行う際に、最低限必要な知識や実践方法を学ぶことができます。
本コンペティションは幅広い方にご参加いただけることを期待していますが、プログラミングの経験があり確率・統計の基礎などを勉強された学生の方や、他分野でのデータ分析経験をお持ちの社会人の方、金融分野での知見はあるがデータサイエンスについてこれから勉強をされたいと考えている社会人の方には特に楽しんでいただける内容となっています。
本チュートリアル及び本コンペティションを通じて金融データやデータ分析について理解を深めていただき、ポートフォリオ分析や資産運用に活用いただきたいと考えています。また、データサイエンスを学ぶ学生の方々にとっては、金融データを用いたデータ活用や人工知能の活用に関する研究にも興味を持っていただきたいと考えています。
| 本プロジェクトの概要やハンズオンで使うソースコード類は以下のページで公開しています。 |
プロジェクト概要 |
|
チュートリアル |
|
Jupyterノートブック |
https://github.com/JapanExchangeGroup/J-Quants-Tutorial/tree/main/handson/ |
J-QuantsAPI |
|
ファンダメンタルズ分析チャレンジ |
|
ニュース分析チャレンジ |
2. 財務諸表で株価の先行きを予測しよう
本章では、J-Quantsで開催するコンペティションのうち、「ファンダメンタルズ分析チャレンジ」(https://signate.jp/competitions/423)に係るチュートリアルを提供します。本コンペティションでは、データ分析や株式取引には興味はあるが、きっかけがないという方を主な対象として、投資にまつわるデータ・環境を提供し、株式市場におけるデータ利活用の可能性を試していただくことを期待しています。
スケジュール
| 日時 | 内容 |
|---|---|
2021年1月29日(金) |
コンペティション開始 |
2021年3月28日(日) |
モデル提出締切 |
2021年3月29日(月) 〜 6月14日(月) |
モデル評価期間 |
2021年7月頃 |
入賞者の決定 |
本コンペティションでは、東証上場企業(普通株式のみ。ETF及びREITは除きます。)が、決算短信(本資料では、四半期決算短信や訂正開示等を総称し、決算短信と表記します。)を発表した後の20営業日の間における、当該企業の株価の最高値及び最安値を、銘柄情報・株価情報・ファンダメンタル情報等を用いて予測いただきます。
コンペティションの概要
| 項目 | 内容 |
|---|---|
コンペティション名 |
ファンダメンタルズ分析チャレンジ |
主な対象者 |
株式市場を対象としたデータ分析の初学者 |
入力内容(利用データ) |
銘柄情報・株価情報・ファンダメンタル情報等 |
出力内容(予測対象) |
各東証上場企業が、決算短信を発表した後の20営業日の間における、当該企業の株価の最高値及び最安値 |
参加を通じて得られる知見 |
- 株価や企業業績の推移などの時系列データの解析手法 |
本章の構成は、まず、2.1節にて、本コンペティションにおける予測対象等の詳細について説明し、2.2節にて、本コンペティションで提供するデータセットの仕様について説明します。そして、2.3節以降で、本コンペティションのベースラインモデルの開発からモデル提出までの一連のフローを説明します。
2.1. 予測対象
本コンペティションの予測対象は、東証上場企業が、決算短信を発表した後の20営業日の期間における、当該企業の株価の最高値及び最安値です。 上場企業は決算期末を含め四半期毎に決算内容が定まった際、決算内容の開示が義務付けられています。決算の内容として開示される決算短信には財務諸表が添付されており、財務諸表は企業のファンダメンタル情報を含む複数の表で構成されています。
2.1.1項では予測対象の銘柄について、2.1.2項では予測対象の決算短信について、2.1.3項では本コンペティションの評価方法について、2.1.4項では本コンペティションのリーダーボードの仕様について、2.1.5項では決算短信と財務諸表の概要について、それぞれ説明します。
2.1.1. 予測対象の銘柄
本コンペティションの予測対象となる銘柄は、次に挙げる条件を全て満たします。
A) 2020年12月末日時点で、東京証券取引所に上場していること
B) 普通株式であること(種類株ではないこと)
C) ETF、ETN、REIT、優先出資証券、インフラファンド、外国株のいずれにも該当しないこと
D) 2020年12月末日時点で、上場後2年を経過していること
2.1.2. 予測対象の決算短信
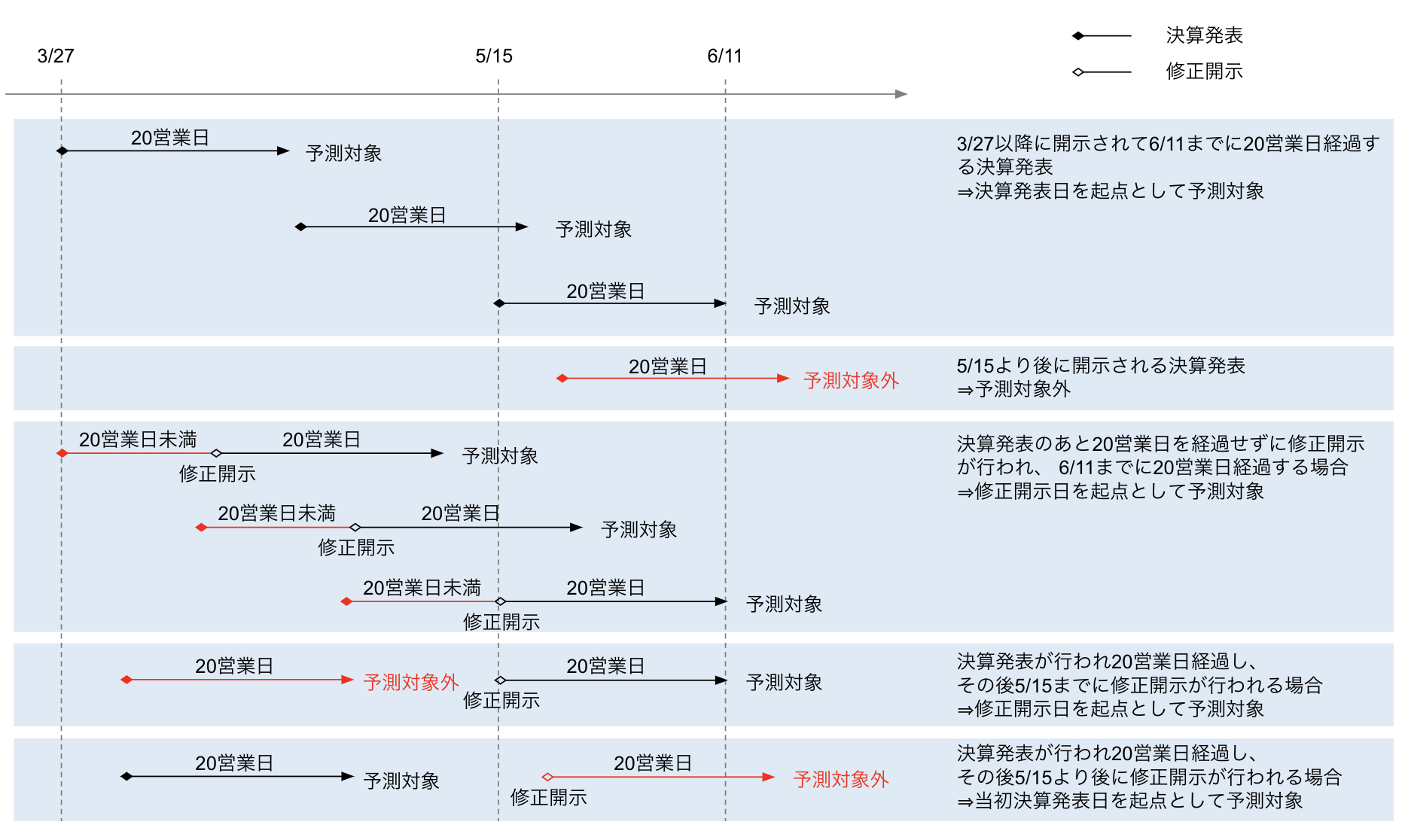
本コンペティションでは、2021年3月27日から同年5月15日の期間中に開示された決算短信を対象に、その開示日から起算して20営業日を経過した期間における、各銘柄の最高値及び最安値を予測します。厳密には、本コンペティションで予測対象となる決算短信は、次に挙げる条件を全て満たします。
A) 直近の決算期末または四半期期末に係る決算短信であること
B) 2021年3月27日から同年5月15日までの期間に開示されていること
C) 開示日及び同日から起算して20営業日を経過した日までの期間、訂正開示等が行われていないこと
D) 開示日及び同日から起算して20営業日を経過した日までの期間、上場廃止になっていないこと
条件Cに示す「訂正開示等」とは、決算発表資料の訂正、業績予想の修正・予想値と決算値との差異等、配当予想・配当予想の修正にかかる開示を指します。これらの詳細については、以下のとおりです。
-
決算発表資料の訂正
決算短信等を開示した後に、開示した内容について、変更又は訂正すべき事情が生じた場合に義務付けられている訂正開示をいいます。 -
業績予想の修正・予想値と決算値との差異等
売上高や営業利益、経常利益、当期純利益等について、公表がされた直近の予想値等と比較して、新たに算出した予想値または決算における数値に一定以上の差異が生じた場合に義務付けられている開示をいいます。 -
配当予想・配当予想の修正
公表がされた直近の配当の予想値と比較して、新たに算出した予想値に差異が生じた場合を含め、剰余金の配当について予想値を算出した場合に義務付けられている開示をいいます。
また、上記の決算短信の訂正開示等が、ファンダメンタル情報(stock_fin)の変更を伴い、かつ、次に挙げる条件を全て満たす場合、これも予測対象に含まれます。
E)直近の決算期末または四半期期末に係る決算短信に対する訂正開示等であること
F) 2021年3月27日から同年5月15日までの期間に開示されていること
G) 訂正開示等の開示日及び同日から起算して20営業日を経過した日までの期間、当該開示に対する訂正開示等が行われていないこと
H) 訂正開示等の開示日及び同日から起算して20営業日を経過した日までの期間、上場廃止になっていないこと
なお、ある同一銘柄について、これらの条件を満たす決算短信が複数存在する場合は、最も新しく開示されたもののみを予測の対象とします。
(追記:予測対象期間の20営業日の全てにおいて、株価が存在しない銘柄は、評価の対象外とします。)
以上を踏まえ、各決算短信等(訂正開示等を含みます。)が予測対象に該当するかどうかの事例を、図に示します。
2.1.3. 評価方法
本コンペティションでは、モデルの予測と真の値(決算短信の開示後から起算して20営業日以内に発生する最高値及び最安値)との順位相関係数(算出式1)による定量評価方法を採用します。
先ず、最高値もしくは最安値への変化率について、(算出式1)を用いてそれぞれスピアマンの順位相関係数を計算します。
(算出式1)順位相関係数の計算

d = 対応するXとYの値の順位の差
n = 値のペアの数
dのXとYは、
X = 該当期間の決算日に対して出力されたモデルのスコア(予測値)
Y = 決算短信の開示後から起算して20営業日以内に発生した最高値もしくは最安値への変化率
(式は一部英語Wikipediaスピアマンの順位相関係数より引用 https://en.wikipedia.org/wiki/Spearman%27s_rank_correlation_coefficient)
その上で、それぞれの順位相関係数を以下の(算出式2)を用いて算出した統合スコアを最終スコアとして評価します。
なお、最終スコアは0~8の値をとり、精度が高いほど 小さな値 となります。
(ただし、予測対象期間の20営業日の全てにおいて、株価が存在しない銘柄は、評価の対象外とします。)
(算出式2)最終スコアの計算
P_high : 最高値の順位相関係数
P_low : 最安値の順位相関係数
今回、順位相関係数を採用する理由としては、以下の説明にもあるとおり、金融商品の価格変動の変化率の分布は必ずしも正規分布になるとは限りません。 そのため、本コンペティションでは、特定の分布を仮定しない順位相関係数を採用しています。
一定間隔刻みで集計した騰落率の度数(頻度)分布が、騰落率の平均値を中心軸として左右対称の釣り鐘型の形状になる分布 (正規分布=Normal Distribution) では、「平均値±標準偏差」の範囲に全データの約7割が収まるという確率的な特性を持ちます。ただし、金融商品の価格変動が厳密な意味での正規分布に従うことは実際上ほとんどありません。このため、「平均±標準偏差の範囲に騰落率の約7割が収まる」という考え方は理論的な目安に過ぎなく、発生確率は低いものの標準偏差を大幅に超す価格変動も起こりえます。こうした価格変動のリスクをテールリスクと呼び、とくに、金融市場の混乱期には分布がマイナス方向に偏るケースや、裾が極端に広く厚い"ファット・テール"という現象が確認できます。
(野村証券証券用語解説集より引用 https://www.nomura.co.jp/terms/japan/hi/A02397.html)
本コンペにおいても、例えば新型コロナウイルス感染症 (COVID-19)のような外部影響を受け、マーケットの変化率の分布が歪む期間が存在すると想定されます。したがって、順位相関係数は相関係数と比較して特定の分布を仮定しないことから、本コンペティションにおいては、より適した評価方法であると考えられます。
2.1.4. リーダーボード
一般的に、データ分析コンペティションにおけるリーダーボード(Leaderboard)とは、コンペティション参加者の投稿内容に対する評価(スコア、実行時間等)をランキング形式で並べる表を意味します。本コンペティションで提供するリーダーボードは、パブリックリーダーボード(以下、Public LB)とプライベートリーダーボード(以下、Private LB)の2つで構成されます。以下では、それぞれのリーダーボードの仕様等について説明します。
まず、本コンペティションのPublic LBは、コンペティション開催日より過去の期間を対象として評価を実施します。具体的には、本コンペティションのPublic LBでは、2020年1月1日(水)〜2020年11月30日(月)の期間中に開示された決算短信等を対象に、開示日より起算して20営業日を経過した期間における最高値及び最安値を予測します。
過去の各銘柄の株価は、各Webサイト等で取得可能であることから、本コンペティションのPublic LBではチーティングが容易という特徴があります。そのため。本コンペティションのPublic LBは、他の一般的なPublic LBとは異なり、スコアや実行時間を競うというよりは、モデルが正常に投稿できることを確認するための環境として位置付けられています。
次に、本コンペティションのPrivate LBについて説明します。本コンペティションでは、モデル提出締切日よりも将来のデータを用いて、Private LBを出力します。具体的には、本コンペティションのPrivate LBでは、2021年3月27日(土)〜2021年5月15日(土)に開示された決算短信を対象に、その開示日から起算して20営業日を経過した期間における最高値及び最安値を予測します。
また、この予測に当たっては、決算短信の開示日の期間に応じて5回に分けて実施し、最終的な順位は5回目の評価で決定します。(評価の計算は5回行われますが、最後の1回を除く4回は途中経過をリーダーボードでご確認いただけるように計算しているものになります。)
この5回の評価のスケジュールは次を予定しております。
-
5月10日(月)に3月27日(土)〜4月5日(月)分の財務諸表の評価
-
5月17日(月)に3月27日(土)〜4月12日(月)分の財務諸表の評価
-
5月24日(月)に3月27日(土)〜4月19日(月)分の財務諸表の評価
-
5月31日(月)に3月27日(土)〜4月26日(月)分の財務諸表の評価
-
6月14日(月)に3月27日(土)〜5月15日(土)分の財務諸表の評価
以上を踏まえ、本コンペティションにおけるPublic LBとPrivate LBの概要を、表に示します。
本コンペティションにおけるリーダーボードの仕様
| 項目 | Public LB | Private LB |
|---|---|---|
用途 |
モデルが正常に投稿できることを確認するための環境 |
本コンペティションの最終的なランキングを表示 |
予測対象となる決算短信の開示日の期間 |
2020年1月1日(水)〜2020年11月30日(月) |
2021年3月27日(土)〜2021年5月15日(土) |
予測対象となる決算短信の開示日の条件 |
各銘柄の各四半期ごとに一番開示日が新しい開示 |
2.1.2項に示すとおり |
予測内容 |
決算短信の開示日から起算して20営業日を経過した期間における、各銘柄の最高値及び最安値 |
同左 |
評価方法 |
2.1.3項に示す評価方法 |
2.1.3項に示す評価方法を、5回の決算短信開示期間に応じて実施 |
2.1.5. 決算短信・財務諸表
上場企業の株価は、各社の経営状態等を反映して日々刻々と変化します。そのため、金融商品市場において公正な価格形成と円滑な流通を確保するためには公平で適時、適切な情報開示が必要不可欠なものとなっています。
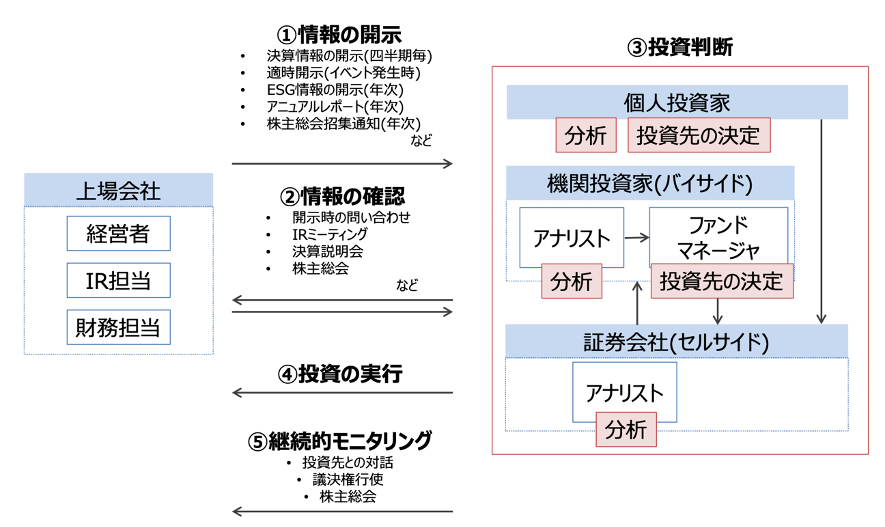
東京証券取引所では、投資者が投資判断を行ううえで必要な会社情報を、迅速、正確かつ公平に提供するための制度として、適時開示制度を設けており、上場企業は、報道機関等を通じてあるいはTDnet(適時開示情報伝達システム)により直接に、広く、かつタイムリーに伝達することという特徴があります。適時開示制度の下で上場企業が開示する資料のことを、適時開示資料と呼びます。適時開示資料とそのメタデータ(タイトル、開示日時等)を総称して適時開示情報と呼び、適時開示情報は「適時開示情報閲覧サービス」で開示されます。下図に投資家における適時開示資料の代表的な用途を示します。
投資家における適時開示資料の代表的な用途
上場企業が開示を義務付けられている適時開示資料の一つに、決算短信があります。決算短信とは、決算発表及び四半期決算発表を行う際に、決算内容の要点をまとめた書類のことです。本資料では、決算発表時に開示する決算短信と、四半期決算発表時に開示する四半期決算短信を総称して、決算短信と呼びます。上場企業は、決算期末を含め四半期毎に決算内容が定まった際、決算内容の開示が義務付けられています。四半期決算短信については、金商法に基づく四半期報告書の法定提出期限が45日とされていることから、また、決算短信については、決算期末後45日以内に決算の内容を開示することを東証が要請していることから、決算短信等の多くは期末後45日以内に開示されています。決算短信の作成要領等は、下記Webサイトで公開されています。
決算短信作成要領・四半期決算短信作成要領 | 日本取引所グループ
https://www.jpx.co.jp/equities/listed-co/format/summary/index.html
決算の内容として開示される決算短信は、大きく、サマリー情報と添付資料で構成されます。
サマリー情報は、投資者の投資判断に重要な影響を与える上場会社の決算の内容について、その要点の一覧性及び比較可能性を確保する観点から、簡潔に取りまとめたものとして、参考様式に基づいて東証が作成を要請している資料です。
添付資料とは、サマリー情報に記載される主要な決算数値を投資者が適切に理解できるようにする目的で作成される、経営成績・財政状態の概況、今後の見通し、財務諸表、主な注記等を記載した資料です。
前述のとおり、決算短信には、財務諸表が添付されています。財務諸表とは、財政状態、経営成績及びキャッシュ・フローの状況を外部の情報利用者に明らかにするためのもので、有価証券届出書や有価証券報告書等に記載される財務計算に関する書類のうち、貸借対照表、損益計算書、株主資本等変動計算書、キャッシュ・フロー計算書の総称を指します。これらの内、貸借対照表、損益計算書、キャッシュ・フロー計算書の3つは、総称して「財務三表」と呼ばれており、上場企業に対する投資判断において特に重要視されています。財務三表の読み方については、下記Webサイトが参考になります。
-
投資に不可欠な財務三表の見方 | 東証マネ部! https://money-bu-jpx.com/news/article022723/
また、各上場企業の決算発表予定日(決算短信の開示予定日)は、下記JPXのWebサイトにて随時公開されています。投資家の投資判断において、各上場企業の決算発表は特に重要視されていることから、当該Webサイトは多くの投資家より注目を集めていると推察されます。
-
決算発表予定日 | 日本取引所グループ https://www.jpx.co.jp/listing/event-schedules/financial-announcement/index.html
以上のとおり、本コンペティションで予測対象の起点となる決算短信には、各上場企業の重要な決算内容が記されています。本コンペティションでは、決算短信に含まれる財務諸表から抽出したファンダメンタル情報をコンペティションページ若しくは専用のAPIにおいて配信しており、これを用いることで株価の先行きを予測していただきます。
2.2. データセットの説明
ここでは、コンペティションで提供している各データについて説明します。提供されるデータは以下の5種類です。
データ概要
| ファイル名 | 説明 |
|---|---|
stock_list |
各銘柄の情報が記録されたデータ |
stock_price |
各銘柄の株価情報(始値・高値・安値・終値等)が記録されたデータ |
stock_fin |
各銘柄のファンダメンタル情報(決算数値データや配当データ等)が記録されたデータ |
stock_fin_price |
データが扱いやすいようにstock_price及びstock_finをマージしたデータ |
stock_labels |
本コンペティションで学習に用いるラベル(目的変数)が記録されたデータ |
提供データについては、2016年1月初から2020年12月末をcsvファイル形式、2021年1月初からのデータについては、本コンペティション専用のAPIにて提供いたします。APIによるデータ取得につきましては、8章をご参照ください。
2.2.1. 銘柄情報: stock_list
stock_listは、銘柄の名前や業種区分などの基本情報が含まれています。発行済株式数は、会社が発行することをあらかじめ定款に定めている株式数(授権株式数)のうち、会社が既に発行した株式数のことです。発行済株式数と株価とかけ合わせて時価総額を計算することができます。時価総額は企業価値を評価する際に用いられる重要な指標です。業種区分情報は、マーケットにおける業種別の平均などを計算する時に役立つ情報です。33業種は証券コード協議会が定めており、17業種はTOPIX-17シリーズとして「投資利便性を考慮して17業種に再編したもの」(JPX東証33業種別株価指数・TOPIX-17シリーズファクトシートより引用 https://www.jpx.co.jp/markets/indices/line-up/index.html) です。
「業種」(JPX用語集より引用 https://www.jpx.co.jp/glossary/ka/112.html)
| 変数名 | 説明 | 型 | 例 |
|---|---|---|---|
prediction_target |
予測対象銘柄 |
bool |
True |
Effective Date |
銘柄情報の基準日 |
int64 |
20201030 |
Local Code |
株式銘柄コード |
int64 |
1301 |
Name (English) |
銘柄名 |
object |
KYOKUYO CO.,LTD. |
Section/Products |
市場・商品区分 |
object |
First Section (Domestic) |
33 Sector(Code) |
銘柄の33業種区分(コード) |
int64 |
50 |
33 Sector(name) |
銘柄の33業種区分(名前) |
object |
Fishery, Agriculture and Forestry |
17 Sector(Code) |
銘柄の17業種区分(コード) |
int64 |
1 |
17 Sector(name) |
銘柄の17業種区分(名前) |
object |
FOODS |
Size Code (New Index Series) |
TOPIXニューインデックスシリーズ規模区分(コード) |
object |
7 |
Size (New Index Series) |
TOPIXニューインデックスシリーズ規模区分 |
object |
TOPIX Small 2 |
IssuedShareEquityQuote AccountingStandard |
会計基準 単独:NonConsolidated、連結国内:ConsolidatedJP、連結SEC:ConsolidatedUS、連結IFRS:ConsolidatedIFRS |
object |
ConsolidatedJP |
IssuedShareEquityQuote ModifyDate |
更新日 |
object |
2020/11/06 |
IssuedShareEquityQuote IssuedShare |
発行済株式数 |
float64 |
10928283.0 |
(JPX東証上場銘柄一覧より引用 https://www.jpx.co.jp/markets/statistics-equities/misc/01.html)
(Quick xignite API Market Data API Catalogより引用 https://www.marketdata-cloud.quick-co.jp/Products/)

2.2.2. 株価情報 : stock_price
stock_priceには各銘柄の各日付の始値や終値などの株価情報が記録されています。テクニカル分析などで終値ベースの分析を実施する場合は、ExchangeOfficialCloseを利用します。
ここでいうテクニカル分析というのは、マーケットデータから計算される指標に基づいた分析のことです。また、終値ベースの分析とは、マーケットデータの中でも、終値のみを用いた分析を表しています。
株価情報は、「株式分割」や「株式併合」が発生した際に生じる株価の変動を、株式数の変化率に応じて調整されています。特徴量の定義によっては、その日付時点で実際に取引された株価や出来高を取得したい場合がありますが、その場合は累積調整係数を使用して
[調整前株価] = [調整済株価] * [累積調整係数] 及び [調整前出来高] = [調整済出来高] / [累積調整係数]
という計算で算出可能です。
「株式分割」(JPX用語集より引用 https://www.jpx.co.jp/glossary/ka/81.html)
「株式併合」(JPX用語集より引用 https://www.jpx.co.jp/glossary/ka/83.html)
ただし、これらの特徴量をモデルに使用する場合には注意が必要です。
履歴データの累積調整係数は過去のある日時点では知り得ない未来の情報を含んでいることに注意する必要があります。具体的には、過去のある日時点の累積調整係数が2である場合、その日以降に1:2の株式分割が発生していることがわかります。
一般に株式分割は流動性向上を期待できるポジティブなイベントとみなされています。仮に、モデル学習時に累積調整係数をモデルへ入力し、モデルが累積調整係数が大きい銘柄は未来の株価が上がる傾向があるということを学習し、履歴データを使用したバックテストでは良い結果がでたとします。しかし、このモデルに最新データを入力して予測を出力した場合、その予測は期待する結果を得られない可能性があります。なぜなら、最新データの累積調整係数にはまだ発生していない未来の情報は含まれていないためです。
このように、その日付時点では取得できない未来の情報をモデルに入力することをリークといい、時系列データには累積調整係数のようにその日付時点では取得できない情報が含まれていることがあるため、リークにはとくに注意する必要があります。
データの特性
-
マーケットが開いている日に取引が成立しなかった銘柄は、売買高が0となり、四本値 (始値、高値、安値、終値) 全てが0と表示されます。
-
stock_priceのデータは、そのデータに含まれている最新日付時点で累積調整係数1となるように調整されます。調整済み株価についても同様に過去に遡って更新されます。
| 変数名 | 説明 | 型 | 例 |
|---|---|---|---|
Local Code |
銘柄コード |
int64 |
1301 |
EndOfDayQuote Date |
日付 |
object |
2016/01/04 |
EndOfDayQuote Open |
始値 |
float64 |
2800 |
EndOfDayQuote High |
高値 |
float64 |
2820 |
EndOfDayQuote Low |
安値 |
float64 |
2740 |
EndOfDayQuote Close |
終値。大引け後にセットされる |
float64 |
2750 |
EndOfDayQuote ExchangeOfficialClose |
取引所公式終値。最終の特別気配または最終気配を含む終値 |
float64 |
2750 |
EndOfDayQuote Volume |
売買高 |
float64 |
32000 |
EndOfDayQuote CumulativeAdjustmentFactor |
累積調整係数 |
float64 |
0.1 |
EndOfDayQuote PreviousClose |
前回の終値 |
float64 |
2770 |
EndOfDayQuote PreviousCloseDate |
前回の終値が発生した日 |
object |
2015/12/30 |
EndOfDayQuote PreviousExchangeOfficialClose |
前回の取引所公式終値 |
float64 |
2770 |
EndOfDayQuote PreviousExchangeOfficialCloseDate |
前回の取引所公式終値が発生した日 |
object |
2015/12/30 |
EndOfDayQuote ChangeFromPreviousClose |
騰落幅。前回終値と直近約定値の価格差 |
float64 |
-20 |
EndOfDayQuote PercentChangeFromPreviousClose |
騰落率。前回終値からの直近約定値の上昇率または下落率 |
float64 |
-0.722 |
EndOfDayQuote VWAP |
売買高加重平均価格(VWAP) |
float64 |
2778.25 |
(Quick xignite API Market Data API Catalogより引用 https://www.marketdata-cloud.quick-co.jp/Products/)

2.2.3. ファンダメンタル情報: stock_fin
株式投資における ファンダメンタル情報 とは、対象銘柄の純資産といった財務状況や当期純利益といった業績状況を表す情報のことです。ファンダメンタル情報を用いて、各銘柄の成長性、収益性、安全性、割安度などの投資判断に活用することができます。ファンダメンタル情報を利用した解析は、さまざまな手法が考案されています。
ファンダメンタル情報のデータセットであるstock_finにおいて、いくつかの変数名は Forecast から始まっていますが、これらは各企業が来期の自社の業績・財務状況を予想したデータです。例えば、企業が来期の業績が厳しいことが予め分かっている場合には、予想として早めに開示することがあるため、予想のデータも重要な可能性があります。
| 変数名 | 説明 | 型 | 例 |
|---|---|---|---|
base_date |
日付 |
object |
2016/01/04 |
Local Code |
銘柄コード |
int64 |
2753 |
Result_FinancialStatement AccountingStandard |
会計基準 単独:NonConsolidated、連結国内:ConsolidatedJP、連結SEC:ConsolidatedUS、連結IFRS:ConsolidatedIFRS |
object |
ConsolidatedJP |
Result_FinancialStatement FiscalPeriodEnd |
決算期 |
object |
2015/12 |
Result_FinancialStatement ReportType |
決算種別 第1四半期:Q1、中間決算:Q2、第3四半期:Q3、本決算:Annual |
object |
Q3 |
Result_FinancialStatement FiscalYear |
決算年度。本決算の決算期末が属する年。 |
float64 |
2016 |
Result_FinancialStatement ModifyDate |
更新日 |
object |
2016/01/04 |
Result_FinancialStatement CompanyType |
会社区分 一般事業会社:GB、銀行:BK、証券会社:SE、損保会社:IN ※上記に該当しない場合は空文字を設定してます。 |
object |
GB |
Result_FinancialStatement ChangeOfFiscalYearEnd |
決算期変更フラグ 決算期変更あり:true、決算期変更なし:false |
object |
False |
Result_FinancialStatement NetSales |
売上高(単位:百万円) 会社区分によって項目名の読替えを行ういます。 銀行:経常収益、証券:営業収益、損保:経常収益 ※未開示の場合は空文字を設定してます。 |
float64 |
22354 |
Result_FinancialStatement OperatingIncome |
営業利益(単位:百万円) ※未開示の場合は空文字を設定してます。 |
float64 |
2391 |
Result_FinancialStatement OrdinaryIncome |
経常利益(単位:百万円) 会計基準が連結SECの場合は、項目名を「税引前利益」に読み替えます。 ※未開示の場合は空文字を設定してます。 |
float64 |
2466 |
Result_FinancialStatement NetIncome |
当期純利益(単位:百万円) ※未開示の場合は空文字を設定してます。 |
float64 |
1645 |
Result_FinancialStatement TotalAssets |
総資産(単位:百万円) ※未開示の場合は空文字を設定してます。 |
float64 |
21251 |
Result_FinancialStatement NetAssets |
純資産(単位:百万円) ※未開示の場合は空文字を設定してます。 |
float64 |
16962 |
Result_FinancialStatement CashFlowsFromOperatingActivities |
営業キャッシュフロー(単位:百万円) ※未開示の場合は空文字を設定してます。 |
float64 |
12404 |
Result_FinancialStatement CashFlowsFromFinancingActivities |
財務キャッシュフロー(単位:百万円) ※未開示の場合は空文字を設定してます。 |
float64 |
-98 |
Result_FinancialStatement CashFlowsFromInvestingActivities |
投資キャッシュフロー(単位:百万円) ※未開示の場合は空文字を設定してます。 |
float64 |
-1307 |
Forecast_FinancialStatement AccountingStandard |
予想: 会計基準 単独:NonConsolidated、連結国内:ConsolidatedJP、連結SEC:ConsolidatedUS、連結IFRS:ConsolidatedIFRS |
object |
ConsolidatedJP |
Forecast_FinancialStatement FiscalPeriodEnd |
来期予想情報: 決算期 |
object |
2016/03 |
Forecast_FinancialStatement ReportType |
来期予想情報: 決算種別 第1四半期:Q1、中間決算:Q2、第3四半期:Q3、本決算:Annual |
object |
Annual |
Forecast_FinancialStatement FiscalYear |
来期予想情報: 決算年度。本決算の決算期末が属する年。 |
float64 |
2016 |
Forecast_FinancialStatement ModifyDate |
来期予想情報: 更新日 |
object |
2016/01/04 |
Forecast_FinancialStatement CompanyType |
来期予想情報: 会社区分 一般事業会社:GB、銀行:BK、証券会社:SE、損保会社:IN ※上記に該当しない場合は空文字を設定してます。 |
object |
GB |
Forecast_FinancialStatement ChangeOfFiscalYearEnd |
来期予想情報: 決算期変更フラグ 決算期変更あり:true、決算期変更なし:false |
object |
False |
Forecast_FinancialStatement NetSales |
来期予想情報: 売上高(単位:百万円) 会社区分によって項目名の読替えを行います。 銀行:経常収益、証券:営業収益、損保:経常収益 ※未開示の場合は空文字を設定してます。 |
float64 |
30500 |
Forecast_FinancialStatement OperatingIncome |
来期予想情報: 営業利益(単位:百万円) ※未開示の場合は空文字を設定してます。 |
float64 |
3110 |
Forecast_FinancialStatement OrdinaryIncome |
来期予想情報: 経常利益(単位:百万円) 会計基準が連結SECの場合は、項目名を「税引前利益」に読み替えます。 ※未開示の場合は空文字を設定してます。 |
float64 |
3200 |
Forecast_FinancialStatement NetIncome |
来期予想情報: 当期純利益(単位:百万円) ※未開示の場合は空文字を設定してます。 |
float64 |
2130 |
Result_Dividend FiscalPeriodEnd |
配当情報: 決算期 |
object |
2015/11 |
Result_Dividend ReportType |
配当情報: 決算種別 第1四半期:Q1、中間決算:Q2、第3四半期:Q3、本決算:Annual |
object |
Annual |
Result_Dividend FiscalYear |
配当情報: 決算年度。本決算の決算期末が属する年。 |
float64 |
2015 |
Result_Dividend ModifyDate |
配当情報: 更新日 |
object |
2016/01/07 |
Result_Dividend RecordDate |
配当情報: 配当基準日 |
object |
2015/11/30 |
Result_Dividend DividendPayableDate |
配当情報: 配当支払開始日 ※予想の場合は空文字を設定してます。 |
object |
2016/02/29 |
Result_Dividend QuarterlyDividendPerShare |
配当情報: 一株当たり四半期配当金(単位:円) ※未開示の場合は空文字を設定してます。 |
float64 |
8 |
Result_Dividend AnnualDividendPerShare |
配当情報: 一株当たり年間配当金累計(単位:円)※未開示の場合は空文字を設定してます。 |
float64 |
15 |
Forecast_Dividend FiscalPeriodEnd |
予想配当情報: 決算期 |
object |
2016/03 |
Forecast_Dividend ReportType |
予想配当情報: 決算種別 第1四半期:Q1、中間決算:Q2、第3四半期:Q3、本決算:Annual |
object |
Annual |
Forecast_Dividend FiscalYear |
予想配当情報: 決算年度。本決算の決算期末が属する年。 |
float64 |
2016 |
Forecast_Dividend ModifyDate |
予想配当情報: 更新日 |
object |
2016/01/04 |
Forecast_Dividend RecordDate |
予想配当情報: 配当基準日 |
object |
2016/03/31 |
Forecast_Dividend QuarterlyDividendPerShare |
予想配当情報: 一株当たり四半期配当金(単位:円) ※未開示の場合は空文字を設定してます。 |
float64 |
45 |
Forecast_Dividend AnnualDividendPerShare |
予想配当情報: 一株当たり年間配当金累計(単位:円)※未開示の場合は空文字を設定してます。 |
float64 |
90 |
(Quick xignite API Market Data API Catalogより引用 https://www.marketdata-cloud.quick-co.jp/Products/)

2.2.4. 財務諸表+株価情報: stock_fin_price
stock_fin_priceは、株価情報である<<株価情報 : stock_price, stock_price>>と財務諸表である<<ファンダメンタル情報: stock_fin, stock_fin>>をデータとして扱いやすいように結合したデータです。変数名や型などについては、同じであるため記載を省略しています。
また、データのサイズが非常に大きいため、必要に応じて活用していただきたいと思います。
2.2.5. 目的変数: stock_labels
stock_labelsは予測の目的変数のデータであり、各銘柄で決算発表が行われた日の取引所公式終値から、その日の翌営業日以降N(5,10,20)営業日間における最高値及び最安値への変化率を記録したデータです。
各値の計算式は、 ([基準日付の翌日以降N営業日間における高値/安値] / [基準日付の終値]) - 1 です。
なお、ラベルの対象期間 (5、10、20営業日の間) に値が付かなかった場合は、ラベルを NaN としております。
| 変数名 | 説明 | 型 | 例 |
|---|---|---|---|
base_date |
基準日付(各銘柄で決算短信等の開示がされた日) |
object |
2016-01-04 |
Local Code |
銘柄コード |
int64 |
1301 |
label_date_5 |
基準日付から5営業日後の日付。label_high_5算出に使用される終値範囲の基準日 |
object |
2016-01-12 |
label_high_5 |
基準日付の終値から5営業日の間の最高値への変化率 |
float64 |
0.00364 |
label_low_5 |
基準日付の終値から5営業日の間の最安値への変化率 |
float64 |
-0.04 |
label_date_10 |
基準日付から10営業日後の日付。label_high_10算出に使用される終値範囲の基準日 |
object |
2016-01-19 |
label_high_10 |
基準日付の終値から10営業日の間の最高値への変化率 |
float64 |
0.00364 |
label_low_10 |
基準日付の終値から10営業日の間の最安値への変化率 |
float64 |
-0.05455 |
label_date_20 |
基準日付から20営業日後の日付。label_high_20算出に使用される終値範囲の基準日 |
object |
2016-02-02 |
label_high_20 |
基準日付の終値から20営業日の間の最高値への変化率 |
float64 |
0.00364 |
label_low_20 |
基準日付の終値から20営業日の間の最安値への変化率 |
float64 |
-0.08364 |

2.3. 実行環境及び必要なライブラリ
2.3.1. 実行環境
本チュートリアルの実行環境は、本コンペティションで提出するモデルの実行環境と同一環境とするために以下のpython環境を用います。環境構築方法について、詳しくは SIGNATE: Runtime 投稿方法: ローカル開発環境の構築方法は? をご参照ください。
anaconda3-2019.03
2.3.2. Google Colaboratoryの利用
本章はDockerを用いた実行環境の利用を想定して記述しておりますが、Dockerの実行環境構築がご利用のOSなど何らかの理由により困難な方、より簡便にチュートリアルを実行したい方はGoogle Colaboratoryの利用をご検討ください。本チュートリアルで提供されるNotebookはGoogle Colaboratoryでも実行可能です。詳細は第7章をご参照ください。
2.3.3. Dockerを用いた実行環境構築方法
本チュートリアルのリポジトリを git clone していただき、以下の手順を実行していただくことで実行環境のdockerコンテナ内でjupyter notebookを起動可能となっています。 Chapter02 ディレクトリ内には、本チュートリアルのコードを記載した ipynb ファイルを配置しておりますので必要に応じてご活用ください。
Windows環境の場合、コマンド実行には「PowerShell」などをご使用ください。なお、PowerShellの利用に当たっては、最新のセキュリティ事情を踏まえご自身でご判断ください。
docker のインストールについては http://docs.docker.jp/get-docker.html をご参照ください。docker の制約としてマウントするパスにはアルファベット、数字、「_」、「.」、「-」以外の文字を使用するとエラーとなることがあるようです。その場合は、パスが前述の文字のみで構成されているディレクトリをご使用ください。
cd handson/
# データ配置先のディレクトリを作成
mkdir data_dir
# その後作成したhandson/data_dirに、コンペティションサイトよりデータをダウンロードし配置します。
# dockerでjupyter notebookを起動します。(初回実行時は約2GB程度コンテナイメージをダウンロードします。)
# データ配置先のディレクトリを /path/to としてマウントしています。
# 学習済みモデル提出用のディレクトリ (handson/Chapter02/archive) を /opt/ml としてマウントしています。
# jupyter notebook作業用に handson ディレクトリを /notebook としてマウントしています。
# jupyter notebook は port 8888でtokenとpasswordを空にして、vscode のjupyter pluginからアクセスできるように xsrf 対策を無効化しています。
docker run --name tutorial -v ${PWD}/data_dir:/path/to -v ${PWD}/Chapter02/archive:/opt/ml -v ${PWD}:/notebook -e PYTHONPATH=/opt/ml/src -p8888:8888 --rm -it continuumio/anaconda3:2019.03 jupyter notebook --ip 0.0.0.0 --allow-root --no-browser --no-mathjax --NotebookApp.disable_check_xsrf=True --NotebookApp.token='' --NotebookApp.password='' /notebook
# ブラウザで以下のURLにアクセスしてjupyter notebookの画面が表示されていて、本チュートリアル用のnotebookが表示されていることを確認します。
http://localhost:8888/2.3.4. 必要なライブラリのインストール
本チュートリアル内では、上記の実行環境に含まれていないライブラリを使用するため、以下のコマンドを使用して個別にインストールします。
# shap用にg++とgccをインストールします
apt-get update
apt-get install -y --no-install-recommends g++ gcc
# 必要なライブラリをインストールします
pip install shap==0.37.0 slicer==0.0.3 xgboost==1.3.0.post02.3.5. ライブラリの読み込み
本チュートリアルでは、下記のライブラリのインポートを行います。
import os
import pickle
import sys
import warnings
from glob import glob
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import shap
import xgboost
from scipy.stats import spearmanr
from sklearn.ensemble import (
ExtraTreesRegressor,
GradientBoostingRegressor,
RandomForestRegressor,
)
from sklearn.metrics import accuracy_score, mean_squared_error
from tqdm.auto import tqdm
# 表示用の設定を変更します
%matplotlib inline
pd.options.display.max_rows = 100
pd.options.display.max_columns = 100
pd.options.display.width = 1202.3.6. ライブラリ解説
| ライブラリ名 | 目的 | 公式ドキュメント | 入門解説 q |
|---|---|---|---|
pandas |
データの処理 |
||
numpy |
データの処理 |
||
glob |
ファイルの検知 |
||
tqdm |
計算の進捗確認 |
||
sklearn |
機械学習モデルを作成 |
||
matplotlib |
データの可視化 |
||
scipy |
統計用のライブラリ |
||
seaborn |
データの可視化 |
||
shap |
SHAP分析 |
||
xgboost |
機械学習モデル |
2.3.7. 実行環境の確認
pythonのバージョンが3.7.3であることを確認します。
print(sys.version)出力
3.7.3 (default, Mar 27 2019, 22:11:17)
[GCC 7.3.0]2.4. データセットの読み込み
本コンペティション用に提供されているデータセットをダウンロードして、ファイルを解凍した場所を定義します。
# データセット保存先ディレクトリ(""の中身はご自身の環境に合わせて定義してください。)
dataset_dir="/path/to"データを読み込みます。なお、本チュートリアルでは stock_fin 及び stock_price を使用するため、 stock_fin_price は読み込まずに進めます。
# 読み込むファイルを定義します。
inputs = {
"stock_list": f"{dataset_dir}/stock_list.csv.gz",
"stock_price": f"{dataset_dir}/stock_price.csv.gz",
"stock_fin": f"{dataset_dir}/stock_fin.csv.gz",
# 本チュートリアルでは使用しないため、コメントアウトしています。
# "stock_fin_price": f"{dataset_dir}/stock_fin_price.csv.gz",
"stock_labels": f"{dataset_dir}/stock_labels.csv.gz",
}
# ファイルを読み込みます
dfs = {}
for k, v in inputs.items():
print(k)
dfs[k] = pd.read_csv(v)
# DataFrameのindexを設定します。
if k == "stock_price":
dfs[k].loc[:, "datetime"] = pd.to_datetime(
dfs[k].loc[:, "EndOfDayQuote Date"]
)
dfs[k].set_index("datetime", inplace=True)
elif k in ["stock_fin", "stock_fin_price", "stock_labels"]:
dfs[k].loc[:, "datetime"] = pd.to_datetime(
dfs[k].loc[:, "base_date"]
)
dfs[k].set_index("datetime", inplace=True)読み込んだデータを確認します。
for k in inputs.keys():
print(k)
print(dfs[k].info())
print(dfs[k].head(1).T)2.5. データセットの可視化
データセットの各項目の特徴を把握することは、モデルを作成する上で重要な要素の1つです。一般にデータの特徴を把握するためには、各項目の意味を把握し、値の平均や標準偏差などの基本統計量を確認します。可視化もそういった特徴把握の手法の1つで、データをグラフなどで表現することで特性を直感的に理解できるようになります。
Chapter 2.2 データセットの説明では、本コンペで用いるデータセットについて説明しました。ここではそれらのデータを、 matplotlib と seaborn を用いて可視化します。財務諸表、株価、移動平均、価格変化率、ヒストリカル・ボラティリティを個別で見て、最後に1つのグラフとしてまとめて可視化します。
2.5.1. 財務諸表
ファンダメンタル情報は項目が多いため、今回は、売上高、営業利益、純利益、純資産及びその決算期の間の関係について可視化します。サンプルとして、銘柄コード9984の「ソフトバンクグループ」を可視化します。
# stock_finの読み込み
fin = dfs["stock_fin"]
# 銘柄コード9984にデータを絞る
code = 9984
fin_data = fin[fin["Local Code"] == code]
# 2019年までの値を表示
fin_data = fin_data[:"2019"]
# プロット対象を定義
columns = [
"Result_FinancialStatement NetSales", # 売上高
"Result_FinancialStatement OperatingIncome", # 営業利益
"Result_FinancialStatement NetIncome", # 純利益
"Result_FinancialStatement NetAssets", # 純資産
"Result_FinancialStatement ReportType" # 決算期
]
# プロット
sns.pairplot(fin_data[columns], hue="Result_FinancialStatement ReportType", height=5)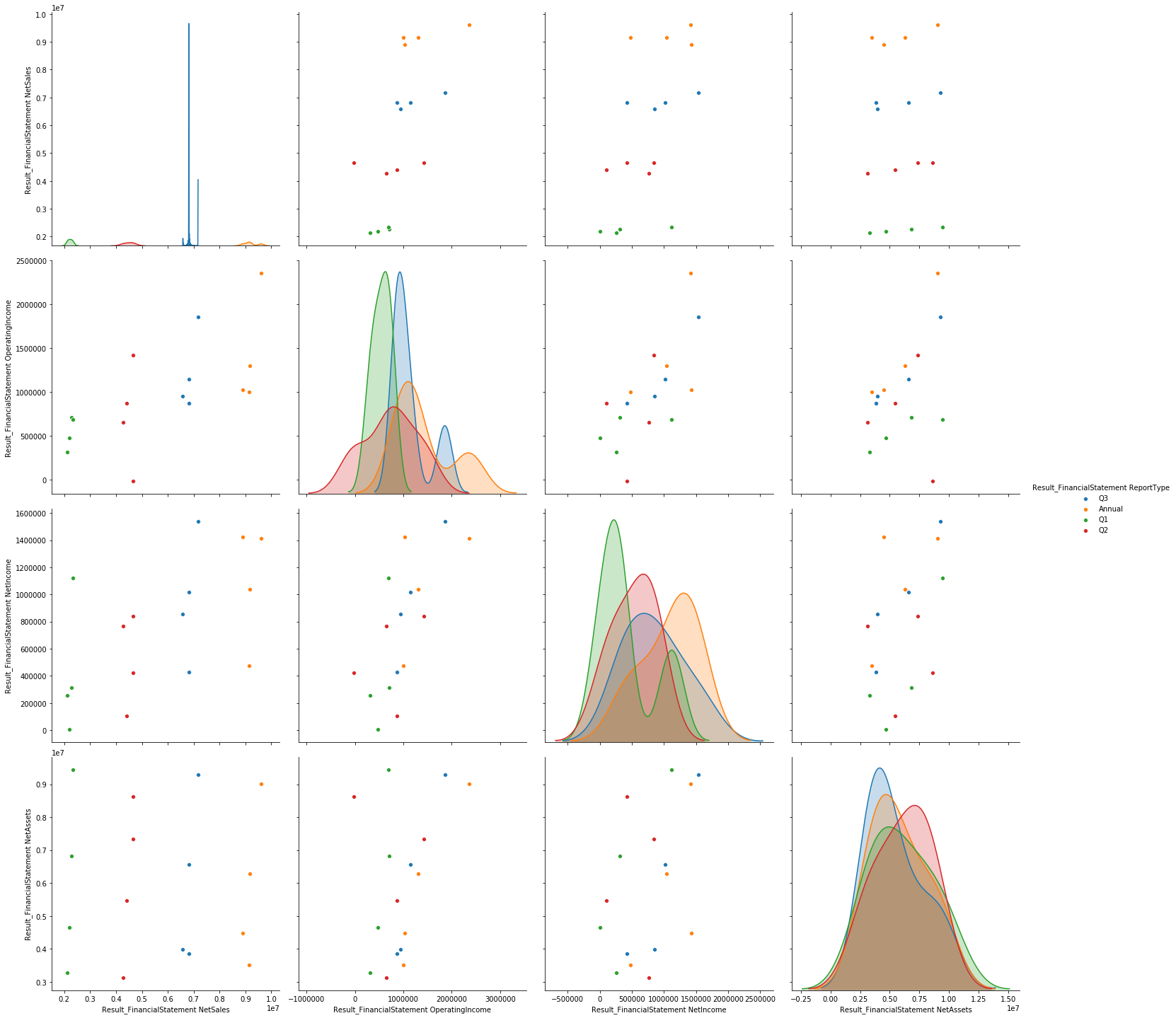
上記のプロットについて説明しますと、各色(緑、赤、青、オレンジ)はそれぞれQ1,Q2,Q3,Annualにおける決算の値に対応しており、対角に並んでいるプロットは各軸の特徴量の分布を表しています。また、その他のプロットは、各軸2つの変数の散布図を表しています。
例えば、2行1列目のグラフを見ると、横軸が売上高、縦軸が営業利益になっています。高い売上高は高い営業利益に繋がっています。また、決算期がQ1からQ3,本決算に至るまでに基本的に右肩上がりであることが分かります。このことから財務データの純売上高や営業利益などの変数は、各決算期ごとの値ではなく、各決算期を積み上げ式で記録されていると推測できます。
複数銘柄のファンダメンタル情報の比較
# stock_finの読み込み
fin = dfs["stock_fin"]
# 銘柄コード9984と9983を比較する
codes = [9984, 9983]
multi_df = dict()
# プロット対象を定義
columns = [
"Result_FinancialStatement NetSales", # 売上高
"Result_FinancialStatement OperatingIncome", # 営業利益
"Result_FinancialStatement NetIncome", # 純利益
"Result_FinancialStatement NetAssets", # 純資産
"Result_FinancialStatement ReportType" # 決算期
]
# 比較対象の銘柄コード毎に処理
for code in codes:
# 特定の銘柄コードに絞り込み
fin_data = fin[fin["Local Code"] == code]
# 2019年までの値を表示
fin_data = fin_data[:"2019"].copy()
# 重複を排除
fin_data.drop_duplicates(
subset=[
"Local Code",
"Result_FinancialStatement FiscalYear",
"Result_FinancialStatement ReportType"
],
keep="last", inplace=True)
# プロット対象のカラムを取得
_fin_data = fin_data[columns]
# 決算期毎の平均を取得
multi_df[code] = _fin_data[columns].groupby("Result_FinancialStatement ReportType").mean()
# 銘柄毎に処理していたものを結合
multi_df = pd.concat(multi_df)
# 凡例を調整
multi_df.set_index(multi_df.index.map(lambda t: f"{t[0]}/{t[1]}"), inplace=True)
# プロット
ax = multi_df.T.plot(kind="bar", figsize=(12, 6), grid=True)
# Y軸のラベルを調整
ax.get_yaxis().set_major_formatter(matplotlib.ticker.FuncFormatter(lambda x, p: "{} bYen".format(int(x / 1_000))))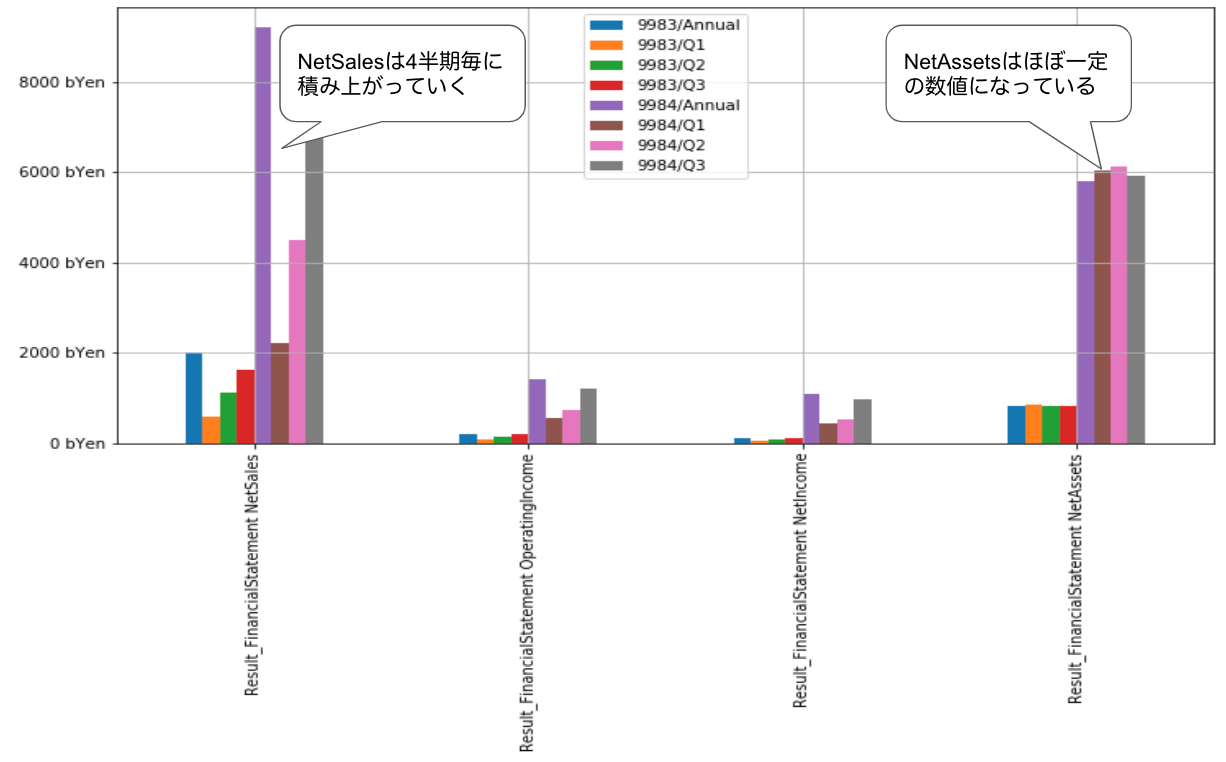
画像の中にコメントを記載しておりますが、NetSales(売上高)とNetAssets(純資産)の特性の違いがわかります。NetAssetsは一定の数値になっており、決算期の影響をあまり受けていないことがわかります。一方、NetSalesはQ1からAnnualにかけて数値が積み上がっており、Q1から決算期が進むごとに大きくなる特性を持つことがわかります。
2.5.2. 株価
ここでは、サンプルとして銘柄コード9984の「ソフトバンクグループ」の終値の動きを可視化します。
# stock_priceの読み込み
price = dfs["stock_price"]
# 特定の銘柄コードに絞り込み
code = 9984
price_data = price[price["Local Code"] == code]
# 2019年までの値を表示
price_data = price_data[:"2019"]
# プロット
fig, ax = plt.subplots(figsize=(20, 8))
ax.plot(price_data["EndOfDayQuote ExchangeOfficialClose"], label=f"securities code : {code}.T")
ax.set_ylabel("stock_price")
ax.set_xlabel("datetime")
ax.grid(True)
ax.legend()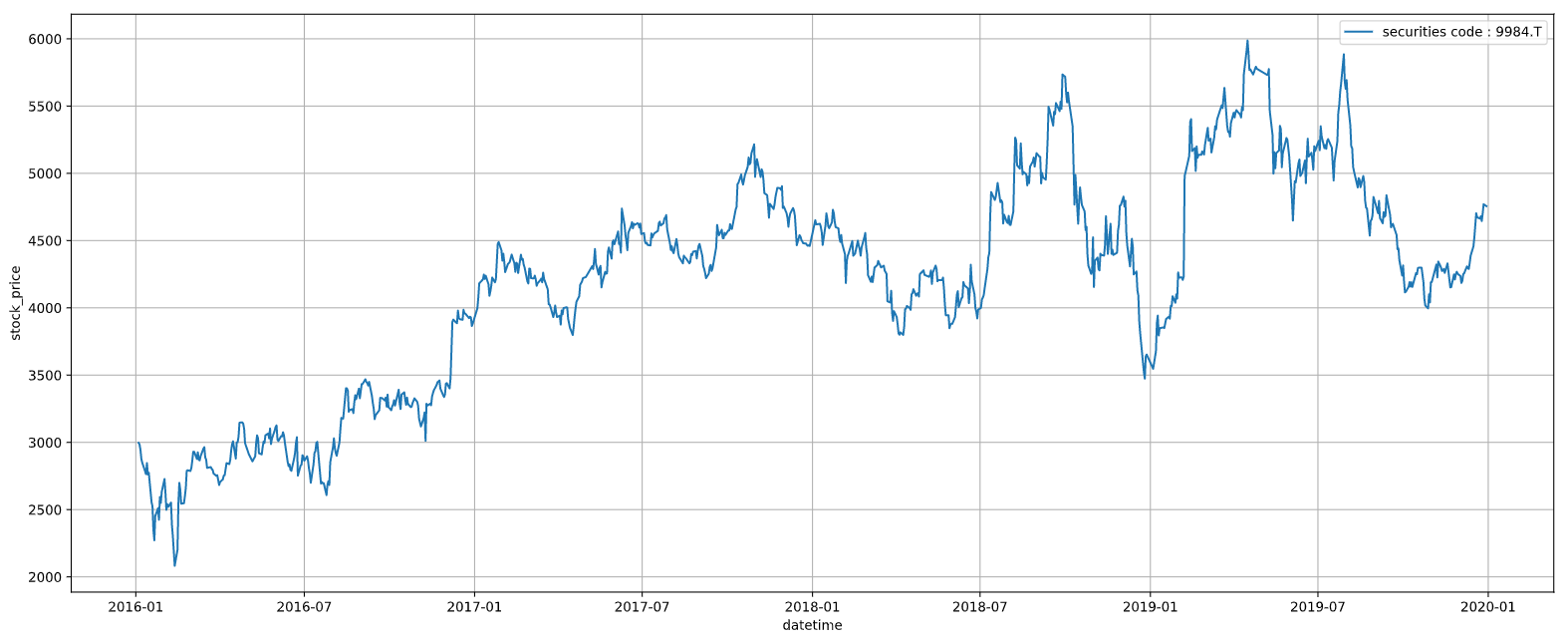
2.5.3. 移動平均
ここでは移動平均をプロットします。移動平均にもさまざまな種類がありますが、ここでは単純移動平均線を用います。単純移動平均線というのは、例えば、5日線であれば、直近5営業日の価格の平均値です。これを1つずつ期間をスライドしながら計算したものになります。
# stock_priceの読み込み
price = dfs["stock_price"]
# 特定の銘柄コードに絞り込み
code = 9984
price_data = price[price["Local Code"] == code]
# 2019年までの値を表示
price_data = price_data[:"2019"].copy()
# 5日、25日、75日の移動平均を算出
periods = [5, 25, 75]
cols = []
for period in periods:
col = "{} windows simple moving average".format(period)
price_data[col] = price_data["EndOfDayQuote ExchangeOfficialClose"].rolling(period, min_periods=1).mean()
cols.append(col)
# プロット
fig, ax = plt.subplots(figsize=(20, 8))
for col in cols:
ax.plot(price_data[col], label=col)
ax.set_ylabel("stock_price")
ax.set_xlabel("datetime")
ax.grid(True)
ax.legend()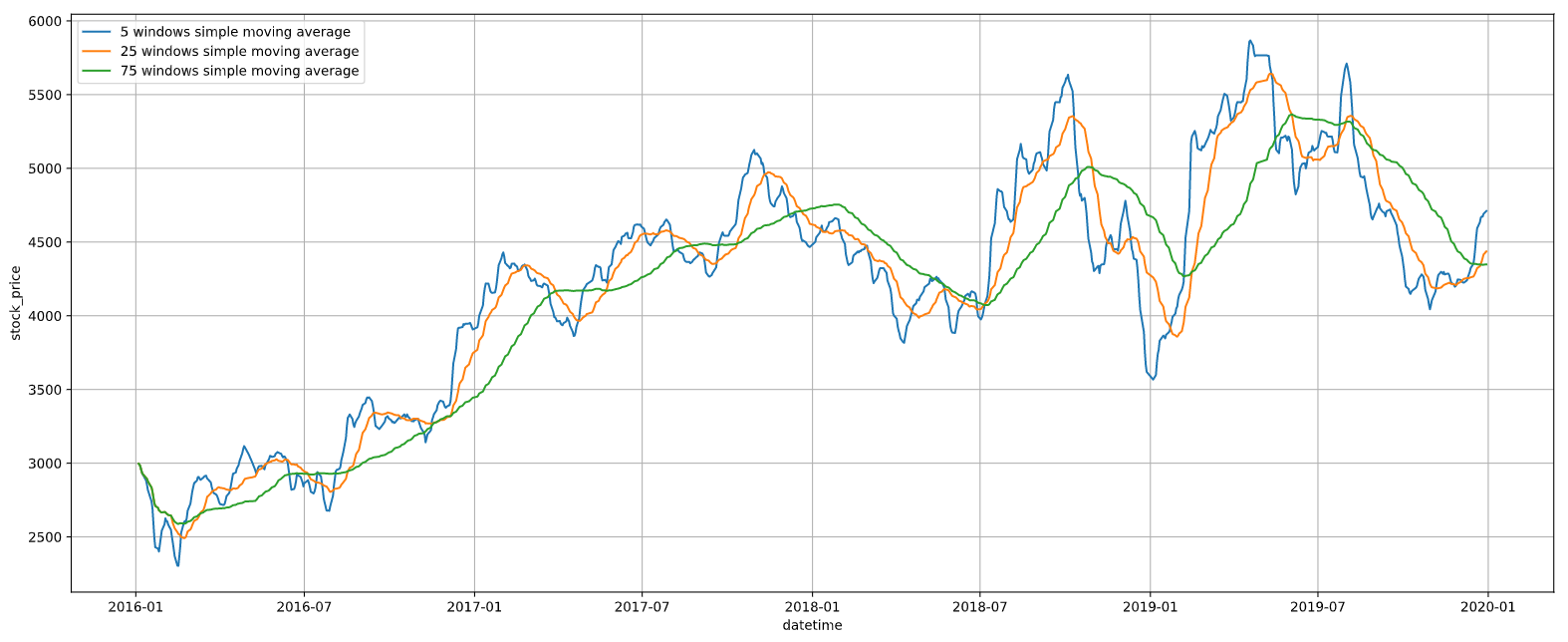
2.5.4. 価格変化率
価格変化率は、価格がその期間でどれくらい変化したかを(%)で表現したものです。相場の勢いや方向性等を判断する際によく使われます。
# stock_priceの読み込み
price = dfs["stock_price"]
# 特定の銘柄コードに絞り込み
code = 9984
price_data = price[price["Local Code"] == code]
# 2019年までの値を表示
price_data = price_data[:"2019"].copy()
# 5日、25日、75日の価格変化率を算出
periods = [5, 25, 75]
cols = []
for period in periods:
col = "{} windows rate of return".format(period)
price_data[col] = price_data["EndOfDayQuote ExchangeOfficialClose"].pct_change(period) * 100
cols.append(col)
# プロット
fig, ax = plt.subplots(figsize=(20, 8))
for col in cols:
ax.plot(price_data[col], label=col)
ax.set_ylabel("rate of return (%)")
ax.set_xlabel("datetime")
ax.grid(True)
ax.legend()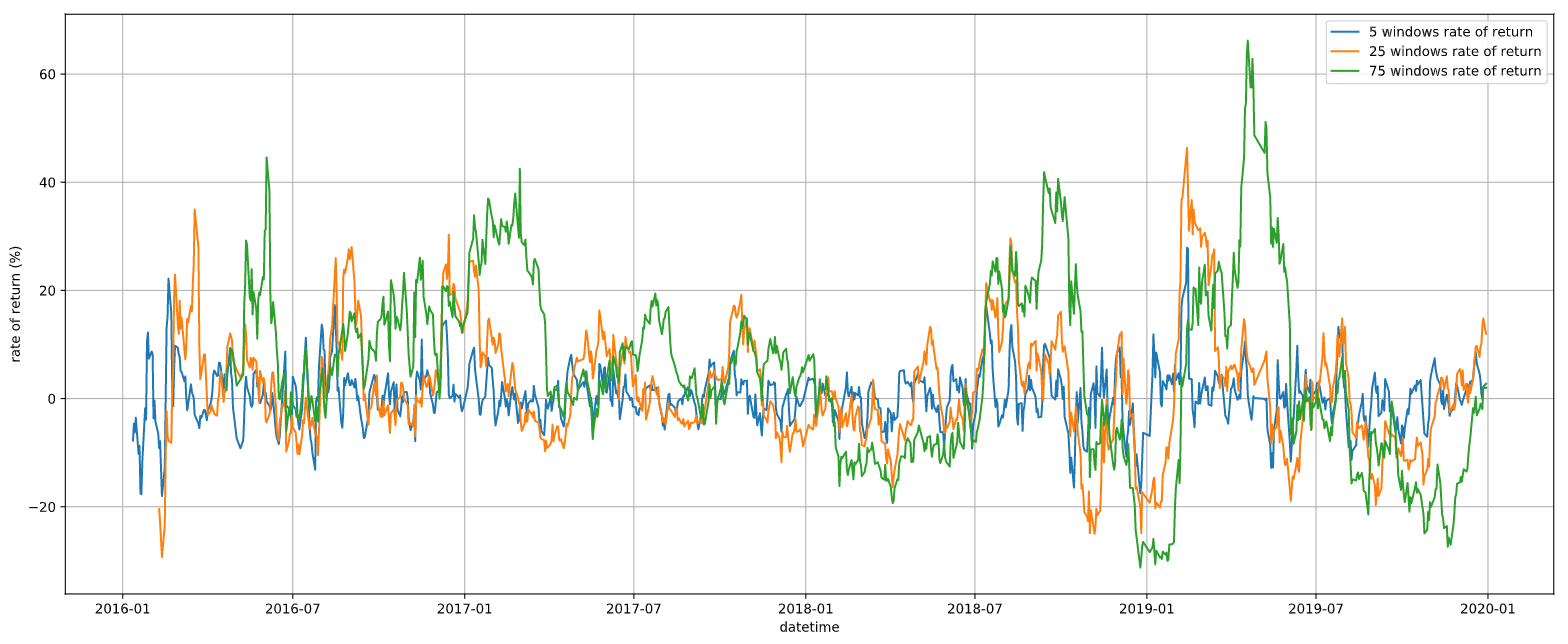
2.5.5. ヒストリカル・ボラティリティ
ここではヒストリカル・ボラティリティを計算します。ここで計算するヒストリカル・ボラティリティは、5日、25日、75日の対数リターンの標準偏差です。ヒストリカル・ボラティリティはリスク指標の一つで、価格がどの程度激しく変動したかを把握するために利用します。一般的にヒストリカル・ボラティリティが大きい銘柄は、小さい銘柄よりも資産として保持するリスクが相対的に高いと考えられます。
# stock_priceの読み込み
price = dfs["stock_price"]
# 特定の銘柄コードに絞り込み
code = 9984
price_data = price[price["Local Code"] == code]
# 2019年までの値を表示
price_data = price_data[:"2019"].copy()
# 5日、25日、75日のヒストリカル・ボラティリティを算出
periods = [5, 25, 75]
cols = []
for period in periods:
col = "{} windows volatility".format(period)
price_data[col] = np.log(price_data["EndOfDayQuote ExchangeOfficialClose"]).diff().rolling(period).std()
cols.append(col)
# プロット
fig, ax = plt.subplots(figsize=(20, 8))
for col in cols:
ax.plot(price_data[col], label=col)
ax.set_ylabel("volatility")
ax.set_xlabel("datetime")
ax.grid(True)
ax.legend()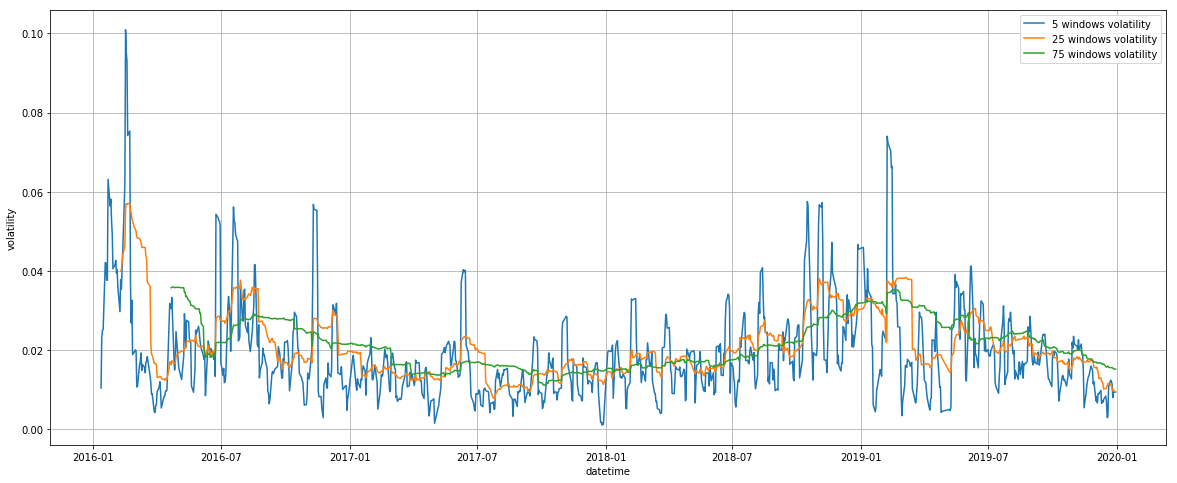
2.5.6. 複数の株価データを同時にプロット
これまで可視化してきた株価に関するデータを同時にプロットすることで、それぞれの値の関連性について考察します。
# stock_priceの読み込み
price = dfs["stock_price"]
# 特定の銘柄コードに絞り込み
code = 9984
price_data = price[price["Local Code"] == code]
# 2019年までの値を表示
price_data = price_data[:"2019"].copy()
# 5日、25日、75日を対象に値を算出
periods = [5, 25, 75]
ma_cols = []
# 移動平均線
for period in periods:
col = "{} windows simple moving average".format(period)
price_data[col] = price_data["EndOfDayQuote ExchangeOfficialClose"].rolling(period, min_periods=1).mean()
ma_cols.append(col)
return_cols = []
# 価格変化率
for period in periods:
col = "{} windows rate of return".format(period)
price_data[col] = price_data["EndOfDayQuote ExchangeOfficialClose"].pct_change(period) * 100
return_cols.append(col)
vol_cols = []
# ヒストリカル・ボラティリティ
for period in periods:
col = "{} windows volatility".format(period)
price_data[col] = np.log(price_data["EndOfDayQuote ExchangeOfficialClose"]).diff().rolling(period).std()
vol_cols.append(col)
# プロット
fig, ax = plt.subplots(nrows=3 ,figsize=(20, 8))
ax[0].plot(price_data["EndOfDayQuote ExchangeOfficialClose"], label="Close Price")
for col in ma_cols:
ax[0].plot(price_data[col], label=col)
for col in return_cols:
ax[1].plot(price_data[col], label=col)
for col in vol_cols:
ax[2].plot(price_data[col], label=col)
ax[0].set_ylabel("stock_price")
ax[1].set_ylabel("rate of return (%)")
ax[2].set_ylabel("volatility (log return)")
for _ax in ax:
_ax.set_xlabel("datetime")
_ax.grid(True)
_ax.legend()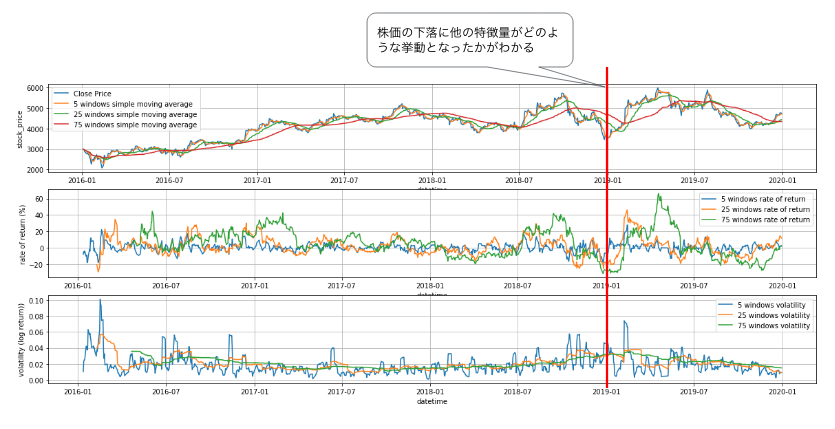
ここでは2018年末に起きた株価の下落に着目してみます。複数の特徴量を並べてプロットすると、株価に大きな変動があった時に他の特徴量にどのような影響を与えているかを観測することができます。
移動平均の特徴量は、期間が短いほど敏感に株価の下落に反応し、期間が長い特徴量ほど反応が遅れることがわかります。リターンの特徴量も下落時には同一の傾向が見て取れますが、その後高いリターンが観測されることがわかります。一方、ヒストリカル・ボラティリティの挙動をみると、下落の前にじわじわとボラティリティが上昇していることがわかります。このように一つの株価の下落を見ても、それぞれの特徴量の挙動が微妙に異なっており、複数個の特徴量をモデルに投入することで、これらの挙動のパターンを学習することが想像できます。
2.6. データセットの前処理
ここまでデータの読み込み及び可視化について説明してきましたが、ここからはデータの前処理やモデル構築に関して説明していきます。 大まかな流れは、次の図のとおりです。
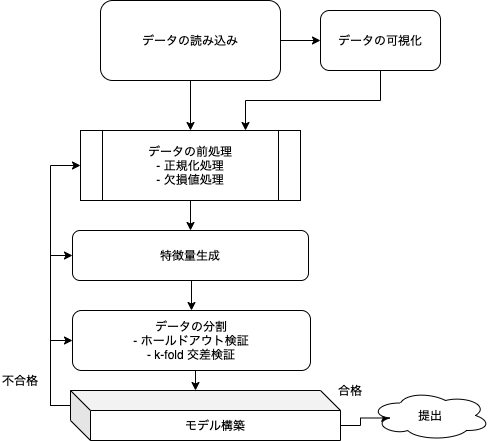
上図のとおり、モデルを構築する際には、データセットをそのまま入力するのではなく、欠損値処理や正規化処理などのデータセットの前処理を実施してから入力することが一般的です。ここではデータセットの前処理について解説していきます。
2.6.1. 欠損値処理
機械学習モデルの多くは欠損値をそのまま扱うことができないため、補完するなどして対処する必要があります。欠損値補完の方法としては、平均値埋めやリストワイズ法、多重代入法などが存在します。また、変数に欠損が存在するレコードを単に除外することや、欠損を多く含む変数自体を除外することも考えられます。
2.6.2. 欠損値の処理方法
本コンペティションのデータについて、まずは実際に欠損が発生している箇所やパターンを特定するために、欠損の発生状況をプロットして確認してみます。
# stock_finデータを読み込む
stock_fin = dfs["stock_fin"]
# 2019年までの値を表示
stock_fin = stock_fin[:"2019"]
# データ数の確認
print(stock_fin.shape)
# データの欠損値数を確認
print(stock_fin.isna().sum())
# 欠損値の数を年別に集計
stock_fin = stock_fin.isna()
stock_fin["year"] = stock_fin.index.year
# データの欠損値をプロット
fig, ax = plt.subplots(figsize=(20, 5))
sns.heatmap(stock_fin.groupby("year").agg("sum"), ax=ax)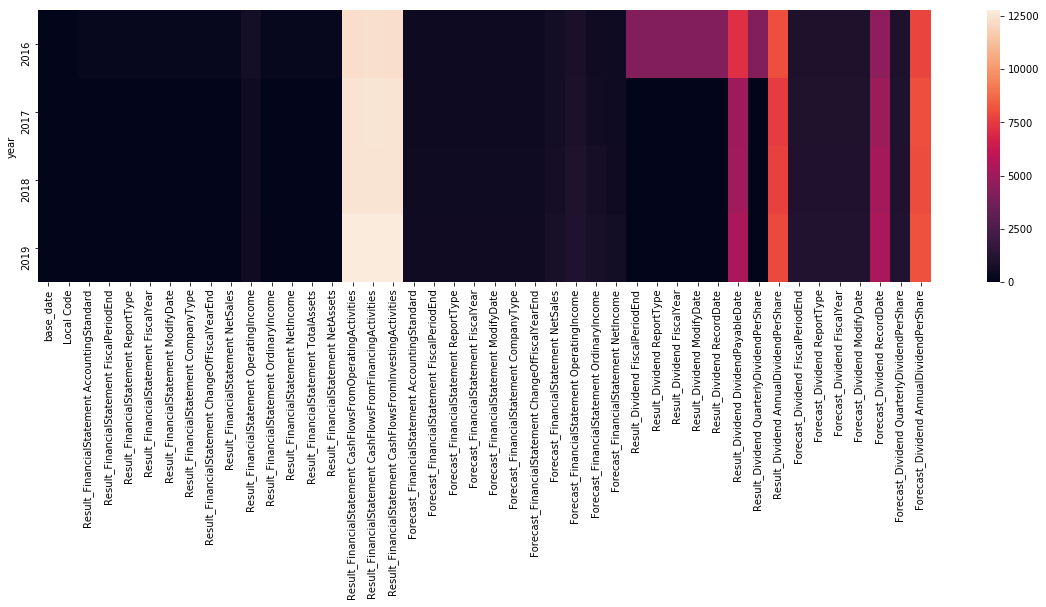
明るい色で示されている箇所は、欠損値が多く発生していることを表しています。本チュートリアルでは欠損値について以下のように対応します。
・`Result_FinancialStatement` の CashFlowsFromOperatingActivities 、 CashFlowsFromFinancingActivities 、 CashFlowsFromInvestingActivities に多くの欠損値があります(上図中央左)。これらのカラムの値は Result_FinancialStatement ReportType が Annual の場合にのみ値が入っています。これらの欠損値については 0 を代入することで対処します。
・配当支払開始日を表す Result_Dividend DividendPayableDate や予想配当基準日を表す Forecast_Dividend RecordDate というデータ列等のfloat64型以外のデータ列に数多く欠損が発生していることが分かります(上図右側)。そのため、本チュートリアルではfloat64型として読み込まれているカラムのみを使用することとします。
・上記に記載したキャッシュフローに関するカラム以外のfloat64型として読み込まれているカラムの欠損値についても、 0 を代入することで対処します。ただし、変数によっては、0という数字自体に意味があるケースが有るため、気をつける必要があります。
実際の欠損値処理は、次のように変数の型 (今回は np.float64 という型を選択) 別に後段処理できる値 (今回は 0) で欠損値を埋めます。
# stock_finデータを読み込む
stock_fin = dfs["stock_fin"]
# 銘柄コード9984にデータを絞る
code = 9984
stock_fin = stock_fin[stock_fin["Local Code"] == code]
# float64型の列に絞り込み
fin_data = stock_fin.select_dtypes(include=["float64"])
# 欠損値を0でフィル
fin_data = fin_data.fillna(0)2.7. 特徴量の生成
2.7.1. なぜ特徴量の設計が重要なのか
機械学習の手法にはモデルにできるだけ生に近いデータを与えてその関係性を見つける手法とドメイン知識や専門性を活かして、特徴量を設計する手法があります。
前者の手法はEnd-To-End Learningと呼ばれ、生に近いデータをモデルに与え、そのモデル自体に特徴量を発見させる手法です。音声認識などの分野で活用されています。
本チュートリアルでは、金融データに慣れ親しんでいただくためにも、特徴量の影響を細かく考察しながら汎化性能に貢献する特徴量を設計していくアプローチで、モデルを構築します。
特徴量生成は、仮説を考え、その仮説をモデルが学ぶにはどのような特徴量が必要か、ということを想像することが重要です。
本チュートリアルでは、「直近株価が上がったら、高値もより大きく変動しやすい」という仮説を立て、この仮説を基に特徴量を生成してみます。この仮説をモデルが学ぶためには直近株価が上がったことを示す特徴量が必要です。直近を仮に1ヶ月と仮定すると、20日リターンや20日移動平均乖離率などが候補になります。
また、この仮説が市場においても必ずしも正しいという必要はなく、仮説を思いついたら、その仮説を学ぶことができる特徴量を想像し、実際に実験してみることが重要です。
2.7.2. 定常性を意識した特徴量設計
時系列データを扱う際には、定常性を意識して特徴量を設計することが重要です。
株価をそのまま学習させたケースと定常性がある特徴量を利用するケースについて考えてみます。
株価をそのまま学習させたケース: 例えば、モデルの訓練期間における株価が、100円〜110円の範囲で動いたとします。もし、この数値をそのままモデルに投入すると、モデルは株価が100円〜110円近辺で動くことを暗黙に学習します。しかし、この暗黙の仮定は実際のマーケットでは成立しておらず、テスト期間で株価が高騰すると、モデルがうまく動かないことがあります。他にも株価に特有の例としては株式分割や株式併合により株価のレンジが大きく変動する場合があります。
定常性がある特徴量を利用するケース: 例えば、20日の価格変化率を考えると、これは正規分布ではありませんが、一部のマーケットの混乱期を除けばほぼ0を中心とした正規分布に近い分布になります。特徴量は、2%の上昇や4%の下落といった0を中心とした時系列となっており、将来に渡っても似たような分布になることが期待でき、株価範囲に対する暗黙の仮定を学ぶ恐れがなくなります。このように将来に渡っても似たような分布を期待できる特徴量は定常性があるといえます。
定常性を意識すると、正規化処理における様々な注意点が見えてきます。たとえば、最小値と最大値を-1から1などにマッピングするMinMax正規化を株価に適用したとしても定常性を期待することはできません。株価をMinMax正規化したときにその最大値・最小値が未来に対しても適用できる保証ができないためです。このように時系列の特徴量の設計をするとき、定常性を意識しながら特徴量を設計していくことが重要です。
2.7.3. 特徴量の生成例
ここでは、特徴量の生成を stock_price の株価情報を利用して行います。株価情報には、価格や出来高など市場で公開されている株価の四本値(始値、高値、安値、終値)の時系列データが格納されています。本チュートリアルでは、特徴量の例として1ヶ月、2ヶ月、3ヶ月間の「終値の変化率(リターン)」、「ヒストリカル・ボラティリティ」、「移動平均線からの乖離率」を紹介します。
次のコードで具体的な計算については示しますが、定義は以下のとおりです。
| 特徴量の計算に使用する関数 | 使用する関数の説明 |
|---|---|
pct_change(N) |
現在の観測値とN個前の観測値との変化率 |
diff() |
現在の観測値と一つ前の観測値との差 |
rolling(N) |
対象の観測値をN個でグループ化 |
std() |
標準偏差 |
mean() |
算術平均 |
# stock_priceデータを読み込む
price = dfs["stock_price"]
# 銘柄コード9984にデータを絞る
code = 9984
price_data = price[price["Local Code"] == code]
# 終値のみに絞る
feats = price_data[["EndOfDayQuote ExchangeOfficialClose"]].copy()
# 終値の20営業日リターン
feats["return_1month"] = feats["EndOfDayQuote ExchangeOfficialClose"].pct_change(20)
# 終値の40営業日リターン
feats["return_2month"] = feats["EndOfDayQuote ExchangeOfficialClose"].pct_change(40)
# 終値の60営業日リターン
feats["return_3month"] = feats["EndOfDayQuote ExchangeOfficialClose"].pct_change(60)
# 終値の20営業日ボラティリティ
feats["volatility_1month"] = (
np.log(feats["EndOfDayQuote ExchangeOfficialClose"]).diff().rolling(20).std()
)
# 終値の40営業日ボラティリティ
feats["volatility_2month"] = (
np.log(feats["EndOfDayQuote ExchangeOfficialClose"]).diff().rolling(40).std()
)
# 終値の60営業日ボラティリティ
feats["volatility_3month"] = (
np.log(feats["EndOfDayQuote ExchangeOfficialClose"]).diff().rolling(60).std()
)
# 終値と20営業日の単純移動平均線の乖離
feats["MA_gap_1month"] = feats["EndOfDayQuote ExchangeOfficialClose"] / (
feats["EndOfDayQuote ExchangeOfficialClose"].rolling(20).mean()
)
# 終値と40営業日の単純移動平均線の乖離
feats["MA_gap_2month"] = feats["EndOfDayQuote ExchangeOfficialClose"] / (
feats["EndOfDayQuote ExchangeOfficialClose"].rolling(40).mean()
)
# 終値と60営業日の単純移動平均線の乖離
feats["MA_gap_3month"] = feats["EndOfDayQuote ExchangeOfficialClose"] / (
feats["EndOfDayQuote ExchangeOfficialClose"].rolling(60).mean()
)
# 欠損値処理
feats = feats.fillna(0)
# 元データのカラムを削除
feats = feats.drop(["EndOfDayQuote ExchangeOfficialClose"], axis=1)2.7.4. テクニカル分析を活用した特徴量の生成
他に株価を扱うための特徴量としてRSIやストキャスティクスのようなテクニカル分析の指標などを活用することもあります。テクニカル分析の利用に関する考察は本章では取り扱わずに、第7章で紹介しています。
2.8. バックテスト用のテストデータ作成
ここでは、バックテストを行うためのデータの分割について説明します。
2.8.1. バックテストとは
バックテストとは、モデルの有効性を検証する際に、過去のデータを用いて、一定期間にどの程度のパフォーマンスが得られたかをシミュレーションすることです。モデルの有効性を検証する上で、どのようにバックテストを実施するかは重要なポイントになります。
2.8.2. ホールドアウト検証
ここでは、データセットを訓練データとテストデータに切り分けます。まずデータセットを分ける理由を説明し、次に、データセットの分け方及びコツについて解説します。
データセットを分ける理由は、モデルの汎化性能を確認し使用するモデルを決定するためです。
汎化性能とは、モデルが訓練データ以外の未知のデータに対しても機能するという能力です。汎化性能が低いモデルは、訓練データでは高い精度が得られますが、訓練データにない未知のデータについては、低い精度しか得られません。この現象を過学習と呼びます。データセットを分割せずに、そのまま全体に対して学習し、同じデータセットに対してモデルによる予測をすると、基本的には高い精度の結果を得ることができます。
しかし、未知のデータに対して予測すると、予測がまったく当たらないということが起こり得ます。そのため、データセットを分割して、学習に使用していないデータをモデルの検証用として用意しておくことで、作成したモデルが過学習していないことを確認することが出来ます。
基本的な時系列データの分割手法(ホールドアウト検証)に関して解説します。
1.全体のデータセットを、訓練期間(TRAIN)/検証期間(VAL)/テスト期間(TEST)で分けます。 2.TRAINデータでモデルを学習させ、VALデータでモデルを評価します。これをモデルのさまざまなパラメーターで何度か行い、一番結果が良かったパラメーターを選びます。 3.そして最後にTESTデータでモデルの予測結果を最終評価します。
本チュートリアルでは、次の期間でデータを分割します。
訓練期間 |
2016-01-01 - 2017-12-31 |
|---|---|
評価期間 |
2018-02-01 - 2018-12-01 |
テスト期間 |
2019-01-01 - 2020-12-31 |
※データの分割に際し、各期間に間隔(1か月)を空けている理由は、未来の情報を含ませないようにするためです。例えば、2017年12月31日の目的変数には5営業日、10営業日、20営業日後の株価リターンの情報が入っているため、2017年12月31日のデータを使って学習したモデルは未来の情報(2018年1月のリターン)を知っていることになってしまいます。したがって、2018年1月のデータを検証データに含めてしまうとリークが発生し、適切なモデルの評価ができなくなってしまいます。
以下のように変数を定義しておきます。
TRAIN_END = "2017-12-31"
VAL_START = "2018-02-01"
VAL_END = "2018-12-01"
TEST_START = "2019-01-01"2.8.3. その他の検証方法
・k-fold 交差検証(k-fold CV): データをまず訓練データとテストデータに分け、その後その訓練データをk個のグループに分割し、k-1個のグループに含まれるものを訓練データ、残りの1個のグループに含まれるものを評価データとすると、このような分割方法はk通り考えられます。
そこで、それぞれの分割方法したがってk回訓練と評価を行い、それぞれの試行結果の平均などを使用して、モデルやそのモデルのパラメータを評価します。なお、時系列データでは、将来の情報を含まないように注意する必要があります。
2.9. モデルの構築
ここでは、モデルの学習に用いるためのデータを準備します。
モデル作成のステップは、以下のとおりに行います。
1. 銘柄を一つ選ぶ 2. その銘柄に対して、財務データ及びマーケットデータから特徴量を作る 3. 全銘柄に対して同じことを繰り返す 4. 作成したデータを結合する 5. 全データを訓練データ、評価データ、テストデータに分ける 6. 訓練データで予測モデルを学習させる
・入力用データの作成方法
前回までのマーケットデータを用いた特徴量生成方法、及び財務諸表データの欠損値処理を行った後のデータ処理について解説し、今回はそれらのデータを結合させ、モデルが学習できるフォーマットに直すことが目的です。
2.9.1. 特徴量の生成
ここでは、特徴量生成のコードを示しています。コードのおおまかな流れとしては、以下の3ステップに分けられます。
1. 財務データの取得及び前処理(Chapter 2.6.2と同様) 2. マーケットデータの取得及び特徴量定義(Chapter 2.7.2と同様) 3. 財務データと生成した特徴量を結合
def get_features_for_predict(dfs, code, start_dt="2016-01-01"):
"""
Args:
dfs (dict) : dict of pd.DataFrame include stock_fin, stock_price
code (int) : A local code for a listed company
start_dt (str): specify date range
Returns:
feature DataFrame (pd.DataFrame)
"""
# おおまかな手順の1つ目
# stock_finデータを読み込み
stock_fin = dfs["stock_fin"]
# 特定の銘柄コードのデータに絞る
fin_data = stock_fin[stock_fin["Local Code"] == code]
# 特徴量の作成には過去60営業日のデータを使用しているため、
# 予測対象日からバッファ含めて土日を除く過去90日遡った時点から特徴量を生成します
n = 90
# 特徴量の生成対象期間を指定
fin_data = fin_data.loc[pd.Timestamp(start_dt) - pd.offsets.BDay(n) :]
# fin_dataのnp.float64のデータのみを取得
fin_data = fin_data.select_dtypes(include=["float64"])
# 欠損値処理
fin_feats = fin_data.fillna(0)
# おおまかな手順の2つ目
# stock_priceデータを読み込む
price = dfs["stock_price"]
# 特定の銘柄コードのデータに絞る
price_data = price[price["Local Code"] == code]
# 終値のみに絞る
feats = price_data[["EndOfDayQuote ExchangeOfficialClose"]]
# 特徴量の生成対象期間を指定
feats = feats.loc[pd.Timestamp(start_dt) - pd.offsets.BDay(n) :].copy()
# 終値の20営業日リターン
feats["return_1month"] = feats["EndOfDayQuote ExchangeOfficialClose"].pct_change(20)
# 終値の40営業日リターン
feats["return_2month"] = feats["EndOfDayQuote ExchangeOfficialClose"].pct_change(40)
# 終値の60営業日リターン
feats["return_3month"] = feats["EndOfDayQuote ExchangeOfficialClose"].pct_change(60)
# 終値の20営業日ボラティリティ
feats["volatility_1month"] = (
np.log(feats["EndOfDayQuote ExchangeOfficialClose"]).diff().rolling(20).std()
)
# 終値の40営業日ボラティリティ
feats["volatility_2month"] = (
np.log(feats["EndOfDayQuote ExchangeOfficialClose"]).diff().rolling(40).std()
)
# 終値の60営業日ボラティリティ
feats["volatility_3month"] = (
np.log(feats["EndOfDayQuote ExchangeOfficialClose"]).diff().rolling(60).std()
)
# 終値と20営業日の単純移動平均線の乖離
feats["MA_gap_1month"] = feats["EndOfDayQuote ExchangeOfficialClose"] / (
feats["EndOfDayQuote ExchangeOfficialClose"].rolling(20).mean()
)
# 終値と40営業日の単純移動平均線の乖離
feats["MA_gap_2month"] = feats["EndOfDayQuote ExchangeOfficialClose"] / (
feats["EndOfDayQuote ExchangeOfficialClose"].rolling(40).mean()
)
# 終値と60営業日の単純移動平均線の乖離
feats["MA_gap_3month"] = feats["EndOfDayQuote ExchangeOfficialClose"] / (
feats["EndOfDayQuote ExchangeOfficialClose"].rolling(60).mean()
)
# おおまかな手順の3つ目
# 欠損値処理
feats = feats.fillna(0)
# 元データのカラムを削除
feats = feats.drop(["EndOfDayQuote ExchangeOfficialClose"], axis=1)
# 財務データの特徴量とマーケットデータの特徴量のインデックスを合わせる
feats = feats.loc[feats.index.isin(fin_feats.index)]
fin_feats = fin_feats.loc[fin_feats.index.isin(feats.index)]
# データを結合
feats = pd.concat([feats, fin_feats], axis=1).dropna()
# 欠損値処理を行います。
feats = feats.replace([np.inf, -np.inf], 0)
# 銘柄コードを設定
feats["code"] = code
# 生成対象日以降の特徴量に絞る
feats = feats.loc[pd.Timestamp(start_dt) :]
return featsここで、 np.inf を0に置換していますが、価格変化率の計算の際に発散してしまったものを、0と定義し直しています。このように、特徴量を定義する際に、特徴量変換により発散してしまった時やnanになった時の処理を、あらかじめ考慮しておくことがスムーズにデータセットを構築する上で重要です。
次にここまでの処理の結果を確認します。
df = get_features_for_predict(dfs, 9984)
df.T2.9.2. 目的変数の対応付け及び訓練データ、評価データ、テストデータの分割
次に目的変数を定義します。目的変数は、データセットの stock_labels 内にあり、利用する際は先ほど定義した特徴量のデータセットに対して、行(日付)を一致させる必要があります。
データセットの訓練期間、評価期間、テスト期間への分割処理も合わせて実施します。
def get_features_and_label(dfs, codes, feature, label):
"""
Args:
dfs (dict[pd.DataFrame]): loaded data
codes (array) : target codes
feature (pd.DataFrame): features
label (str) : label column name
Returns:
train_X (pd.DataFrame): training data
train_y (pd.DataFrame): label for train_X
val_X (pd.DataFrame): validation data
val_y (pd.DataFrame): label for val_X
test_X (pd.DataFrame): test data
test_y (pd.DataFrame): label for test_X
"""
# 分割データ用の変数を定義
trains_X, vals_X, tests_X = [], [], []
trains_y, vals_y, tests_y = [], [], []
# 銘柄コード毎に特徴量を作成
for code in tqdm(codes):
# 特徴量取得
feats = feature[feature["code"] == code]
# stock_labelデータを読み込み
stock_labels = dfs["stock_labels"]
# 特定の銘柄コードのデータに絞る
stock_labels = stock_labels[stock_labels["Local Code"] == code]
# 特定の目的変数に絞る
labels = stock_labels[label]
# nanを削除
labels.dropna(inplace=True)
if feats.shape[0] > 0 and labels.shape[0] > 0:
# 特徴量と目的変数のインデックスを合わせる
labels = labels.loc[labels.index.isin(feats.index)]
feats = feats.loc[feats.index.isin(labels.index)]
labels.index = feats.index
# データを分割(ホールドアウト法)
_train_X = feats[: TRAIN_END]
_val_X = feats[VAL_START : VAL_END]
_test_X = feats[TEST_START :]
_train_y = labels[: TRAIN_END]
_val_y = labels[VAL_START : VAL_END]
_test_y = labels[TEST_START :]
# データを配列に格納 (後ほど結合するため)
trains_X.append(_train_X)
vals_X.append(_val_X)
tests_X.append(_test_X)
trains_y.append(_train_y)
vals_y.append(_val_y)
tests_y.append(_test_y)
# 銘柄毎に作成した説明変数データを結合します。
train_X = pd.concat(trains_X)
val_X = pd.concat(vals_X)
test_X = pd.concat(tests_X)
# 銘柄毎に作成した目的変数データを結合します。
train_y = pd.concat(trains_y)
val_y = pd.concat(vals_y)
test_y = pd.concat(tests_y)
return train_X, train_y, val_X, val_y, test_X, test_y次に、ここまでの結果を確認します。
# 対象銘柄コードを定義
codes = [9984]
# 対象の目的変数を定義
label = "label_high_20"
# 特徴量を取得
feat = get_features_for_predict(dfs, codes[0])
# 特徴量と目的変数を入力し、分割データを取得
ret = get_features_and_label(dfs, codes, feat, label)
for v in ret:
print(v.T)ここまでは一つの銘柄に対して処理をしてきましたが、ここからは全ての予測対象銘柄に対して上記の処理を実施するために、予測対象の銘柄コードを以下のように取得します。
def get_codes(dfs):
"""
Args:
dfs (dict[pd.DataFrame]): loaded data
Returns:
array: list of stock codes
"""
stock_list = dfs["stock_list"].copy()
# 予測対象の銘柄コードを取得
codes = stock_list[stock_list["prediction_target"] == True][
"Local Code"
].values
return codes次に、目的変数毎にデータセットを作成します。今回は全ての目的変数に同一の特徴量を使用していますが、目的変数に応じて特徴量をチューニングすることでより精度の高いモデルを作成することができます。
# 対象の目的変数を定義
labels = {
"label_high_5",
"label_high_10",
"label_high_20",
"label_low_5",
"label_low_10",
"label_low_20",
}
# 目的変数毎にデータを保存するための変数
train_X, val_X, test_X = {}, {}, {}
train_y, val_y, test_y = {}, {}, {}
# 予測対象銘柄を取得
codes = get_codes(dfs)
# 特徴量を作成
buff = []
for code in tqdm(codes):
feat = get_features_for_predict(dfs, code)
buff.append(feat)
feature = pd.concat(buff)
# 目的変数毎に処理
for label in tqdm(labels):
# 特徴量と目的変数を取得
_train_X, _train_y, _val_X, _val_y, _test_X, _test_y = get_features_and_label(dfs, codes, feature, label)
# 目的変数をキーとして値を保存
train_X[label] = _train_X
val_X[label] = _val_X
test_X[label] = _test_X
train_y[label] = _train_y
val_y[label] = _val_y
test_y[label] = _test_y2.9.3. モデル学習の実行方法
データの準備が完了したので、いよいよモデルの学習を実行します。ここでは、sklearnライブラリのRandomForestRegressorモデルを使用します。モデルに設定する各種パラメータは、ここではとくに指定せずにライブラリのデフォルトパラメータを使用します。
RandomForestの回帰モデルであるRandomForestRegressorモデルを利用する理由は、予測する目的変数が連続値であるからです。RandomForestモデルは決定木をベースとするモデルであるため、以下の理由から最初に選択するモデルとして扱いやすいです。
-
RandomForest内部で利用する決定木は、特徴量の大小関係のみに着目しており、値自体には意味がないので正規化処理の必要がありません
-
特徴量の重要度を取得することができ、次に実施することの道筋を立てやすい
# 目的変数を指定
label = "label_high_20"
# モデルの初期化
pred_model = RandomForestRegressor(random_state=0)
# モデルの学習
pred_model.fit(train_X[label], train_y[label])一方、サポートベクターマシンやニューラルネットワークを利用する際は、データの前処理における注意点が増えます。選択するモデルの特性に応じた正規化処理と特徴量設計が重要です。
2.10. モデルの推論
ここでは構築したモデルから予測結果を出力し、可視化などによる分析を実施します。
2.10.1. 予測結果の出力方法
ここまで、それぞれの目的変数に対して、訓練データ、評価データ、テストデータに分割しました。ここからは、モデルの学習完了後に、テストデータを入力として予測を出力し、pandas.DataFrame形式に変換します。
# モデルを定義
models = {
"rf": RandomForestRegressor,
}
# モデルを選択
model = "rf"
# 目的変数を指定
label = "label_high_20"
# 学習用データセット定義
# ファンダメンタル情報
fundamental_cols = dfs["stock_fin"].select_dtypes("float64").columns
fundamental_cols = fundamental_cols[fundamental_cols != "Result_Dividend DividendPayableDate"]
fundamental_cols = fundamental_cols[fundamental_cols != "Local Code"]
# 価格変化率
returns_cols = [x for x in train_X[label].columns if "return" in x]
# テクニカル
technical_cols = [x for x in train_X[label].columns if (x not in fundamental_cols) and (x != "code")]
columns = {
"fundamental_only": fundamental_cols,
"return_only": returns_cols,
"technical_only": technical_cols,
"fundamental+technical": list(fundamental_cols) + list(technical_cols),
}
# 学習用データセットを指定
col = "fundamental_only"
# 学習
pred_model = models[model](random_state=0)
pred_model.fit(train_X[label][columns[col]].values, train_y[label])
# 予測
result = {}
result[label] = pd.DataFrame(
pred_model.predict(val_X[label][columns[col]]), columns=["predict"]
)
# 予測結果に日付と銘柄コードを追加
result[label]["datetime"] = val_X[label][columns[col]].index
result[label]["code"] = val_X[label]["code"].values
# 予測の符号を取得
result[label]["predict_dir"] = np.sign(result[label]["predict"])
# 実際の値を追加
result[label]["actual"] = val_y[label].values2.10.2. 予測結果の可視化方法
予測結果の確認として、実際に決算開示等のあった銘柄について基準日付の終値から最高値への変化率(actual)と予測スコア(predict)の散布図を見ます。ここで散布図を選択する理由は、予測対象に対して予測スコアがどのような分布をとっているかを見ることが、モデルの挙動を理解するわかりやすい可視化であることが挙げられます。
sns.jointplot(data=result[label], x="predict", y="actual")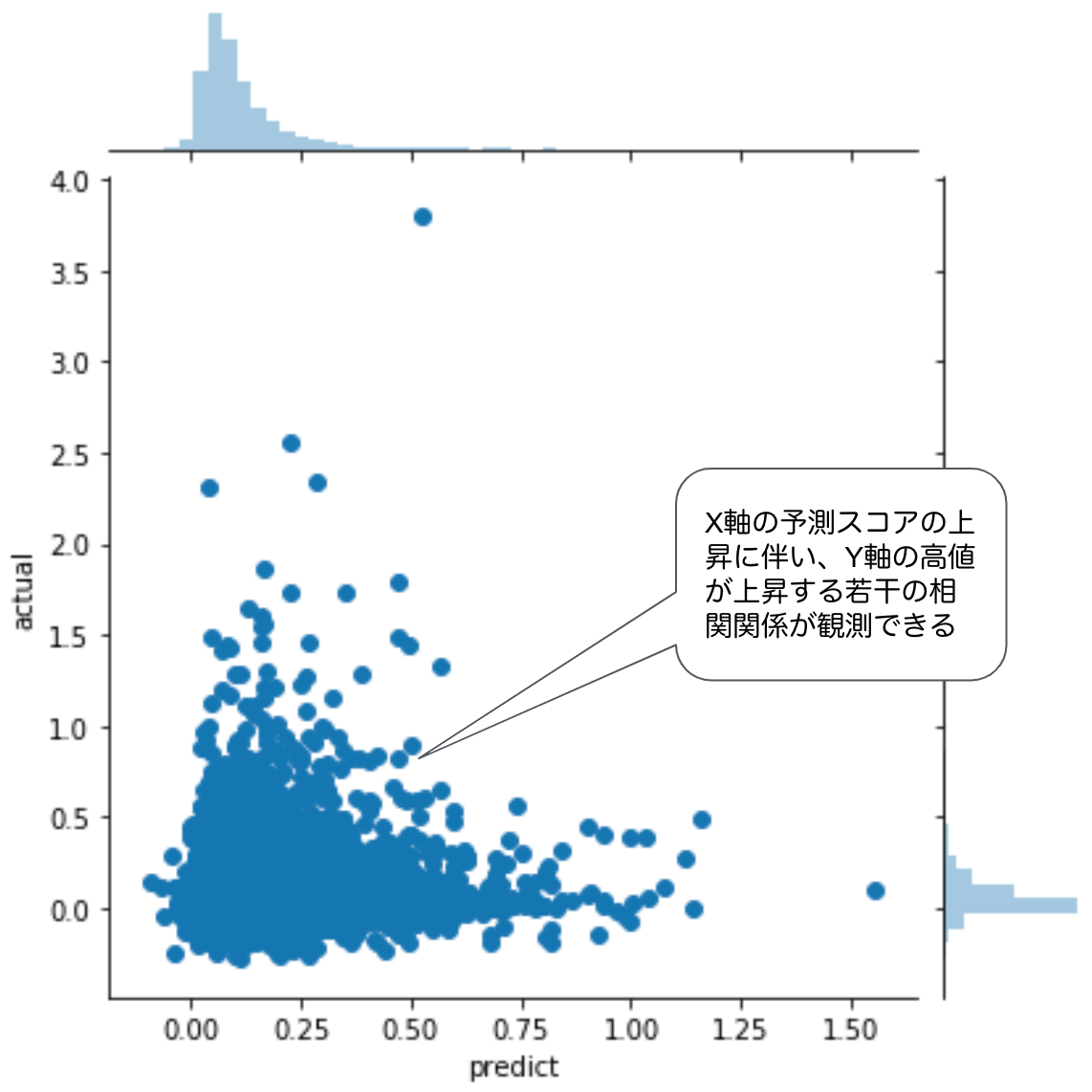
この図では、横軸が予測値で、縦軸が真の値です。予測と真の値には、正の相関(0.144192)が見受けられるので、ある程度の相関関係が発生しています。一般的なデータで0.144という数字が出てもほぼ無相関に見えますが、金融データでは0.144というスコアは高い部類に入ります。このように視覚化すると、予測値と真の値の関係性を可視化できます。
2.11. 予測結果に対する分析の道筋
予測精度を向上させるためには、特徴量とモデルの分析を集中的に行う必要があります。特徴量の分析では、さまざまな手法がありますが、ここでは特徴量の重要度の分析とSHAPという手法を紹介します。
2.11.1. 特徴量の重要度
特徴量の重要度は、Random ForestやGradient Boostingなどのいくつかの機械学習モデルで取得でき、モデル内でどの程度それぞれの説明変数が、目的変数に対して重要であるかを判断するために参考になる指標です。
重要度が極端に低いものは、そもそも説明変数から除外したり、重要度が高いものは更に分析することで、性能の向上が期待できないか、など分析の道筋をつける上でも役に立ちます。
ここではファンダメンタル情報を用いて、モデルの訓練データ(2016年初から2017年末まで)における特徴量の重要度を調査します。
次の方法に従って、特徴量の重要度をプロットします。
# 学習済みモデルを指定
rf = pred_model
# 重要度順を取得
sorted_idx = rf.feature_importances_.argsort()
# プロット
fig, ax = plt.subplots(figsize=(8, 8))
ax.barh(fundamental_cols[sorted_idx], rf.feature_importances_[sorted_idx])
ax.set_xlabel("Random Forest Feature Importance")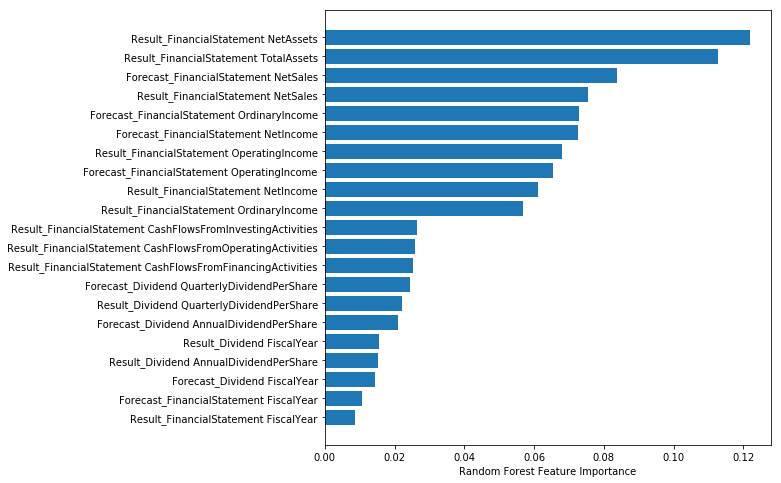
上記の可視化により、 一番上にある NetAssets(純資産) にモデルが注目していることがわかります。純資産は資本金や利益剰余金などを合算した指標で、次に登場する TotalAssets(総資産) から負債を引いたものとなります。 TotalAssets(総資産) は、流動資産や固定資産、繰延資産など、会社の全ての資産を合算したものを示す指標です。
この2つは会社の規模を示す代表的な指標となっています。
Random Forestモデルの内部で、この2つを利用した分岐が多数存在していることを示しており、会社規模が重要な指標である可能性を示唆しています。
2.11.2. SHAP
SHAPは、学習済みモデルにおいて、各特徴量がモデルの出力する予測値に与えた影響度を算出してくれるものです。
ここでは、サンプルモデルとしてXGBoostモデルを利用し、 label_high_20 という目的変数に対して、どの特徴量が学習に効果的な特徴量なのかを見てみます。
# モデルを定義します
sample_model = xgboost.train({"learning_rate": 0.01}, xgboost.DMatrix(train_X["label_high_20"], label=train_y["label_high_20"]), 100)次にshap値を求めます。
shap.initjs()
explainer = shap.TreeExplainer(model=sample_model, feature_perturbation='tree_path_dependent', model_output='margin')
# SHAP値
shap_values = explainer.shap_values(X=train_X["label_high_20"])
# プロット
shap.summary_plot(shap_values, train_X["label_high_20"], plot_type="bar")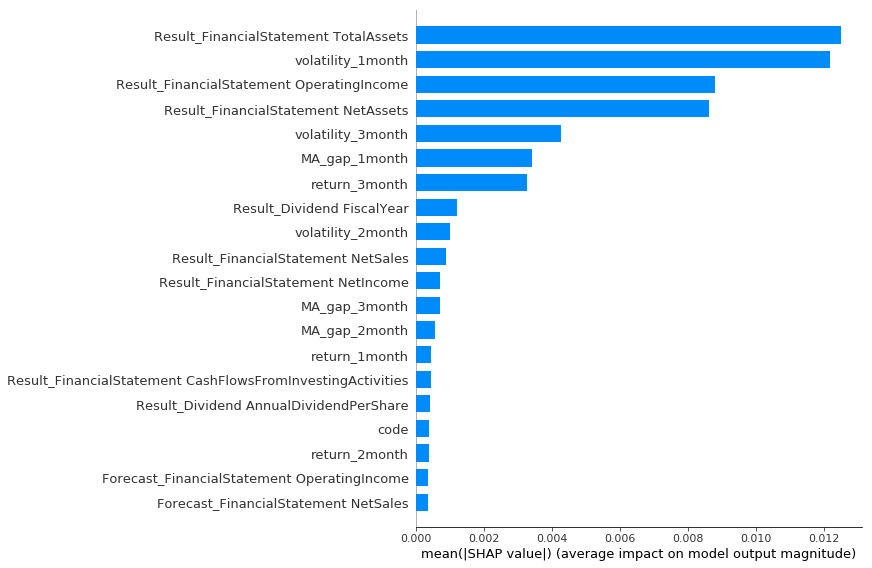
次にshapのsummary_plotを確認します。これは特徴量を少し変化させた時の学習のインパクトを表しています。
shap.summary_plot(shap_values, train_X["label_high_20"])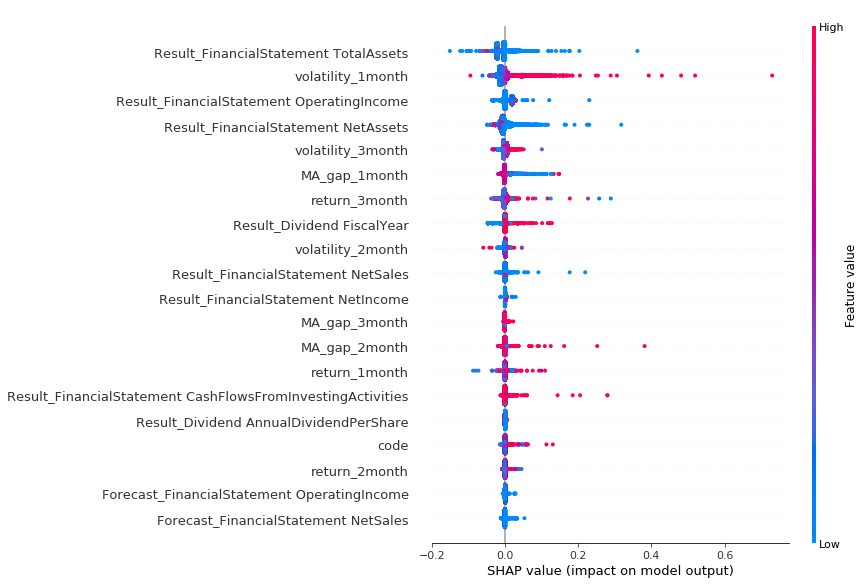
この図の見方ですが、上にある特徴量ほどモデルにとって重要であることを意味します。色が赤いのがその特徴量が高い時、青いのがその特徴量が低い時のSHAP値になります。図からは例えば以下のようなことが読み取れます。
-
Total Assetsが1番目にモデルに影響を与える特徴量であることがわかります。プラス方向、マイナス方向に関わらず青い色が多いので、モデルがTotal Assetsが小さい場合にこの特徴量を活用していることがわかります。Net Assetsも同様の傾向が観測されます -
volatility_1monthがモデルに大きな影響を与える特徴量であることがわかります。この特徴量は赤い時にプラス方向(高値が大きくなる)の影響が大きいことがわかります。これはボラティリティが上昇すると高値が高くなるということを意味するので直感に合致します。 -
MA_gap_1_monthが小さい時にプラス方向(高値が大きくなる)に影響を与えています。移動平均乖離率が小さいときは移動平均線がその時点の株価よりも下にいる期間なので、その時に高値が伸びるのは株価が反転している可能性が高いのかもしれません。
上記のような考察を行いながら、さまざまな特徴量を考え、モデルを改善していくことが重要です。
2.12. モデルの評価
2.12.1. 複数モデルの学習及び結果をまとめる
ここでは、複数モデルを用いて、予測及び結果の比較を行いたいと思います。
今回はシンプルなモデルを複数用います。
| モデル名 | パラメーター |
|---|---|
RandomForestRegressor |
random_state = 0 |
ExtraTreesRegressor |
random_state = 0 |
GradientBoostingRegressor |
random_state = 0 |
次は学習用のデータセットも複数用意します。
| 学習用データセット名 | 説明 |
|---|---|
fundamental_only |
財務諸表データのみ |
return_only |
価格変化率のデータのみ |
technical_only |
テクニカル指標のみ |
fundamental+technical |
財務諸表とテクニカル指標の両方 |
# モデルを定義
models = {
"rf": RandomForestRegressor,
"extraTree": ExtraTreesRegressor,
"gbr": GradientBoostingRegressor,
}
# 学習用データセット定義
columns = {
"fundamental_only": fundamental_cols,
"return_only": returns_cols,
"technical_only": technical_cols,
"fundamental+technical": list(fundamental_cols) + list(technical_cols),
}
# 学習済みモデル保存用
trained_models = dict()
# 結果保存用
all_results = dict()
# モデル毎に処理
for model in tqdm(models.keys()):
all_results[model] = dict()
trained_models[model] = dict()
# データセット毎に処理
for col in tqdm(columns.keys()):
result = dict()
trained_models[model][col] = dict()
# 目的変数毎に処理
for label in tqdm(labels):
if len(test_X[label][columns[col]]) > 0:
# モデル取得
pred_model = models[model](random_state=0)
# 学習
pred_model.fit(train_X[label][columns[col]].values, train_y[label])
# 学習済みモデル保存
trained_models[model][col][label] = pred_model
# 結果データ作成
result[label] = test_X[label][["code"]].copy()
result[label]["datetime"] = test_X[label][columns[col]].index
# 予測
result[label]["predict"] = pred_model.predict(test_X[label][columns[col]])
result[label]["predict_dir"] = np.sign(result[label]["predict"])
# 実際の結果
result[label]["actual"] = test_y[label].values
result[label]["actual_dir"] = np.sign(result[label]["actual"])
result[label].dropna(inplace=True)
all_results[model][col] = result次にデータをまとめます。
results = []
for model in all_results.keys():
for col in all_results[model]:
tmp = pd.concat(all_results[model][col])
tmp["model"] = model
tmp["feature"] = col
results.append(tmp)
results = pd.concat(results)
results["label"] = [x[0] for x in results.index]
results.head(5)
では、次に評価していきます。
2.12.2. モデルの性能を示す評価関数の紹介
まずは、今回用いる評価関数のリストを紹介します。
| 評価関数 | 説明 |
|---|---|
RMSE |
二乗平均平方根 |
accuracy |
目的変数の符号と予測した目的変数の符号の精度 |
spearman_corr |
スピアマンの順位相関 |
corr |
ピアソンの相関係数 |
R^2 score |
単回帰した時の直線と観測値のバラつき |
# 結果保存用変数
all_metrics = []
# データセット毎に処理
for feature in columns:
matrix = dict()
# モデル毎に処理
for model in models:
# 目的変数毎に処理
for label in labels:
# 処理対象データに絞り込み
tmp_df = results[(results["model"] == model) & (results["label"] == label) & (results["feature"] == feature)]
# RMSE
rmse = np.sqrt(mean_squared_error(tmp_df["predict"], tmp_df["actual"]))
# 精度
accuracy = accuracy_score(tmp_df["predict_dir"], tmp_df["actual_dir"])
# 相関係数
corr = np.corrcoef(tmp_df["actual"], tmp_df["predict"])[0, 1]
# 順位相関
spearman_corr = spearmanr(tmp_df["actual"], tmp_df["predict"])[0]
# 結果を保存
matrix[label] = [rmse, accuracy, spearman_corr,corr, corr**2, feature, model, tmp_df.shape[0]]
res = pd.DataFrame.from_dict(matrix).T
res.columns = ["RMSE","accuracy","spearman_corr","corr","R^2 score","feature", "model", "# of samples"]
all_metrics.append(res)
all_metrics = pd.concat(all_metrics)
all_metrics.reset_index()このままだと出力が多すぎるため、集計します。
numeric_cols = ["RMSE","accuracy","spearman_corr","corr","R^2 score"]
for col in numeric_cols:
all_metrics[col] = all_metrics[col].astype(float)
# indexとデータセット毎に平均を計算
agg = all_metrics.reset_index().groupby(["index","feature"]).agg("mean")
agg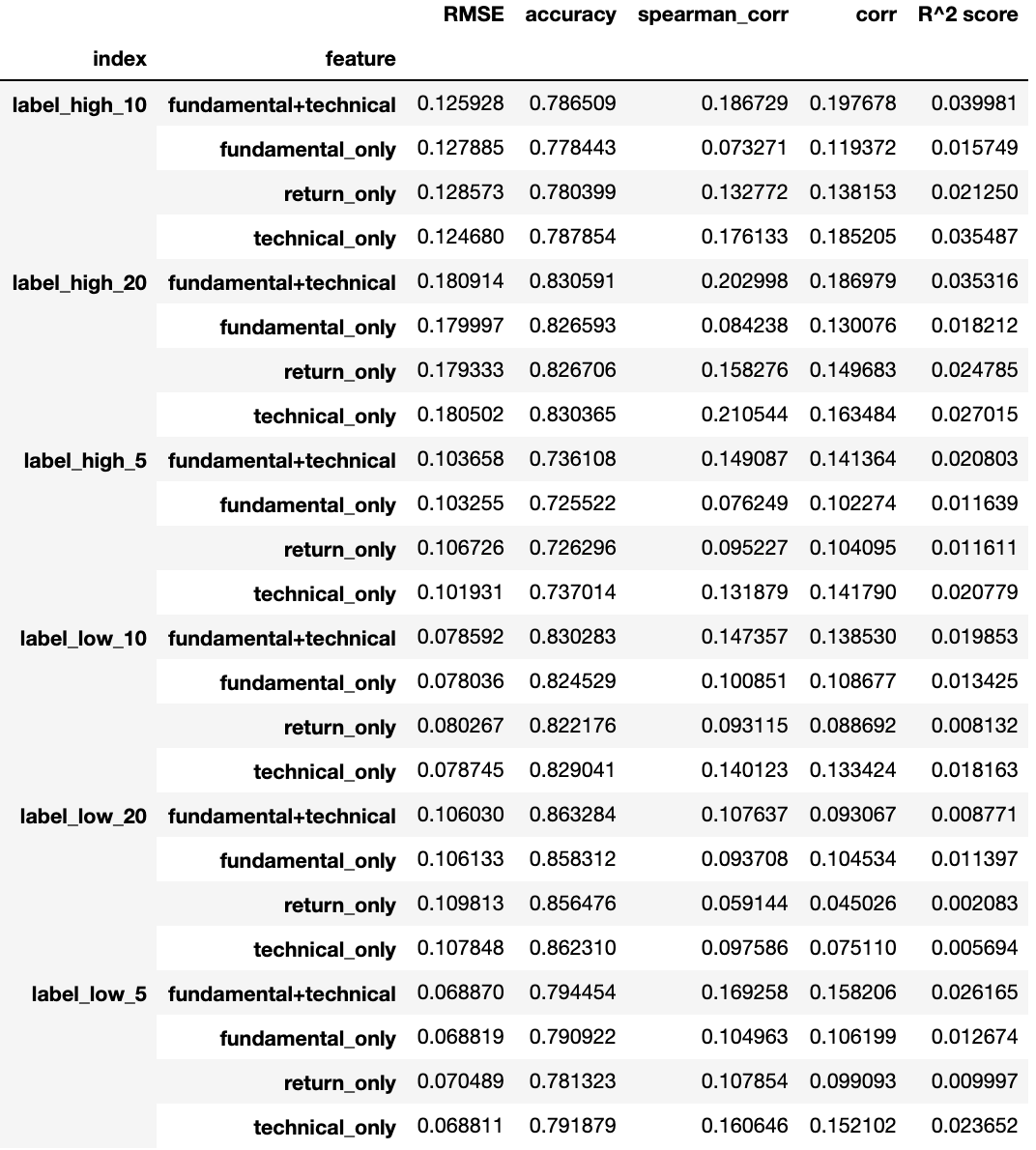
この表のテクニカル分析(technical_only)とファンダメンタルデータ(fundamental_only)にそれぞれ着目すると、テクニカル分析のみを用いた特徴量の方が、ファンダメンタルデータよりも精度(accuracy)という観点で若干優れていることが分かります。
また、テクニカル分析とファンダメンタルデータの両方を特徴量を用いた場合の結果に関しては、テクニカル分析よりも若干全体正解率が高くなっていますが、誤差の範囲内です。相関係数(corr)に関し、テクニカル分析とファンダメンタルデータを両方用いた場合は、用いていない場合に比べて、優れていることが分かります。
このように特徴量を選択しながら複数のモデルをつくり、複数の評価関数で評価を行うことで、テクニカル分析とファンダメンタルデータを組み合わせたアプローチのポテンシャルが高いことがわかります。
2.13. モデルの提出
本コンペティションでは、モデルの予測の提出方法はモデル提出方式になります。以下ではこの方式について簡単に説明しますが、詳しくは SIGNATE: Runtime 投稿方法をご参照ください。
2.13.1. Runtimeの概要
学習済モデルを投稿すると、アルゴリズム (推論プログラム) が実行され、推論時間・推論結果が出力されます。 出力された推論結果は、評価関数(既存の投稿機能)に自動で投稿されます。
SIGNATE: Runtime 投稿方法
2.13.2. 提出ファイルの作成
1.提出ファイルのテンプレートをダウンロード
こちらからダウンロード
2.ディレクトリの構造を確認する
アップロードするディレクトリ構造は次のとおりです。
. ├── model 必須 学習済モデルを置くディレクトリ │ └── ... ├── src 必須 Python のプログラムを置くディレクトリ │ ├── predictor.py 必須 最初のプログラムが呼び出すファイル │ └── ... その他のファイル (ディレクトリ作成可能) └── requirements.txt 任意
3.学習済みモデルの作成
以下の環境でモデルを構築してください。
-
Python3 Anaconda3-2019.03 インストールガイドは次のとおりです。
一般的なケース
https://repo.continuum.io/archive/ からバージョン2019.03をダウンロードしてください
pyenv
pyenv install anaconda3-2019.03
Docker
docker pull continuumio/anaconda3:2019.03
ここで、学習済みモデルの保存方法について説明します。
学習済みモデルは pickle で保存します。保存場所はChapter 2.13.2で説明したディレクトリ構造の学習済みモデルの配置先である model ディレクトリになります。任意のファイル名を設定可能なので、今回はモデルの対象としている目的変数がわかるように my_model_{label}.pkl という名前で保存します。具体的にはモデルの保存は以下のように行います。
# モデル保存用にメソッドを定義します
def save_model(model, label, model_path="../model"):
# モデル保存先ディレクトリを作成
os.makedirs(model_path, exist_ok=True)
with open(os.path.join(model_path, f"my_model_{label}.pkl"), "wb") as f:
# モデルをpickle形式で保存
pickle.dump(model, f)# 保存した学習済みモデルから、提出するモデルを選択してpickle形式で保存します。
# 使用するモデルや特徴量を変更する際は、学習時と推論時で同一の特徴量をモデルに
# 入力するために提出用のpredictor.pyについても変更する必要があることにご注意ください。
# モデルの保存先を指定します。
model_path = "archive/model"
# モデルの種類
models = ["rf"]
# 使用する特徴量カラム
columns = ["fundamental+technical"]
# 目的変数
labels = [
"label_high_20",
"label_low_20",
]
# モデル毎に処理
for model in models:
# 特徴量毎に処理
for col in columns:
# 目的変数毎に処理
for label in labels:
# 学習済みモデルを取得
pred_model = trained_models[model][col][label]
# モデルを保存
save_model(pred_model, label, model_path=model_path)4.predictor.py を記述する
ここでは、提出する予測モデルを読み込み、当該モデルを用いて予測を出力させるコードの書き方について説明します。
predictor.py ファイルには、少なくとも以下のクラス及びメソッドを作成する必要があります。
ScoringService 推論実行のためのクラスです。 以下のメソッドを実装してください。 get_model モデルを取得するメソッドです。以下の条件があります。 - クラスメソッドであること - 引数 model_path (str 型) を指定すること - 正常終了時は返り値を true (bool 型) とすること predict 推論を実行するメソッドです。以下の条件があります。 - クラスメソッドであること - 引数 input (dict[str] 型) を指定すること ※ 詳しくはテンプレート内の、predictor.pyファイルをご確認ください。
本コンペティションにおけるpredictメソッドの返り値の定義は以下となります。詳細は以下に記載したコードをご参照ください。
結果を以下のcsv形式の文字列として出力する。
1列目:datetimeとcodeをつなげたもの(Ex 2016-05-09-1301)
2列目:label_high_20 終値→最高値への変化率
3列目:label_low_20 終値→最安値への変化率
headerはなし、B列C列はfloat64以下は、本チュートリアルで説明した内容をこの規約に合わせて記載したpredictor.pyです。 本コンペティションのPublic LBの評価期間と一致するようにデータの分割期間を調整してあります。
# -*- coding: utf-8 -*-
import io
import os
import pickle
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from tqdm.auto import tqdm
class ScoringService(object):
# 訓練期間終了日
TRAIN_END = "2018-12-31"
# 評価期間開始日
VAL_START = "2019-02-01"
# 評価期間終了日
VAL_END = "2019-12-01"
# テスト期間開始日
TEST_START = "2020-01-01"
# 目的変数
TARGET_LABELS = ["label_high_20", "label_low_20"]
# データをこの変数に読み込む
dfs = None
# モデルをこの変数に読み込む
models = None
# 対象の銘柄コードをこの変数に読み込む
codes = None
@classmethod
def get_inputs(cls, dataset_dir):
"""
Args:
dataset_dir (str) : path to dataset directory
Returns:
dict[str]: path to dataset files
"""
inputs = {
"stock_list": f"{dataset_dir}/stock_list.csv.gz",
"stock_price": f"{dataset_dir}/stock_price.csv.gz",
"stock_fin": f"{dataset_dir}/stock_fin.csv.gz",
# "stock_fin_price": f"{dataset_dir}/stock_fin_price.csv.gz",
"stock_labels": f"{dataset_dir}/stock_labels.csv.gz",
}
return inputs
@classmethod
def get_dataset(cls, inputs):
"""
Args:
inputs (list[str]): path to dataset files
Returns:
dict[pd.DataFrame]: loaded data
"""
if cls.dfs is None:
cls.dfs = {}
for k, v in inputs.items():
cls.dfs[k] = pd.read_csv(v)
# DataFrameのindexを設定します。
if k == "stock_price":
cls.dfs[k].loc[:, "datetime"] = pd.to_datetime(
cls.dfs[k].loc[:, "EndOfDayQuote Date"]
)
cls.dfs[k].set_index("datetime", inplace=True)
elif k in ["stock_fin", "stock_fin_price", "stock_labels"]:
cls.dfs[k].loc[:, "datetime"] = pd.to_datetime(
cls.dfs[k].loc[:, "base_date"]
)
cls.dfs[k].set_index("datetime", inplace=True)
return cls.dfs
@classmethod
def get_codes(cls, dfs):
"""
Args:
dfs (dict[pd.DataFrame]): loaded data
Returns:
array: list of stock codes
"""
stock_list = dfs["stock_list"].copy()
# 予測対象の銘柄コードを取得
cls.codes = stock_list[stock_list["prediction_target"] == True][
"Local Code"
].values
return cls.codes
@classmethod
def get_features_and_label(cls, dfs, codes, feature, label):
"""
Args:
dfs (dict[pd.DataFrame]): loaded data
codes (array) : target codes
feature (pd.DataFrame): features
label (str) : label column name
Returns:
train_X (pd.DataFrame): training data
train_y (pd.DataFrame): label for train_X
val_X (pd.DataFrame): validation data
val_y (pd.DataFrame): label for val_X
test_X (pd.DataFrame): test data
test_y (pd.DataFrame): label for test_X
"""
# 分割データ用の変数を定義
trains_X, vals_X, tests_X = [], [], []
trains_y, vals_y, tests_y = [], [], []
# 銘柄コード毎に特徴量を作成
for code in tqdm(codes):
# 特徴量取得
feats = feature[feature["code"] == code]
# stock_labelデータを読み込み
stock_labels = dfs["stock_labels"]
# 特定の銘柄コードのデータに絞る
stock_labels = stock_labels[stock_labels["Local Code"] == code]
# 特定の目的変数に絞る
labels = stock_labels[label].copy()
# nanを削除
labels.dropna(inplace=True)
if feats.shape[0] > 0 and labels.shape[0] > 0:
# 特徴量と目的変数のインデックスを合わせる
labels = labels.loc[labels.index.isin(feats.index)]
feats = feats.loc[feats.index.isin(labels.index)]
labels.index = feats.index
# データを分割
_train_X = feats[: cls.TRAIN_END]
_val_X = feats[cls.VAL_START : cls.VAL_END]
_test_X = feats[cls.TEST_START :]
_train_y = labels[: cls.TRAIN_END]
_val_y = labels[cls.VAL_START : cls.VAL_END]
_test_y = labels[cls.TEST_START :]
# データを配列に格納 (後ほど結合するため)
trains_X.append(_train_X)
vals_X.append(_val_X)
tests_X.append(_test_X)
trains_y.append(_train_y)
vals_y.append(_val_y)
tests_y.append(_test_y)
# 銘柄毎に作成した説明変数データを結合します。
train_X = pd.concat(trains_X)
val_X = pd.concat(vals_X)
test_X = pd.concat(tests_X)
# 銘柄毎に作成した目的変数データを結合します。
train_y = pd.concat(trains_y)
val_y = pd.concat(vals_y)
test_y = pd.concat(tests_y)
return train_X, train_y, val_X, val_y, test_X, test_y
@classmethod
def get_features_for_predict(cls, dfs, code, start_dt="2016-01-01"):
"""
Args:
dfs (dict) : dict of pd.DataFrame include stock_fin, stock_price
code (int) : A local code for a listed company
start_dt (str): specify date range
Returns:
feature DataFrame (pd.DataFrame)
"""
# stock_finデータを読み込み
stock_fin = dfs["stock_fin"]
# 特定の銘柄コードのデータに絞る
fin_data = stock_fin[stock_fin["Local Code"] == code]
# 特徴量の作成には過去60営業日のデータを使用しているため、
# 予測対象日からバッファ含めて土日を除く過去90日遡った時点から特徴量を生成します
n = 90
# 特徴量の生成対象期間を指定
fin_data = fin_data.loc[pd.Timestamp(start_dt) - pd.offsets.BDay(n) :]
# fin_dataのnp.float64のデータのみを取得
fin_data = fin_data.select_dtypes(include=["float64"])
# 欠損値処理
fin_feats = fin_data.fillna(0)
# stock_priceデータを読み込む
price = dfs["stock_price"]
# 特定の銘柄コードのデータに絞る
price_data = price[price["Local Code"] == code]
# 終値のみに絞る
feats = price_data[["EndOfDayQuote ExchangeOfficialClose"]]
# 特徴量の生成対象期間を指定
feats = feats.loc[pd.Timestamp(start_dt) - pd.offsets.BDay(n) :].copy()
# 終値の20営業日リターン
feats["return_1month"] = feats[
"EndOfDayQuote ExchangeOfficialClose"
].pct_change(20)
# 終値の40営業日リターン
feats["return_2month"] = feats[
"EndOfDayQuote ExchangeOfficialClose"
].pct_change(40)
# 終値の60営業日リターン
feats["return_3month"] = feats[
"EndOfDayQuote ExchangeOfficialClose"
].pct_change(60)
# 終値の20営業日ボラティリティ
feats["volatility_1month"] = (
np.log(feats["EndOfDayQuote ExchangeOfficialClose"])
.diff()
.rolling(20)
.std()
)
# 終値の40営業日ボラティリティ
feats["volatility_2month"] = (
np.log(feats["EndOfDayQuote ExchangeOfficialClose"])
.diff()
.rolling(40)
.std()
)
# 終値の60営業日ボラティリティ
feats["volatility_3month"] = (
np.log(feats["EndOfDayQuote ExchangeOfficialClose"])
.diff()
.rolling(60)
.std()
)
# 終値と20営業日の単純移動平均線の乖離
feats["MA_gap_1month"] = feats["EndOfDayQuote ExchangeOfficialClose"] / (
feats["EndOfDayQuote ExchangeOfficialClose"].rolling(20).mean()
)
# 終値と40営業日の単純移動平均線の乖離
feats["MA_gap_2month"] = feats["EndOfDayQuote ExchangeOfficialClose"] / (
feats["EndOfDayQuote ExchangeOfficialClose"].rolling(40).mean()
)
# 終値と60営業日の単純移動平均線の乖離
feats["MA_gap_3month"] = feats["EndOfDayQuote ExchangeOfficialClose"] / (
feats["EndOfDayQuote ExchangeOfficialClose"].rolling(60).mean()
)
# 欠損値処理
feats = feats.fillna(0)
# 元データのカラムを削除
feats = feats.drop(["EndOfDayQuote ExchangeOfficialClose"], axis=1)
# 財務データの特徴量とマーケットデータの特徴量のインデックスを合わせる
feats = feats.loc[feats.index.isin(fin_feats.index)]
fin_feats = fin_feats.loc[fin_feats.index.isin(feats.index)]
# データを結合
feats = pd.concat([feats, fin_feats], axis=1).dropna()
# 欠損値処理を行います。
feats = feats.replace([np.inf, -np.inf], 0)
# 銘柄コードを設定
feats["code"] = code
# 生成対象日以降の特徴量に絞る
feats = feats.loc[pd.Timestamp(start_dt) :]
return feats
@classmethod
def get_feature_columns(cls, dfs, train_X, column_group="fundamental+technical"):
# 特徴量グループを定義
# ファンダメンタル
fundamental_cols = dfs["stock_fin"].select_dtypes("float64").columns
fundamental_cols = fundamental_cols[
fundamental_cols != "Result_Dividend DividendPayableDate"
]
fundamental_cols = fundamental_cols[fundamental_cols != "Local Code"]
# 価格変化率
returns_cols = [x for x in train_X.columns if "return" in x]
# テクニカル
technical_cols = [
x for x in train_X.columns if (x not in fundamental_cols) and (x != "code")
]
columns = {
"fundamental_only": fundamental_cols,
"return_only": returns_cols,
"technical_only": technical_cols,
"fundamental+technical": list(fundamental_cols) + list(technical_cols),
}
return columns[column_group]
@classmethod
def create_model(cls, dfs, codes, label):
"""
Args:
dfs (dict) : dict of pd.DataFrame include stock_fin, stock_price
codes (list[int]): A local code for a listed company
label (str): prediction target label
Returns:
RandomForestRegressor
"""
# 特徴量を取得
buff = []
for code in codes:
buff.append(cls.get_features_for_predict(cls.dfs, code))
feature = pd.concat(buff)
# 特徴量と目的変数を一致させて、データを分割
train_X, train_y, _, _, _, _ = cls.get_features_and_label(
dfs, codes, feature, label
)
# 特徴量カラムを指定
feature_columns = cls.get_feature_columns(dfs, train_X)
# モデル作成
model = RandomForestRegressor(random_state=0)
model.fit(train_X[feature_columns], train_y)
return model
@classmethod
def save_model(cls, model, label, model_path="../model"):
"""
Args:
model (RandomForestRegressor): trained model
label (str): prediction target label
model_path (str): path to save model
Returns:
-
"""
# tag::save_model_partial[]
# モデル保存先ディレクトリを作成
os.makedirs(model_path, exist_ok=True)
with open(os.path.join(model_path, f"my_model_{label}.pkl"), "wb") as f:
# モデルをpickle形式で保存
pickle.dump(model, f)
# end::save_model_partial[]
@classmethod
def get_model(cls, model_path="../model", labels=None):
"""Get model method
Args:
model_path (str): Path to the trained model directory.
labels (arrayt): list of prediction target labels
Returns:
bool: The return value. True for success, False otherwise.
"""
if cls.models is None:
cls.models = {}
if labels is None:
labels = cls.TARGET_LABELS
for label in labels:
m = os.path.join(model_path, f"my_model_{label}.pkl")
with open(m, "rb") as f:
# pickle形式で保存されているモデルを読み込み
cls.models[label] = pickle.load(f)
return True
@classmethod
def train_and_save_model(
cls, inputs, labels=None, codes=None, model_path="../model"
):
"""Predict method
Args:
inputs (str) : paths to the dataset files
labels (array) : labels which is used in prediction model
codes (array) : target codes
model_path (str): Path to the trained model directory.
Returns:
Dict[pd.DataFrame]: Inference for the given input.
"""
if cls.dfs is None:
cls.get_dataset(inputs)
cls.get_codes(cls.dfs)
if codes is None:
codes = cls.codes
if labels is None:
labels = cls.TARGET_LABELS
for label in labels:
print(label)
model = cls.create_model(cls.dfs, codes=codes, label=label)
cls.save_model(model, label, model_path=model_path)
@classmethod
def predict(cls, inputs, labels=None, codes=None, start_dt=TEST_START):
"""Predict method
Args:
inputs (dict[str]): paths to the dataset files
labels (list[str]): target label names
codes (list[int]): traget codes
start_dt (str): specify date range
Returns:
str: Inference for the given input.
"""
# データ読み込み
if cls.dfs is None:
cls.get_dataset(inputs)
cls.get_codes(cls.dfs)
# 予測対象の銘柄コードと目的変数を設定
if codes is None:
codes = cls.codes
if labels is None:
labels = cls.TARGET_LABELS
# 特徴量を作成
buff = []
for code in codes:
buff.append(cls.get_features_for_predict(cls.dfs, code, start_dt))
feats = pd.concat(buff)
# 結果を以下のcsv形式で出力する
# 1列目:datetimeとcodeをつなげたもの(Ex 2016-05-09-1301)
# 2列目:label_high_20 終値→最高値への変化率
# 3列目:label_low_20 終値→最安値への変化率
# headerはなし、B列C列はfloat64
# 日付と銘柄コードに絞り込み
df = feats.loc[:, ["code"]].copy()
# codeを出力形式の1列目と一致させる
df.loc[:, "code"] = df.index.strftime("%Y-%m-%d-") + df.loc[:, "code"].astype(
str
)
# 出力対象列を定義
output_columns = ["code"]
# 特徴量カラムを指定
feature_columns = cls.get_feature_columns(cls.dfs, feats)
# 目的変数毎に予測
for label in labels:
# 予測実施
df[label] = cls.models[label].predict(feats[feature_columns])
# 出力対象列に追加
output_columns.append(label)
out = io.StringIO()
df.to_csv(out, header=False, index=False, columns=output_columns)
return out.getvalue()モジュールの追加
https://docs.anaconda.com/anaconda/packages/py3.7_linux-64/ この表の [In Installer] にチェックが入っているものが、すでにインストールされています(ただしバージョンは異なります)。
Runtime環境にモジュールを追加するためには requirements.txt に追記します。requirements.txtに記載したモジュールは実行時にpipでインストールされます。
モジュールを追加する際はRuntime環境でインストール及び使用可能かをご確認ください。本チュートリアルで評価のために使用したSHAPのように、一部のモジュールはインストール時にビルドが必要となるものもあります。そのためRuntime環境では使用することのできないモジュールもあります。以下のように実行環境のdocker container内でインストールすることで確認可能です。
$ docker run --rm -it continuumio/anaconda3:2019.03 bash
# pip install tensorflow==2.4.0requirements.txt には以下のようにモジュールのバージョンを指定して記載します。これは、モデルを提出してから全ての評価が完了するまで数ヶ月かかるためその間にモジュールの最新バージョンがリリースされても影響を受けないようにするためです。
tensorflow==2.4.0
requirements.txt の作成には pip freeze コマンドを使用すると便利です。
$ docker run --rm -it continuumio/anaconda3:2019.03 bash
# pip install [インストールするモジュール]
# pip freezeデバッグ方法
通常
$ pip install -r requirements.txt # モジュールが必要な場合は pip でインストールします $ cd src # ソースディレクトリに移動 $ python # python の実行 Python 3.7.3 (default, Mar 27 2019, 16:54:48) [Clang 4.0.1 (tags/RELEASE_401/final)] :: Anaconda, Inc. on darwin Type "help", "copyright", "credits" or "license" for more information. >>> DATASET_DIR= "/path/to" # データ保存先ディレクトリ >>> from predictor import ScoringService # モジュール読み込み >>> inputs = ScoringService.get_inputs(DATASET_DIR) # 推論入力データ取得 >>> ScoringService.get_model() # モデルの取得 True >>> ScoringService.predict(inputs) # 推論の実行 '[推論結果]'
pyenvを使用
$ pyenv local anaconda3-2019.03
以降 通常のインストールの場合と同様のデバッグ方法です。
Docker を使用
$ docker run -it -v $(pwd):/opt/ml continuumio/anaconda3:2019.03 /bin/bash $ cd /opt/ml
以降は、通常のインストールの場合と同様のデバッグ方法になります。
5.zip で圧縮して提出する。
指定されたディレクトリ構成で学習済みモデルを保存した上で、predictor.pyを作成したら、以下のようにzipで圧縮して提出します。
$ ls model requirements.txt src $ zip -v submit.zip requirements.txt src/*.py model/*.pkl updating: requirements.txt (in=0) (out=0) (stored 0%) updating: src/predictor.py (in=11408) (out=2417) (deflated 79%) updating: model/my_model_label_high_20.pkl . (in=18919345) (out=5071005) (deflated 73%) updating: model/my_model_label_low_20.pkl . (in=18704305) (out=5006613) (deflated 73%) total bytes=37635058, compressed=10080035 -> 73% savings
2.13.3. ランタイム環境に関して
■ランタイム環境での利用可能なデータについて
・ランタイム環境に提出したモデルは、各銘柄の株価の最高値及び最安値を予測する際、評価対象となる決算短信の開示日以前のデータ(銘柄、株価、ファンダメンタル情報)を利用することができます。
・ただし、ランタイム環境では、評価対象となる決算短信の開示日の期間のデータを全て格納しているため、予測時に開示日より未来のデータを利用すると、リークが生じることになります。
・ランタイム環境でこれらのデータを用いて特徴量生成やモデルの再学習を行う際は、リークが含まれないようご留意ください。
以下、ランタイム実行日が5月10日のケース(Private 1st)を例として取り上げます。
・ランタイム環境には、2016年1月1日から2021年4月5日までのデータが配置されています ・提出モデルは、3月29日に開示された決算短信について翌営業日より20営業日間の最高値及び最安値を予測する際、3月29日までのデータを利用できます。3月30日以降のデータを利用するとリークとなり、入賞資格を失います ・同様に、4月1日に開示された決算短信について予測する際には、4月2日以降のデータは利用できません
3. ポートフォリオを構築しよう
3.1. 「ニュース分析チャレンジ」のチュートリアルの構成
3章から6章では、J-Quantsで開催するコンペティションのうち、「ニュース分析チャレンジ」に係るチュートリアルを提供します。 本コンペティションでは、2章に記載している「ファンダメンタルズ分析チャレンジ」と同様に、データ分析や株式取引には興味はあるが、きっかけがないという方を主な対象として、投資にまつわるデータ・環 境を提供し、株式市場におけるデータ利活用の可能性を試していただくことを期待しています。
大まかに3章から6章にかけてどのようなことが記載されているのかを以下で説明します。
3.1.1. 3章の概要
3章では本コンペティションに参加するための基本知識を学ぶことができます。主に以下のような題材を扱います。
-
コンペティション課題の説明
-
データセットの説明
-
提出モデルの予測出力の定義
-
バックテスト手法
-
シンプルなポートフォリオの組成方法
-
ポートフォリオの評価方法
-
構築したモデルの提出方法
3.1.2. 4章の概要
4章では本チュートリアルの2章で構築した最高値・最安値モデルを使用したポートフォリオの構築方法を紹介しています。3章では機械学習的な手法を用いていませんが、4章では機械学習的手法で作成したモデルを利用しています。また、本コンペティションで提供されている適時開示情報についても簡単に触れています。3章より内容は複雑になりますが、実際に機械学習をポートフォリオ組成に活かすための知識を学ぶことができます。主に以下のような題材を扱います。
-
2章で作成したモデルの修正
-
モデルを用いたポートフォリオの組成方法
-
適時開示情報の有効活用
3.1.3. 5章の概要
5章では本コンペティションの特色であるニュースデータを活用した取引戦略を構築するための手法を紹介しています。近年のディープニューラルネットワークの研究の発展により、自然言語処理の分野においても大きな技術の発展がありました。5章ではその中でも大きな成果の一つであるBERT(Bidirectional Encoder Representations from Transformers) (参考: 自然言語処理の王様「BERT」の論文を徹底解説) を用いた特徴量抽出手法を紹介しています。 また、ニュースデータの前処理や可視化も丁寧に説明しており、本コンペの特色であるニュースデータの解析に必要な以下のような基礎知識を学ぶことができます。
-
テキストデータの基礎知識
-
テキストデータの前処理方法
-
テキストデータの可視化方法
-
BERTモデルによるニュースデータからの特徴量抽出手法
3.1.4. 6章の概要
6章では5章で取得したBERT特徴量を用いた取引戦略を構築するための手法の一つとしてLSTM(Long Short Term Memory)(参考: LSTMネットワークの概要)を用いたスコア生成手法を紹介しています。ただし、本章はディープニューラルネットワークの基礎知識等を前提とした、かなり高度な内容になっており、少し発展的な内容となります。
3.2. 「ニュース分析チャレンジ」について
本節では、本コンペティションについての概要やスケジュールを記載しています。
コンペティションの課題内容
本コンペティションでは、現金100万円を原資として、ある週の週初営業日に始値で購入、その週の週末営業日に売却するとした場合に、できる限り利益を得るポートフォリオの予測に取り組んでいただきます。
そして、前述の予測を予め決められた4週間の間に4ラウンド行っていただき、その4ラウンド全ての合計の利益を競っていただきます。
コンペティションの概要
| 項目 | 内容 |
|---|---|
コンペティション名 |
ニュース分析チャレンジ |
主な対象者 |
株式市場を対象としたデータ分析の初学者・データサイエンスに知見のある有識者・テキストデータ分析の有識者等 |
入力内容(利用データ) |
銘柄情報・株価情報・ファンダメンタル情報等・日経電子版見出しテキストデータ・適時開示データ |
出力内容(予測対象) |
現金100万円を原資とし、ある週の週初営業日に複数銘柄(最低5銘柄以上)を始値で購入、その週の週末営業日に終値で売却するとした場合のポートフォリオ |
参加を通じて得られる知見 |
- 株価や企業業績の推移などの時系列データの解析手法 |
スケジュール
| 日時 | 内容 |
|---|---|
2021年3月19日(金) |
コンペティション開始(データダウンロードのみ可能、モデル提出は不可) |
2021年3月26日(金) |
モデル提出開始 |
2021年5月9日(日) |
モデル提出締切 |
2021年5月10日(月)〜 6月4日(金) |
モデル評価期間(4週間4ラウンド) |
2021年7月頃 |
入賞者の決定 |
3.3. 予測対象
本節では、本コンペティションの予測対象であるポートフォリオやその構成銘柄の条件等について詳しく説明しています。
予測対象
本コンペティションの予測対象は、現金100万円を原資として、ある週の週初営業日に始値で購入、その週の週末営業日に売却するとした場合に高い利益を得るポートフォリオとなります。下図に最終的な課題内容及び評価についてイメージを示しています。
ポートフォリオとは、「資産運用の世界で様々な資産または銘柄の組み合わせのこと」(引用:JPXHP用語集)を指します。
3.3.1. ポートフォリオに組入れできる銘柄の条件
本コンペティションの予測対象となるポートフォリオを構成する銘柄は、次に挙げる条件を全て満たすものになりますのでご注意ください。
A) 2020年12月末時点で、東京証券取引所に上場していること
B) 普通株式であること(種類株ではないこと)
C) ETF、ETN、REIT、優先出資証券、インフラファンド、外国株のいずれにも該当しないこと
D) 2020年12月末時点で、時価総額が200億を上回っていること
3.3.2. ポートフォリオの条件
本コンペティションの予測対象となるポートフォリオは、次に挙げる条件を全て満たすものになります。条件を満たさないポートフォリオは失格となります。
A) 原資100万円のうち、少なくとも50万円は株の購入に充てられていること(すなわち、原資100万円全てを投資しなくても良く、50万円は銘柄購入に、残り50万円を現金として保有することは可能)
B) 少なくとも5銘柄以上で構成されるポートフォリオであること
3.3.3. 提出するモデルの予測出力の定義
本コンペティションで提出していただくモデルの出力は以下のフォーマット及び条件を満たす必要があります。
出力フォーマット
以下のcsv形式で出力
| 列 | 名前 | 型 | 例 | 説明 |
|---|---|---|---|---|
1列目 |
date |
string |
2021-02-01 |
株を購入する日付(各週の月曜日の日付) |
2列目 |
Local Code |
int64 |
8697 |
銘柄コード |
3列目 |
budget |
int64 |
50000 |
購入金額 |
CSVの出力例を以下に示します。
フォーマットの条件
-
ヘッダが付与されていること
-
5銘柄以上選択されていること
-
dateは予測対象の週の月曜日の日付であること
-
購入金額は1以上であること
-
銘柄を購入優先度順に上から出力すること
-
Nanが含まれないようにすること
特記事項及び注意点
以下では、各条件を踏まえた特記事項及び注意点につきまして、説明します。
-
本コンペティションでは、*各銘柄は1株単位で購入可能* とします。
-
東京証券取引所をはじめとする全国の証券取引所で実際に売買する際は、売買単位は100株単位に統一されていますが、本コンペティションでは、ポートフォリオの組成を可能な限り幅広く行っていたくことを考慮して、売買単位を1株単位としています。
-
-
ポートフォリオに組入れできる銘柄の条件に合致しない銘柄がモデルの予測に含まれている場合は、評価の際に該当のレコードは評価対象外として無視されます。(エラーとはなりません。)
-
モデルの予測においてdate列が週初営業日以外の日付のレコードは、評価対象外として無視されます。
-
Budget列が1未満のレコードは評価対象外として無視されます。
-
週初営業日に値段が付かなかった銘柄*のレコードは評価対象外として無視されます。
※ なお、週末営業日に値段が付かなかった場合には、その日より前の日で終値が存在する日の終値を用います。 -
購入金額が50万円に到達していなかった場合は、選択された銘柄を入力順(テーブルデータの並び順)に1株ずつ50万円以上になるまで買い足されます。(評価時の具体的な処理は3.3.5. 評価方法を参照してください。)
-
購入金額が100万円を超える場合は、100万円以内の範囲で購入可能な株数に調整されます。(評価時の具体的な処理は3.3.5. 評価方法を参照してください。)
-
最終的に購入された銘柄数が5銘柄未満の場合若しくは購入した金額が50万円未満の場合は、エラーとなり失格となります。
3.3.4. 評価方法
本コンペティションでは、モデルで予測したポートフォリオで得られる利益の総合計による定量評価方法を採用します。
まず、各週にポートフォリオから得られる利益を以下の算出式を用いて計算します。
保有している株式の合計評価額 = 保有している株式のその週の週末営業日の終値 × 保持する株数
保持現金 = その週の週初営業日に株式の購入に利用せずに手元に残った現金
その上で、各週の運用実績を合計し、最終スコアとして評価し、利益の高い順に順位付けします。(ただし、利益が全く同じであった場合には、提出が早かった方を上位とします。)
バックテスト関数(backtest.py)の挙動
本コンペティションにおける評価では、チュートリアルレポジトリに配置してある独自のバックテストライブラリ backtest.py を用いています。
モデルにより予測されたポートフォリオについて、具体的な処理の概要は以下のとおりです。なお、詳細な挙動につきましては、実際のコードをご参照ください。
【前提条件チェック等】
1. 予測されたポートフォリオのフォーマットについて以下のチェックを行う(※)。
- date列(ヘッダー)が存在するか
- Local Code列(ヘッダー)が存在するか
- budget列(ヘッダー)が存在するか
- データにNaNが含まれていないか
2. 予測されたポートフォリオのLocal Code列について、「ポートフォリオに組入れできる条件」に合致するレコードに絞り込む。
3. 予測されたポートフォリオのdate列について、月曜日のみのレコードに絞り込む。
4. 予測されたポートフォリオのbudget列について、1円以上のレコードに絞り込む。
【購入処理】
5. 2〜4で絞り込んだポートフォリオについて、5銘柄以上選択されているかチェックを行う(※)。
6. ポートフォリオのLocal Code列の上から順に、原資金100万円を上限として、budget列で指定された金額で購入処理を行う。(なお、各ラウンドの週初営業日の始値で購入するため、指定された金額と実際の購入金額は異なることが想定され、予算と実際の購入金額の差額は残額となります。)
7. 予測されたポートフォリオの全てのレコードについて6の処理を行い、実際の購入金額が50万円未満の場合は、ポートフォリオのLocal Code列の上から順に、更に1株ずつ50万円以上となるまで購入処理を繰り返す。
8. 購入処理後に残った原資金は現金保有とする。
9. 6〜8 までの購入処理を終えたポートフォリオについて、実際に購入した銘柄数が5銘柄以上かつ実際の購入金額が50万円以上かチェックを行う(※)。
【売却処理・評価】
10. 購入した各銘柄について、各ラウンドの週末営業日の終値で売却したこととし、週初営業日からの始値からの運用実績(保有している株式の合計評価額 + 保持現金 - 購入原資金)を算出する。
なお、(※)と記されているチェック項目については、チェックでエラーとなった場合は、評価算出されず失格となりますので、ご注意ください。以下に、Public期間について具体例を用いて処理について例示しております。
以下に、本コンペティションのPublic期間における評価について具体例を用いて処理について例示しております。
上表の左側がモデルが予測したポートフォリオの出力例です。上表の右側は説明のために付け加えたものになります。
・前提条件チェック等の1〜4に従い、条件の確認と銘柄等の絞り込みを行います。
・購入処理の5で5銘柄以上含まれていることを確認し、6の処理により購入を行います。
・ポートフォリオの全てのレコード列を処理した結果、実際の購入金額の総額は474,860円/5銘柄だった(9983の始値が指定してbudgetを超過し購入できていない)ため、7の処理により再度ポートフォリオの上から1株ずつ追加で購入する処理が行われます。具体的には7203を1株購入→50万円check→未達→9984を1株購入→50万円check→未達→9983を1株購入→50万円基準達成(実際の購入金額588,960円/6銘柄、保持現金411,040円)
・6〜8までの処理を終え、9で実際に購入した銘柄数が5銘柄以上及び実際の購入金額が50万円以上かをチェックし、購入処理は完了します。
・最後に購入した銘柄について、そのラウンドの週末営業日の終値で評価し、保持現金と合わせてそのラウンドの運用実績とします。
3.3.5. リーダーボード
一般的に、データ分析コンペティションにおけるリーダーボード(Leaderboard)とは、コンペティション参加者の投稿内容に対する評価(スコア、実行時間等)をランキング形式で並べる表を意味します。本コンペティションで提供するリーダーボードは、パブリックリーダーボード(以下、Public LB)とプライベートリーダーボード(以下、Private LB)の2つで構成されます。以下では、それぞれのリーダーボードの仕様等について説明します。
まず、本コンペティションのPublic LBは、コンペティション開催日より過去の期間を対象として評価を実施します。具体的には、本コンペティションのPublic LBでは、2021年2月1日(月)に始値で購入し、2021年2月5日(金)の終値で売却するとした際に、できる限り利益を得ることができるポートフォリオを予測します。よってPublic LBでは、予測されたポートフォリオで利益の高い順に順位付けされます。
なお、Public LBの評価期間における各銘柄の株価は、各Webサイト等で取得可能であることから、本コンペティションのPublic LBではチーティングが容易であるため、本コンペティションのPublic LBは、他の一般的なコンペティションにおけるPublic LBとは異なり、スコアを競うというよりは、モデルが正常に投稿できることを確認するための環境として位置付けとしておりますので、ご留意ください。以下に、Public LBの評価例として図を示します。
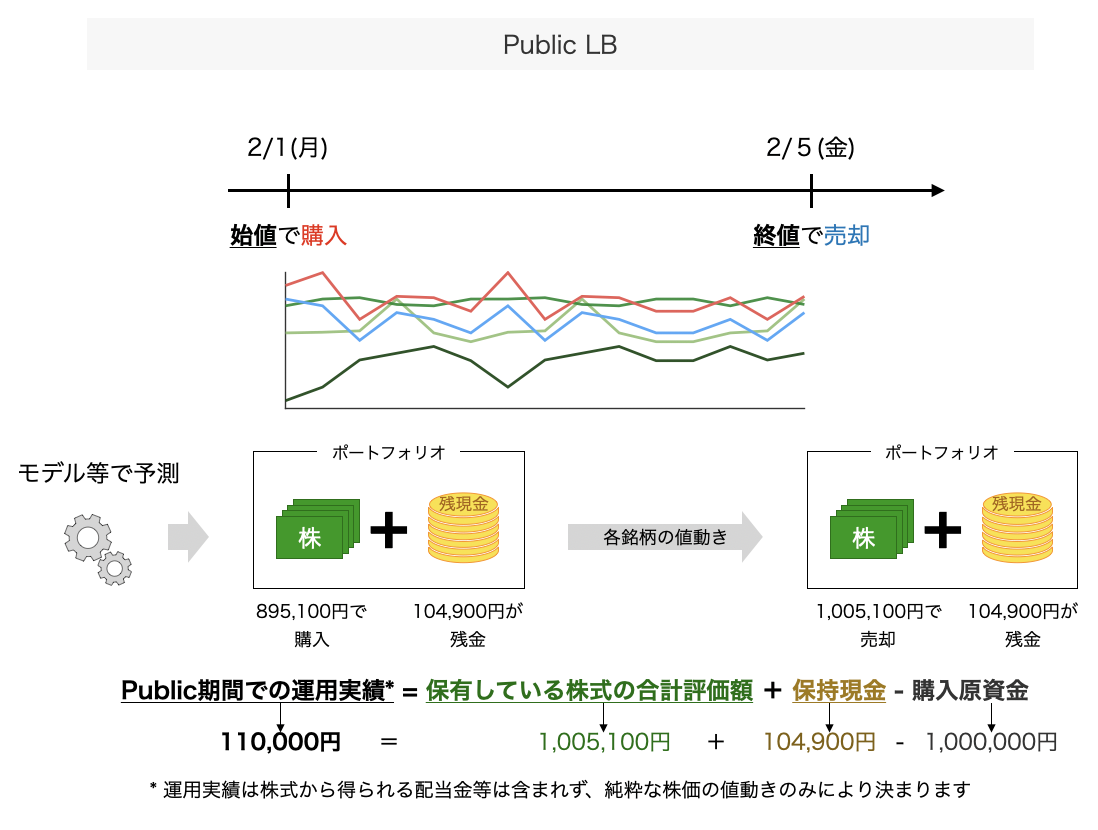
次に、本コンペティションのPrivate LBについて説明します。本コンペティションのPrivate LBでは、リークを可能な限り防止するため、モデル提出締切日よりも将来のデータを用いて、Private LBを出力します。
Private LBの各ラウンドの具体的な評価期間は以下のとおりです。
-
2021年5月10日(月)の始値で購入し、2021年5月14日(金)の終値で売却とした際の運用実績(ラウンド1)
-
2021年5月17日(月)の始値で購入し、2021年5月21日(金)の終値で売却とした際の運用実績(ラウンド2)
-
2021年5月24日(月)の始値で購入し、2021年5月28日(金)の終値で売却とした際の運用実績(ラウンド3)
-
2021年5月31日(月)の始値で購入し、2021年6月 4日(金)の終値で売却とした際の運用実績(ラウンド4)
上記期間における4ラウンドの運用実績を合計し、総利益の高い順に順位付けされます。
以下に、Private LBの評価例として図を示します。
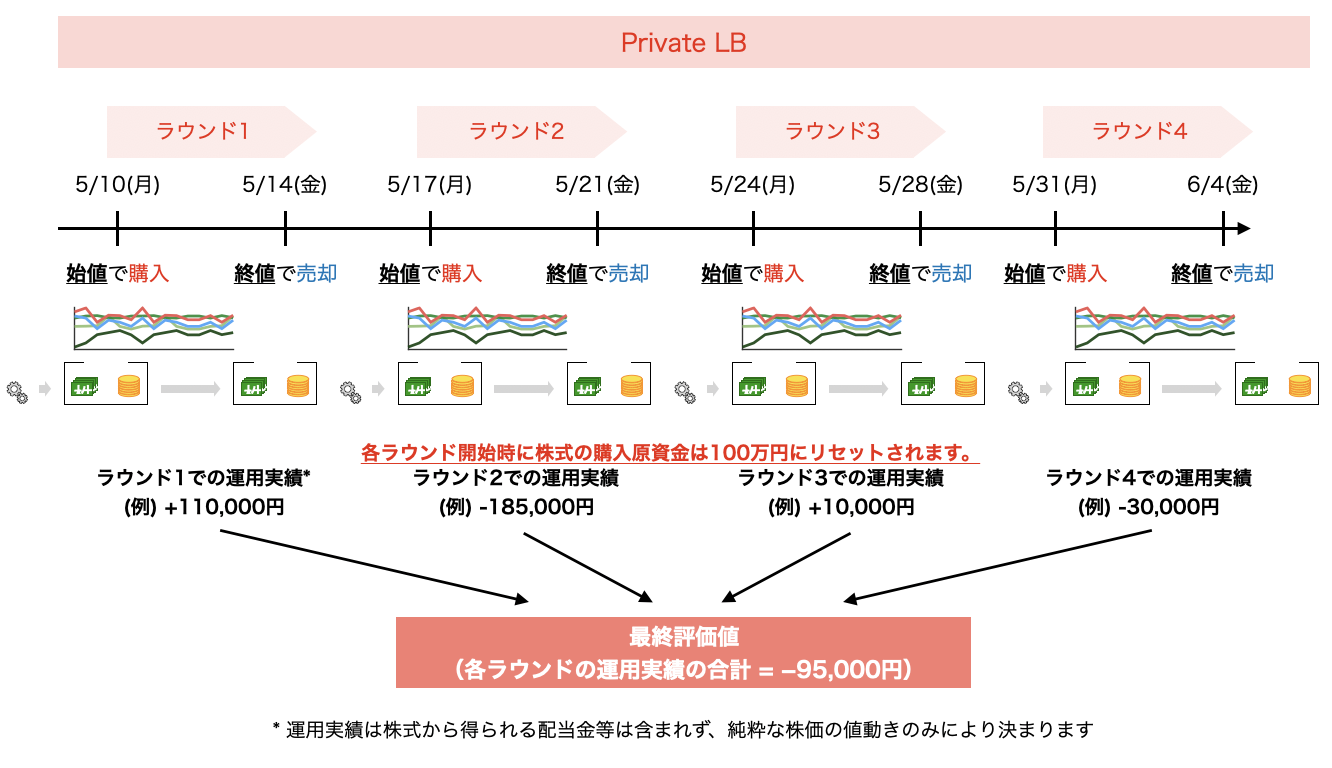
以上を踏まえ、本コンペティションにおけるPublic LBとPrivate LBの概要を、表にまとめます。
本コンペティションにおけるリーダーボードの仕様
| 項目 | Public LB | Private LB |
|---|---|---|
用途 |
モデルが正常に投稿できることを確認するための環境 |
本コンペティションの最終的なランキングを表示 |
予測対象の期間 |
2021年2月1日(月)〜2021年2月5日(金) |
2021年5月10日(月)〜2021年6月4日(金)までの4ラウンド |
予測対象の条件 |
3.3.1及び3.3.2項に示すとおり |
同左 |
予測内容 |
予測対象期間の週初営業日に購入し、当該期間の週末営業日に売却した際にできる限り利益を得るポートフォリオ |
各週の週初営業日に購入し、その週の週末営業日に売却した際にできる限り利益を得るポートフォリオ |
評価方法 |
3.3.3項に示す評価方法 |
3.3.3項に示す評価方法を、4ラウンド行いその合計 |
3.4. データセットの説明
ここでは、本コンペティションで提供している各データについて説明します。提供されるデータは以下の13種類です。
SIGNATEのコンペティションサイトよりダウンロードしてください。
データ概要
| ファイル名 | 説明 |
|---|---|
stock_list |
各銘柄の情報が記録されたデータ ※1 ※2 |
stock_price |
各銘柄の株価情報(始値・高値・安値・終値等)が記録されたデータ ※1 |
stock_fin |
各銘柄のファンダメンタル情報(決算数値データや配当データ等)が記録されたデータ ※1 |
stock_labels |
各銘柄で決算発表が行われた日の取引所公式終値から、その日の翌営業日以降N営業日間における取引所公式終値の最高値および最安値への変化率を記録したデータ ※1 |
stock_fin_price |
データが扱いやすいようにstock_price及びstock_finをマージしたデータ ※1 |
nikkei_article |
日経電子版見出し・メタデータ *3 |
article |
日経電子版見出し・メタデータの分類語 記事種別 |
industry |
日経電子版見出し・メタデータの分類語 業界コード |
industry2 |
日経電子版見出し・メタデータの分類語 業界コード(PDコード) |
region |
日経電子版見出し・メタデータの分類語 地域 |
theme |
日経電子版見出し・メタデータの分類語 記事内容のテーマコード |
tdnet |
適時開示資料のメタデータ (API経由でPDFを取得可能 ※4) |
disclosureItems |
適時開示資料の公開項目コード |
headline_features.pkl |
本チュートリアルの5章で作成したヘッドラインの特徴量をpkl化したファイル |
keywords_features.pkl |
本チュートリアルの5章で作成したキーワードの特徴量をpkl化したファイル |
headline_features.zip |
本チュートリアルの6章で作成したヘッドラインの特徴量及びsentiment scoreをpkl化したファイル |
keywords_features.zip |
本チュートリアルの6章で作成したキーワードの特徴量及びsentiment scoreをpkl化したファイル |
purchase_date.csv |
評価対象週における 初日の日付を指定するファイル |
提供データについては、一部データを除き2016年1月初から2020年12月末をcsvファイル形式、2021年1月初からのデータについては、本コンペティション専用のAPIにて提供いたします。APIによるデータ取得につきましては、8章をご参照ください。
※1 ファンダメンタルズ分析チャレンジと共通の5種類のデータについては「2.2. データセットの説明」をご参照ください。
※2 stock_listについては、ニュース分析チャレンジでは「universe_comp2」という列が追加されているため、以下に説明を記載しています。
*3 当該データについては、2020年以降のデータとなります。
※4 PDFのファイル取得は、2020年1月以降のものが対象です。ランタイム環境ではPDF/XBRLの提供はございません。
3.4.1. 銘柄情報: stock_list
stock_listは、基本的にはファンダメンタルズ分析チャレンジと共通となりますが、ニュース分析チャレンジの予測対象銘柄を判別するための「universe_comp2」というカラムが追加されています。本コンペティションではポートフォリオに「universe_comp2」が True と設定されている銘柄のみを組み入れる必要があります。
ポートフォリオに予測対象銘柄以外を組み入れた場合は、その銘柄についての購入指示は無視されて評価対象外となります。
| 変数名 | 説明 | 型 | 例 |
|---|---|---|---|
prediction_target |
予測対象銘柄 |
bool |
True |
Effective Date |
銘柄情報の基準日 |
int64 |
20201030 |
Local Code |
株式銘柄コード |
int64 |
1301 |
Name (English) |
銘柄名 |
object |
KYOKUYO CO.,LTD. |
Section/Products |
市場・商品区分 |
object |
First Section (Domestic) |
33 Sector(Code) |
銘柄の33業種区分(コード) |
int64 |
50 |
33 Sector(name) |
銘柄の33業種区分(名前) |
object |
Fishery, Agriculture and Forestry |
17 Sector(Code) |
銘柄の17業種区分(コード) |
int64 |
1 |
17 Sector(name) |
銘柄の17業種区分(名前) |
object |
FOODS |
Size Code (New Index Series) |
TOPIXニューインデックスシリーズ規模区分(コード) |
object |
7 |
Size (New Index Series) |
TOPIXニューインデックスシリーズ規模区分 |
object |
TOPIX Small 2 |
IssuedShareEquityQuote AccountingStandard |
会計基準 単独:NonConsolidated、連結国内:ConsolidatedJP、連結SEC:ConsolidatedUS、連結IFRS:ConsolidatedIFRS |
object |
ConsolidatedJP |
IssuedShareEquityQuote ModifyDate |
更新日 |
object |
2020/11/06 |
IssuedShareEquityQuote IssuedShare |
発行済株式数 |
float64 |
10928283.0 |
universe_comp2 |
ニュース分析チャレンジの予測対象銘柄 |
bool |
True |
(JPX東証上場銘柄一覧より引用 https://www.jpx.co.jp/markets/statistics-equities/misc/01.html)
(Quick xignite API Market Data API Catalogより引用 https://www.marketdata-cloud.quick-co.jp/Products/)
3.4.2. 日経電子版見出し・メタデータ: nikkei_article
nikkei_articleでは、日経電子版の見出しおよびメタデータを提供しています。記事見出しやキーワードなどの言語データに加え、一部のレコードには該当の記事に関連する株式コードや、記事の分類情報が含まれています。分類情報については別途CSVファイルでも提供しておりますのでご参照ください。
| 変数名 | 説明 | 型 | 例 |
|---|---|---|---|
article_id |
記事ID(DBユニークキー) |
object |
TDSKDBDGXMZO5518670003022020QM8000 |
publish_datetime |
"掲載日(datetime型)""2016-09-25T23:33:26Z"" など ※新聞各紙の時分は00:00:00固定" |
object |
2020-02-03T17:58:25+09:00 |
media_code |
"媒体略号 媒体のユニークコード ・日本経済新聞朝刊:NKM、NK2、NK3、NK4、NK5、NK6 ・日本経済新聞夕刊:NKE ・日本経済新聞地方経済面:NKL ・日経産業新聞:NSS、SS2・日経MJ:NRS、RS2 ・日経速報ニュースアーカイブ:NKR" |
object |
NKE |
media_name |
"媒体名称 ""日本経済新聞 朝刊""、""日経速報ニュースアーカイブ""など" |
object |
日本経済新聞電子版 |
men_name |
"面名 地方経済面の場合に収録。""名古屋朝刊社会面""、""埼玉”など" |
object |
名古屋朝刊社会面 |
page_from |
"検索掲載開始ページ掲載ページ。但し、地方経済面のページ情報は、掲載されたページではなく、どの地方の記事であるかを意味する。※対応表参照" |
object |
|
picture_flag |
"絵・写真・表の有無”” or ”有”" |
object |
有 |
paragraph_cnt |
"記事本文段落数" |
int64 |
2 |
char_length |
"記事本文文字数" |
int64 |
221 |
headline |
"記事見出し" |
object |
東商取の売買高、1月は10%増、4カ月ぶり前年越え |
keywords |
"キーワード 記事の文中から主題語として切り出したワード(またはその正式名称)" |
object |
東京商品取引所\n売買高\n前年\n日本取引所グループ\n同月 |
classifications |
"分類情報 記事内容のテーマコード(#W〜)・業界コード(#B〜)、証券コード等の会社コード(T〜、N〜、PD〜)、紙 面名等の記事分類キーワード($〜)、コラム名(「〜」)" |
object |
$絵写表記事\nT8697\nPD521\nN0040431\nN0075107 |
company_g.stock_code |
株式コード |
object |
8697 |
日経電子版見出し・メタデータの確認
ここでは「日経電子版見出し・メタデータ」を把握するために、データを確認していきます。データの確認に使用したnotebookは「handson/Chapter03/20210415_chapter03_news_data_visualization.ipynb」に配置しています。必要に応じてご参照ください。
データを読み込みます。
# 入力パラメーターを設定します。ランタイム環境での実行時と同一フォーマットにします
inputs = {
"stock_list": f"{dataset_dir}/stock_list.csv.gz",
"nikkei_article": f"{dataset_dir}/nikkei_article.csv.gz",
}
# 銘柄リストを取得
df_stock_list = pd.read_csv(inputs["stock_list"])
# 投資対象銘柄を取得
stock_codes = df_stock_list.loc[df_stock_list.loc[:, "universe_comp2"] == True, "Local Code"]
# 日経電子版見出し・メタデータ読み込み
df_nikkei_article = pd.read_csv(inputs["nikkei_article"])
# インデックスを記事の掲載日に設定
df_nikkei_article.set_index("publish_datetime", inplace=True)
# インデックスを日付型に変換
df_nikkei_article.index = pd.to_datetime(df_nikkei_article.index)
# インデックスで安定ソート
df_nikkei_article.sort_index(kind="mergesort", inplace=True)データの件数を確認します。
# 件数を確認
df_nikkei_article.info()出力
<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 178393 entries, 2020-01-01 00:00:00+09:00 to 2020-12-31 23:26:35+09:00
Data columns (total 12 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 article_id 178393 non-null object
1 media_code 178393 non-null object
2 media_name 178393 non-null object
3 men_name 0 non-null float64
4 page_from 0 non-null float64
5 picture_flag 75294 non-null object
6 paragraph_cnt 178393 non-null int64
7 char_length 178393 non-null int64
8 headline 178393 non-null object
9 keywords 177894 non-null object
10 classifications 173346 non-null object
11 company_g.stock_code 68369 non-null object
dtypes: float64(2), int64(2), object(8)
memory usage: 17.7+ MB上記からデータの件数とデータの範囲がわかったので、より具体的な値を把握するために先頭の1レコードを出力します。
# データの開始日と内容を確認
df_nikkei_article.head(1).T
データの最終行を表示します。
# データの最終日を確認
df_nikkei_article.tail(1).T
記事の見出しである headline 列の文字数の分布をプロットします。
# 見出しの文字数の分布をプロット
df_nikkei_article.headline.str.len().hist(figsize=(10,10), bins=50)
記事の見出しは25文字がピークであることを確認できます。
company_g.stock_code 列にはニュースに関連する銘柄コードが含まれています。銘柄コードが含まれているデータを確認します。
# 銘柄コードが含まれているデータを確認
df_nikkei_article.loc[~df_nikkei_article.loc[:, "company_g.stock_code"].isnull()].head().T
一つのニュース記事について「\n」を区切り文字として複数の銘柄コードが格納されていることがわかります。
1週間毎のニュースの記事件数と銘柄コードが含まれている記事の件数をプロットするためのデータを作成します。
# 月曜日を開始日として、週次の記事件数と銘柄コードを含む記事件数を取得
df_weekly_count = df_nikkei_article.resample("W-MON", label="left", closed="left")[["article_id", "company_g.stock_code"]].count()
# 集計内容を確認
df_weekly_count.head(3)
1週間毎の記事件数の統計量を確認します。
# 週次件数の統計量を確認
df_weekly_count.describe()
1週間毎の記事件数の平均は3,300件超、銘柄コードが含まれている記事件数の平均は1,200件超であることがわかります。
次に、1週間毎の記事件数の分布を確認します。
# 週次件数の分布を確認
df_weekly_count.hist(figsize=(20, 10), alpha=0.5, bins=25)
1週間毎の記事件数の推移をプロットします。
# プロット
ax = df_weekly_count.plot(figsize=(20, 8))
# グリッド設定
ax.grid(True)
データの始点・終点では月曜日を起点としているため曜日の数が十分でないこと、5,7,8,9月は祝日が影響して記事件数が少なくなっているようです。
ここからは記事に紐付けられている銘柄コードについて確認します。 記事データから抽出した銘柄コード毎に記事件数をプロットします。ここでは対象とする銘柄コードを投資対象銘柄に限定して確認します。
# 記事に記載されている銘柄コードを取得
s_stocks = df_nikkei_article.loc[~df_nikkei_article.loc[:, "company_g.stock_code"].isnull(), "company_g.stock_code"].str.split("\n")
# 銘柄コード別の件数を取得し、記事件数の多い順にソート
s_stock_counts = pd.Series(Counter(chain.from_iterable(s_stocks))).sort_values(ascending=False)
# 投資対象銘柄に絞り込み
s_stock_counts = s_stock_counts.loc[s_stock_counts.index.astype(int).isin(stock_codes)]
# データフレームに変換して、インデックスをリセット
df_stock_counts = s_stock_counts.to_frame().reset_index(drop=True)
# カラム名を設定
df_stock_counts.rename(columns={0: "article_count"}, inplace=True)
# 投資対象銘柄全体におけるdisclosureItems別の件数の割合を算出
df_stock_counts.loc[:, "percentage"] = (df_stock_counts["article_count"] / df_stock_counts["article_count"].sum()) * 100
# 件数割合の累積を計算
df_stock_counts.loc[:, "cumulative_percentage"] = df_stock_counts["percentage"].cumsum()
# 投資対象銘柄コード別の件数をプロット (全銘柄)
ax = df_stock_counts[["article_count"]].plot(figsize=(20, 8))
# グリッド設定
ax.grid(True)
# 凡例を左上に表示
ax.legend(loc="upper left")
# 2つ目のy軸を作成
ax2 = ax.twinx()
# 開示件数割合の累積をプロット
df_stock_counts[["cumulative_percentage"]].reset_index(drop=True).plot(ax=ax2, color="orange")
# 凡例を右上に表示
ax2.legend(loc="upper right")
x軸は銘柄の数を示しています。青色線は左側のy軸に対応しており記事件数を表しています、黄色線は右側のy軸に対応しており記事件数全体における累積割合を示しています。一部の銘柄に記事件数が集中しており、約1750銘柄中250銘柄で記事件数全体の70%程度を占めていることがわかります。
記事件数の多い順に上位50銘柄をプロットします。
# 投資対象銘柄コード別の記事件数 (件数上位50銘柄)
ax = s_stock_counts.head(50).plot.bar(figsize=(20, 8))
# グリッド設定
ax.grid(True)
7203 のトヨタ自動車、および 9984 のソフトバンクグループに関する記事件数が突出しており、以後記事件数が減少していることがわかります。ニュースの件数は銘柄ごとにかなり偏っていることがわかります。
3.4.3. 日経電子版見出し・メタデータの分類語 記事種別: article
articleでは、日経電子版見出し・メタデータの分類情報(classifications)に記載の記事種類の項目一覧を提供しています。
| 変数名 | 説明 | 型 | 例 |
|---|---|---|---|
code |
分類情報コード |
object |
#K1 |
article |
記事種類項目 |
object |
人事記事 |
3.4.4. 日経電子版見出し・メタデータの分類語 業界コード: industry
industryでは、日経電子版見出し・メタデータの分類情報に記載の業界一覧を提供しています。
| 変数名 | 説明 | 型 | 例 |
|---|---|---|---|
code |
分類情報コード |
object |
#B0010 |
industry1 |
業界項目一覧の大項目 |
object |
資源・エネルギー |
industry2 |
業界項目一覧の小項目 |
object |
石油・鉱業・エネルギー |
3.4.5. 日経電子版見出し・メタデータの分類語 業界コード(PDコード): industry2
industry2では、日経電子版見出し・メタデータの分類情報の業界(PDコード)一覧を提供しています。
| 変数名 | 説明 | 型 | 例 |
|---|---|---|---|
pdcode |
分類情報 |
object |
PD011 |
Industry |
業界項目一覧 |
object |
飼料 |
3.4.6. 日経電子版見出し・メタデータの分類語 地域: region
regionでは、日経電子版見出し・メタデータの分類情報の地域一覧を提供しています。
| 変数名 | 説明 | 型 | 例 |
|---|---|---|---|
code |
分類情報 |
object |
#A700 |
category1 |
地域一覧の大項目 |
object |
外国 |
category2 |
地域一覧の小項目 |
object |
インド |
3.4.7. 日経電子版見出し・メタデータの分類語 記事内容のテーマコード: theme
themeでは、日経電子版見出し・メタデータの分類情報のテーマ一覧を提供しています。
| 変数名 | 説明 | 型 | 例 |
|---|---|---|---|
code |
分類情報 |
object |
#W10101 |
category1 |
テーマ一覧の大項目 |
object |
企業 |
category2 |
テーマ一覧の中項目 |
object |
事業組み替え |
category3 |
テーマ一覧の小項目 |
object |
事業組み替え |
3.4.8. 適時開示資料のメタデータ: tdnet
tdnetでは、適時開示資料のメタデータを提供しています。適時開示資料については「2.1.5. 決算短信・財務諸表」をご参照ください。「disclosureItems (公開項目コード)」の一覧は別途csvファイルで提供しています。
| 変数名 | 説明 | 型 | 例 |
|---|---|---|---|
datetime |
開示日付および開示番号 |
object |
2016-02-19:16:00:00#20160210412154 |
disclosedDate |
開示日付 |
object |
2016-02-19 |
disclosedTime |
開示時刻 |
object |
16:00:00 |
disclosureNumber |
開示番号 |
int64 |
20160210412154 |
code |
銘柄コード |
int64 |
79860 |
name |
銘柄略称 |
object |
J-日本アイエスケイ |
disclosureItems |
公開項目コード |
object |
["11301"] |
title |
表題 |
object |
平成27年12月期 決算短信〔日本基準〕(連結) |
handlingType |
取扱属性 |
object |
null |
modifiedHistory |
開示履歴番号 |
int64 |
1 |
pdfGeneralFlag |
全文情報PDFファイル存在フラグ |
int64 |
1 |
pdfSumaryFlag |
サマリ情報PDFファイル存在フラグ |
int64 |
1 |
xbrlFlag |
XBRL関連ファイル存在フラグ |
int64 |
1 |
適時開示資料のメタデータの確認
ここでは「適時開示資料のメタデータ」を把握するために、データを確認していきます。データの確認に使用したnotebookは「handson/Chapter03/20210415_chapter03_news_data_visualization.ipynb」に配置しています。必要に応じてご参照ください。
データを読み込みます。
# 入力パラメーターを設定します。ランタイム環境での実行時と同一フォーマットにします
inputs = {
"stock_list": f"{dataset_dir}/stock_list.csv.gz",
"nikkei_article": f"{dataset_dir}/nikkei_article.csv.gz",
"disclosureItems": f"{dataset_dir}/disclosureItems.csv.gz",
}
# 銘柄リストを取得
df_stock_list = pd.read_csv(inputs["stock_list"])
# 投資対象銘柄を取得
stock_codes = df_stock_list.loc[df_stock_list.loc[:, "universe_comp2"] == True, "Local Code"]
# 適時開示資料のメタデータ読み込み
df_tdnet = pd.read_csv(inputs["tdnet"])
# インデックスを開示日時に設定
df_tdnet.index = pd.to_datetime(df_tdnet["disclosedDate"].astype(str) + " " + df_tdnet["disclosedTime"])
# インデックスで安定ソート
df_tdnet.sort_index(kind="mergesort", inplace=True)
# 公開項目コード一覧を読み込み
df_disclosureitems = pd.read_csv(inputs["disclosureItems"])データの件数を確認します。
# 件数を確認
df_tdnet.info()出力
<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 510962 entries, 2016-01-12 08:00:00 to 2020-12-30 21:00:00
Data columns (total 13 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 datetime 510962 non-null object
1 disclosedDate 510962 non-null object
2 disclosedTime 510962 non-null object
3 disclosureNumber 510962 non-null int64
4 code 510962 non-null int64
5 name 510962 non-null object
6 disclosureItems 510962 non-null object
7 title 510962 non-null object
8 handlingType 1694 non-null object
9 pdfGeneralFlag 510962 non-null int64
10 modifiedHistory 510962 non-null int64
11 pdfSumaryFlag 510962 non-null int64
12 xbrlFlag 510962 non-null int64
dtypes: int64(6), object(7)
memory usage: 54.6+ MB上記からデータの件数とデータの範囲がわかったので、より具体的な値を把握するために先頭の1レコードを出力します。
# データの開始日と内容を確認
df_tdnet.head(1).T
データの最終行を表示します。
# データの最終日を確認
df_tdnet.tail(1).T
データを加工して解析しやすくします。
# 銘柄コードを4桁に変更
df_tdnet.loc[:, "stock_code"] = df_tdnet.loc[:, "code"].astype(str).str[:4].astype(int)
# 投資対象銘柄に絞り込み
filter_universe = df_tdnet.loc[:, "stock_code"].isin(stock_codes)
# 月曜日を開始日として、投資対象銘柄の週次の件数を取得
df_tdnet_weekly_count = df_tdnet.loc[filter_universe].resample("W-MON", label="left", closed="left")[["disclosureNumber"]].count()
# 集計内容を確認
df_tdnet_weekly_count.head(3)
週毎の開示件数をプロットします。
# プロット
ax = df_tdnet_weekly_count.plot(figsize=(20, 8))
# グリッド設定
ax.grid(True)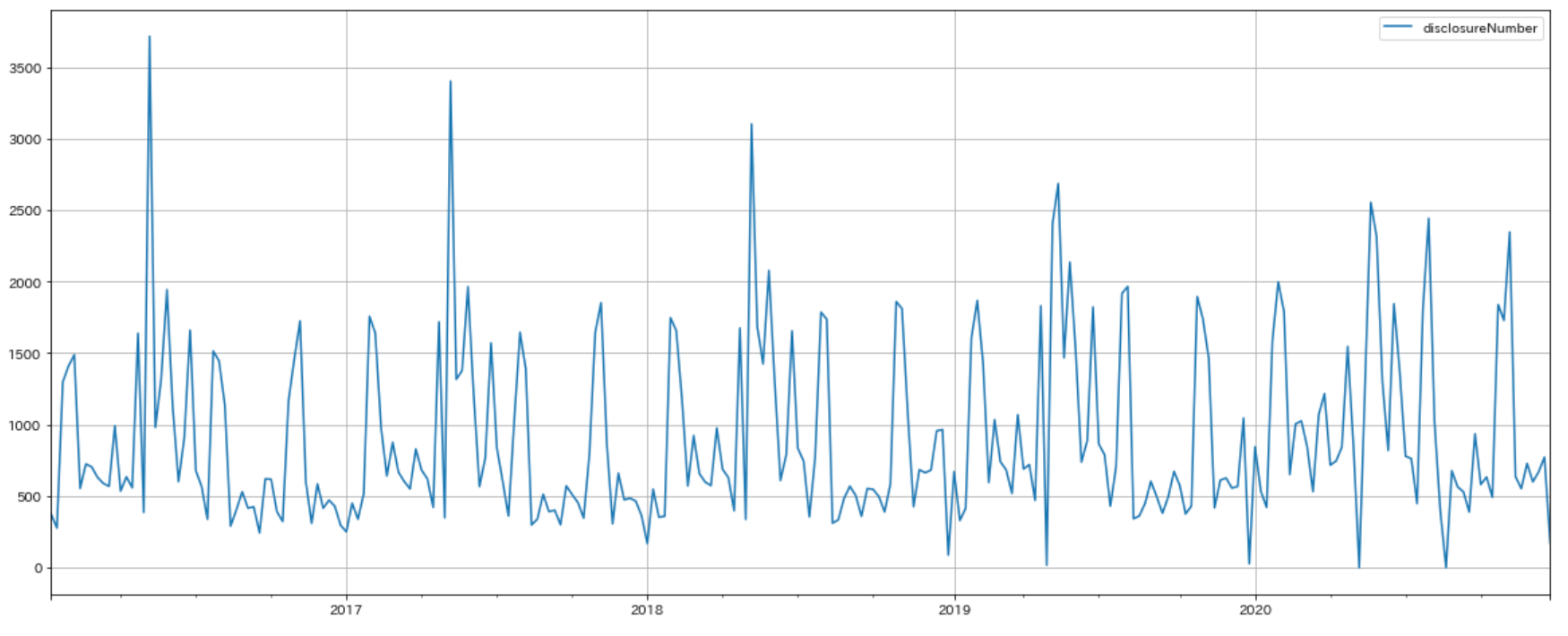
開示件数には波があることがわかります。
週毎の開示件数の分布をプロットします。
# 資対象銘柄の週次件数の分布を確認
df_tdnet_weekly_count.hist(figsize=(10, 10))
開示情報の公開項目コードについて確認していきます。
まずは、公開項目コードをリストとして取得します。
# 投資対象銘柄のdisclosureItemsをリスト形式のシリーズとして取得
s_disclosureItems = df_tdnet.loc[filter_universe, "disclosureItems"].apply(literal_eval)
# データを確認
s_disclosureItems[:10]
次に、公開項目毎の件数を集計したあとに、公開項目コードと日本語名を結合します。
# 投資対象銘柄のdisclosureItems別の件数を取得
s_disclosureitems_count = pd.Series(Counter(chain.from_iterable(s_disclosureItems)))
# カラム名を設定
s_disclosureitems_count.name = "disclosureItems_count"
# 公開項目コードをint型に変更
s_disclosureitems_count.index = s_disclosureitems_count.index.astype(int)
# 項目の日本語名を表示するために適時開示資料の公開項目コードと結合
df_disclosureitems_with_label = pd.merge(s_disclosureitems_count, df_disclosureitems, left_index=True, right_on=["公開項目コード"])
# indexを設定
df_disclosureitems_with_label.set_index("コード値定義", inplace=True)
# 項目の日本語名を表示するために適時開示資料の公開項目コードと結合
df_disclosureitems_with_label = pd.merge(s_disclosureitems_count, df_disclosureitems, left_index=True, right_on=["公開項目コード"])
# indexを設定
df_disclosureitems_with_label.set_index("コード値定義", inplace=True)公開項目コード毎の開示情報件数をプロットします。
# 投資対象銘柄のdisclosureItems別の件数を多い順に並び替え
df_count_by_disclosureitems_with_label = df_disclosureitems_with_label.loc[:, ["disclosureItems_count"]].sort_values("disclosureItems_count", ascending=False).reset_index(drop=True)
# 投資対象銘柄全体におけるdisclosureItems別の件数の割合を算出
df_count_by_disclosureitems_with_label.loc[:, "percentage"] = (df_count_by_disclosureitems_with_label["disclosureItems_count"] / df_count_by_disclosureitems_with_label["disclosureItems_count"].sum()) * 100
# 件数割合の累積を計算
df_count_by_disclosureitems_with_label.loc[:, "cumulative_percentage"] = df_count_by_disclosureitems_with_label["percentage"].cumsum()
# プロット (全て)
ax = df_count_by_disclosureitems_with_label[["disclosureItems_count"]].plot(figsize=(20, 8))
# グリッド設定
ax.grid(True)
# 凡例を左上に表示
ax.legend(loc="upper left")
# 2つ目のy軸を作成
ax2 = ax.twinx()
# 開示件数割合の累積をプロット
df_count_by_disclosureitems_with_label[["cumulative_percentage"]].reset_index(drop=True).plot(ax=ax2, color="orange")
# 凡例を右上に表示
ax2.legend(loc="upper right")
件数の多い上位50項目を公開項目名をX軸にしてプロットします。
# 投資対象銘柄のdisclosureItems別に件数を多い順にプロット (上位50項目)
ax = df_disclosureitems_with_label.loc[:, ["disclosureItems_count"]].sort_values("disclosureItems_count", ascending=False).head(50).plot(kind="bar", figsize=(20, 8))
# グリッド設定
ax.grid(True)
銘柄毎に開示情報の件数をプロットします。
# 投資対象銘柄別に開示件数を集計して、開示件数の多い順に並び替え
df_tdnet_count_by_stock_code = df_tdnet.loc[filter_universe].groupby("stock_code")[["disclosureNumber"]].count().sort_values("disclosureNumber", ascending=False)
# 投資対象銘柄全体における開示件数の割合を集計
df_tdnet_count_by_stock_code.loc[:, "percentage"] = (df_tdnet_count_by_stock_code["disclosureNumber"] / df_tdnet_count_by_stock_code["disclosureNumber"].sum()) * 100
# 開示件数割合の累積を計算
df_tdnet_count_by_stock_code.loc[:, "cumulative_percentage"] = df_tdnet_count_by_stock_code["percentage"].cumsum()
# 投資対象銘柄別に開示件数を多い順にプロット
ax = df_tdnet_count_by_stock_code[["disclosureNumber"]].reset_index(drop=True).plot(figsize=(20, 8))
# グリッド設定
ax.grid(True)
# 凡例を左上に表示
ax.legend(loc="upper left")
# 2つ目のy軸を作成
ax2 = ax.twinx()
# 開示件数割合の累積をプロット
df_tdnet_count_by_stock_code[["cumulative_percentage"]].reset_index(drop=True).plot(ax=ax2, color="orange")
# 凡例を右上に表示
ax2.legend(loc="upper right")
開示件数の多い上位50銘柄をプロットします。
# 投資対象銘柄別に開示件数を多い順にプロット (上位50銘柄)
ax = df_tdnet.loc[filter_universe].groupby("stock_code")[["disclosureNumber"]].count().sort_values("disclosureNumber", ascending=False).head(50).plot(kind="bar", figsize=(20, 8))
# グリッド設定
ax.grid(True)
3.4.9. 適時開示資料の公開項目コード: disclosureItems
disclosureItemsは、適時開示資料の公開項目が含まれています。例えば、一般に「自己株式の取得」はポジティブなイベント、「災害に起因する損害又は業務遂行の過程で生じた損害」はネガティブなイベントとして認識されます。
| 変数名 | 説明 | 型 | 例 |
|---|---|---|---|
分類 |
分類番号 |
int64 |
11 |
公開項目番号 |
公開項目番号 |
int64 |
102 |
公開項目コード |
公開項目コード |
int64 |
11102 |
コード値定義 |
内容説明 |
object |
発行登録及び需要状況調査の開始 |
3.4.10. ニュース記事ヘッドライン特徴量: headline_features.pkl
headline_features.pklは、本チュートリアルの5章で作成したヘッドラインの特徴量をpkl化したファイルです。詳細は本チュートリアルの5.8.4をご参照ください。
3.4.11. ニュース記事キーワード特徴量: keywords_features.pkl
keywords_features.pklは、本チュートリアルの5章で作成したキーワードの特徴量をpkl化したファイルです。詳細は本チュートリアルの5.8.4をご参照ください。
3.4.12. ニュース記事ヘッドライン特徴量(LSTM): headline_features.zip
headline_features.zipは、本チュートリアルの6章で作成したヘッドラインの特徴量及びsentiment scoreをpkl化したファイルです。詳細は本チュートリアルの6.2.9. 特徴量合成モデルの学習及び特徴量合成をご参照ください。
3.4.13. ニュース記事キーワード特徴量(LSTM): keywords_features.zip
keywords_features.zipは、本チュートリアルの6章で作成したキーワードの特徴量及びsentiment scoreをpkl化したファイルです。詳細は本チュートリアルの6.2.9. 特徴量合成モデルの学習及び特徴量合成をご参照ください。
3.4.14. 日付指定ファイル: purchase_date.csv
評価対象週について、初日の日付を指定するファイルです。ランタイム環境ではこのファイルから日付を取得してポートフォリオを作成します。その際に株価データなどは指定された日付のデータを含んでいない点に注意が必要です。例えば、purchase_dateに 2021/02/01 が指定されている場合、stock_priceデータの最も日付の新しいデータは 2021/01/29 になります。そのため、本チュートリアルでは主に金曜日の日付を使用して予測を出力した後、予測からポートフォリオを組成する際に対象日付が翌週の月曜日となるように調整しています。
| 変数名 | 説明 | 型 | 例 |
|---|---|---|---|
purchase date |
評価対象週の初日の日付 |
object |
2021/02/01 |
3.5. 環境構築
3.5.1. 実行環境の選択
環境構築方法については SIGNATE: Runtime 投稿方法: ローカル開発環境の構築方法は? にも説明がありますが、本コンペの特色を考慮し、実行環境の選択方法を説明します。
3章・4章のチュートリアルではDockerとGoogle Colaboratoryの両方を利用可能です。特にWindows環境をご利用でDocker環境の構築が難しい場合は、ぜひGoogle Colaboratoryをご利用ください。本チュートリアルで提供されるnotebookはGoogle Colaboratoryでも動作可能となっております。*なお、Google Colaboratoryをご利用になる場合には、以下のように各ライブラリのバージョンを指定する必要がございます。*
joblib==1.0.1 numpy==1.19.5 pandas==1.1.5 scikit-learn==0.20.3 scipy==1.2.1 seaborn==0.9.0
5章・6章で提供しているnotebookを最後まで実行する場合、ディープニューラルネットワークの学習・推論を行うため、*CPU環境ではかなり時間がかかります。そのため、GPU環境での実行をおすすめしております。* なお、Google ColaboratoryではGPU環境がご利用いただけますので、GPU環境をお持ちでない場合はGoogle Colaboratoryをご利用ください。
3.5.2. Google Colaboratoryをご利用の場合
本コンペティションの3章、4章のチュートリアルをGoogle Colaboratory上で動かすためには、まず以下の手順でGoogle Drive上にファイルを設置します。
-
Google DriveのMy Driveに
JPX_competitionというフォルダーを作成します。 -
1で作成した
JPX_competitionフォルダーにデータを保存するためのdata_dir_comp2フォルダーを作成します。 -
1で作成した
JPX_competitionフォルダーにバックテスト用コードを保存するためのbacktestフォルダーを作成します。 -
SIGNATEのコンペティションサイト よりダウンロードした各種データを2で作成した
data_dir_comp2フォルダーにアップロードします。 -
backtest.pyを こちら からダウンロードし、3で作成したbacktestフォルダにアップロードします。
次にGoogle Colaboratory上でチュートリアルのnotebookを展開します。本チュートリアルのnotebookはGoogle Colaboratory上でも実行可能となっております。各章のnotebookは以下のそれぞれのリンク先を開き、開いたページでRawを右クリックし、「リンク先を名前をつけて保存」を選択することでダウンロード可能です。
以下、3章を例にGoogle Colaboratoryでチュートリアルのnoteboookを使用する方法を説明します。
-
Google Drive の My Drive 内に作成した
JPX_competitionフォルダーに3章用のnotebookを保存するためのChapter03フォルダーを作成します。 -
上記のリンク先から3章のnotebookをダウンロードして、先程作成した
Chapter03フォルダーに20210224_chapter03_tutorial.ipynbというファイル名で保存してください。 -
Google Driveにアップロードした
20210224_chapter03_tutorial.ipynbファイルをダブルクリックして Google Colaboratory で開きます。 -
Google Colaboratoryの環境で本チュートリアルを実行する場合、最初に以下のコードを実行して Google Colaboratory 上の notebook から Google Drive にアクセスできるようにしてください。
# Google Colab環境ではGoogle Driveをマウントしてアクセスできるようにします。
import sys
if 'google.colab' in sys.modules:
# Google Drive をマウントします
from google.colab import drive
mount_dir = "/content/drive"
drive.mount(mount_dir) ここまでの作業を実施した結果、Google DriveのJPX_competitionフォルダーは以下になります。
/content/drive/MyDrive/JPX_competition/
├── Chapter03
│ ├── 20210224_chapter03_tutorial.ipynb
│ └── backtest
│ └── backtest.py
└── data_dir_comp2
├── article.csv.gz
├── disclosureItems.csv.gz
├── industry2.csv.gz
├── industry.csv.gz
├── nikkei_article.csv.gz
├── region.csv.gz
├── stock_fin.csv.gz
├── stock_fin_price.csv.gz
├── stock_labels.csv.gz
├── stock_list.csv.gz
├── stock_price.csv.gz
├── tdnet.csv.gz
└── theme.csv.gz
3.5.3. Dockerをご利用の場合
本チュートリアルのリポジトリを git clone した後、以下の手順を実行していただくことで、Dockerコンテナ内でjupyter notebookを動かすことができます。リポジトリ内の Chapter03 ディレクトリには、本チュートリアルのコードを記載した ipynb(20210224_chapter03_tutorial.ipynb) ファイルを配置しておりますので必要に応じてご活用ください。
Windows環境の場合、コマンド実行には「PowerShell」などをご使用ください。なお、PowerShellの利用に当たっては、最新のセキュリティ事情を踏まえご自身でご判断ください。Dockerのインストールについてはこちらをご参照ください。Dockerの制約としてマウントするパスにはアルファベット、数字、「_」、「.」、「-」以外の文字を使用するとエラーとなることがあるため、パスが前述の文字のみで構成されているディレクトリをご使用ください。
なお、Windows 10 Homeをご利用の場合、Dockerの利用に制限がある場合がありますので、Dockerに習熟した方以外はGoogle Colaboratoryの利用を推奨します。
cd handson/
# 実行するコンテナはsignateユーザーで実行されるため、マウントした領域に書き込めるようにパーミッションを変更します。
chmod -R 777 .
# データ配置先のディレクトリを作成
mkdir data_dir_comp2
# その後作成したhandson/data_dir_comp2に、コンペティションサイトよりデータをダウンロードし配置します。
# Dockerでjupyter notebookを起動します。(初回実行時は約10GBのコンテナイメージをダウンロードします。)
# jupyter notebook作業用に handson ディレクトリを /notebook としてマウントしています。
# jupyter notebook は port 8888でtokenとpasswordを空にして、vscode のjupyter pluginからアクセスできるように xsrf 対策を無効化しています。
docker run --name tutorial --shm-size=2G -v ${PWD}:/notebook -p8888:8888 --rm -it signate/runtime-jpx:2021.03 jupyter notebook --ip 0.0.0.0 --allow-root --no-browser --no-mathjax --NotebookApp.disable_check_xsrf=True --NotebookApp.token='' --NotebookApp.password='' /notebook
# ブラウザで以下のURLにアクセスしてjupyter notebookの画面が表示されていて、本チュートリアル用のnotebookが表示されていることを確認します。
http://localhost:8888/3.6. バックテスト環境の構築
本コンペティション用のバックテスト環境を構築します。金融の世界でバックテストとは一般に価格時系列データを使用して取引をシミュレーションし取引ルールやアルゴリズムなどを評価することを言います。本コンペティションの課題は、モデルにより予測されたポートフォリオのパフォーマンスを競う課題であるため、実際にポートフォリオとして運用した際の期待収益性等について確認・評価することが重要です。また、本コンペティションの評価においても使用しております。実際の評価の具体的な流れは、3.3.5. 評価方法をご参照ください。
バックテストを実施するために最初に必要なことは要件を適切に把握することです。例えば、投資対象となる銘柄群 (ユニバースとも言います)、取引の時間間隔 (数分、数時間、数日)、投資予算の上限、同時に保有可能な銘柄数、1銘柄に投資可能な上限等です。これらを把握しバックテストを実装していくことになります。バックテストの要件を把握することは、モデルを作る際にもモデルの出力要件や評価方法を把握することにもつながります。
評価を公正にするために本コンペティションの評価に用いるものと全く同じロジックが実装されたバックテスト用のコード backtest.py を公開します。このファイルは、こちらからダウンロードしてください。
なお、本チュートリアルではバックテストをスクラッチで実装していますが、アルゴリズムトレーディング用のバックテストライブラリも存在します。有名なライブラリをtips集の「バックテスト用ライブラリ」でご紹介していますのでご参照ください。
3.6.1. 必要なデータ
バックテストの実行には以下のデータが必要になります。
-
ポートフォリオ: バックテスト対象のポートフォリオデータです。(モデルにより予測されたポートフォリオ)
-
stock_price: 株価情報を使用してポートフォリオのリターンを算出します。(stock_price.csv.gz)
-
stock_list: 銘柄リストを使用して予測対象銘柄の情報を取得します。(stock_list.csv.gz)
ポートフォリオは、3.3.4. 提出するモデルの予測出力の定義に記載されているフォーマットのcsvとなります。
3.6.2. 使い方
Backtestモジュールをインポートします。パスが通っていない場合は必要に応じて、sys.pathにBacktestモジュールを配置しているディレクトリを追加してからimportします。
# 以下はパスを通すためのコードになりますので、必要に応じてアンコメントして実行してください。
# import sys
# module_dir = "Backtestモジュールを配置したディレクトリへのフルパス"
# sys.path.append(module_dir)
from backtest import Backtestバックテストを実行するための事前準備として、バックテストに必要なデータを読み込みます。
data_dir = "/notebook/data_dir_comp2" # "左記パスは例です。各自データを配置してるディレクトリへのパスへ変更してください"
# バックテストに必要なデータを取得します。
backtest_codes, backtest_price = Backtest.prepare_data(data_dir)バックテストを実行したいポートフォリオデータを読み込みます。
portofolio_file_path = "SUBMIT.csv" # 左記パスは例です。各自モデルにより予測されたポートフォリオデータが格納されているパスへ変更してください。
df_submit = Backtest.load_submit(portofolio_file_path)バックテストを実行します。
df_results, df_stocks = Backtest.run(df_submit, backtest_codes, backtest_price)「Backtest.run」メソッドの説明
バックテストの実行用メソッドである Backtest.run() への入力データは以下になります。
第一引数: ポートフォリオ (DataFrame)
第二引数: ユニバース (銘柄コード) (List)
第三引数: 株価情報 (DataFrame)バックテストの返り値は以下になります。
df_results: バックテスト結果のサマリー (DataFrame)
df_stocks: 個別銘柄の購入数や日々の価格情報 (DataFrame)3.6.3. 結果の見方
バックテストを実行するとバックテスト結果のサマリーが格納された df_results と、購入数および日々の価格情報が格納された df_stocks の2つのDataFrameが返されます。それぞれのDataFrameの項目は以下の通りです。
df_results の項目は以下の通りです。
bought: 購入金額
cash: 現金
date: 対象週の開始日
day_1: ポートフォリオの月曜日終値での基準価格 (現金含む)
day_2: ポートフォリオの火曜日終値での基準価格 (現金含む)
day_3: ポートフォリオの水曜日終値での基準価格 (現金含む)
day_4: ポートフォリオの木曜日終値での基準価格 (現金含む)
day_5: ポートフォリオの金曜日終値での基準価格 (現金含む)
day_1_return: 月曜日のリターン (%)
day_2_return: 火曜日のリターン (%)
day_3_return: 水曜日のリターン (%)
day_4_return: 木曜日のリターン (%)
day_5_return: 金曜日のリターン (%)
day_1_pl: 月曜日の損益
day_2_pl: 火曜日の損益
day_3_pl: 水曜日の損益
day_4_pl: 木曜日の損益
day_5_pl: 金曜日の損益
exp: 日次リターンの平均
holiday: 祝日の曜日 (0: 月曜日, 4: 金曜日)
sharp: 日次リターンのシャープレシオ
std: 日次リターンの標準偏差
week_pl: 週の損益
week_return: 週のリターン df_stocks の項目は以下の通りです。
actual: 実際に購入した数量
date: 基準日付 (月曜日日付)
Local Code: 銘柄コード
budget: 指定した購入金額
n: 購入順
entry: 週の始値
day_1: 月曜日の終値
day_2: 火曜日の終値
day_3: 水曜日の終値
day_4: 木曜日の終値
day_5: 金曜日の終値
bought: 購入金額
actual: 購入株数3.6.4. バックテストの評価軸と取引戦略
バックテストを実行するとトレードの履歴を得ることができます。それらのトレード履歴を分析して評価してみましょう。トレードの代表的な評価軸としては、以下のようなものがあります。
| 評価軸 | 説明 |
|---|---|
勝率 |
トレードがどの程度勝つかを示す指標です。勝ちトレード数 (利益が0を超えるトレード数) を総トレード数で割ることで算出します。 |
平均リターン |
トレード1回あたりの平均の利益率を示します。合計損益を総トレード数で割ることで算出します。 |
最大ドローダウン |
累積リターンの最大地点からの下落率のことです。取引戦略のリスクを知る上で重要な指標です。 |
ベータ |
ベンチマークとなる指数や取引対象のユニバースに対する合計収益の連動率です。たとえば、ベンチマークとなる指数が10%上昇したときに11%上昇したらベータは1.1となります。 |
ペイオフレシオ |
トレード1回あたりの損益率を示します。トレードの平均利益を平均損失で割ることで算出します。 |
シャープレシオ |
リスクに応じた利益を得られているかを示します。リターンから安全資産利回りを引いてそのリターンの標準偏差で割ることで算出します。週・月・年などの計算の単位で大きく結果が変わることに注意が必要です。日本株のアルゴリズムトレードの評価では、安定資産利回りは0%で計算することが多いです。 |
インフォメーション・レシオ |
ベンチマークと比べて安定した利益を得られているかを示します。リターンからベンチマーク利回りを引いたものを平均して標準偏差で割ることで算出します。 |
バックテスト実行時は、一つの評価軸のみを確認するのではなく、複数の評価軸を組み合わせて解釈することでトレード戦略の特性を把握することが重要です。考慮すべき観点は多数存在しますが、その一部を紹介します。
-
勝率のみに注目すると、小さい勝ちを積み重ねていても、実際には大きな負けにより収益を失っていることに気づかないことがあります。そのため、平均リターンやペイオフレシオとセットで確認し、高い勝率を実現するために何をトレードオフにしているかに注目しましょう。
-
取引戦略はマーケット全体の動きの影響を強く受けます。その取引戦略のユニバースに対する特性を知るために、まずはベータを確認しましょう。一般的にベータが高い取引戦略を取っている場合、マーケット全体の暴落時に大きな暴落が発生することになるため、ベータが高い取引戦略では最大ドローダウンが大きくなる傾向があることに注意が必要です。逆に低いベータで同等の収益性が実現できている取引戦略は、高いベータの取引戦略よりも相対的にリスクが低く、パフォーマンスが安定すると考えることができます。
-
最大ドローダウンは、その取引戦略のリスクを評価する上で重要な評価軸です。自分の取引戦略が過去に最大でどのくらいの下落をしたかは常に把握しましょう。
-
取引戦略の評価をする際に対比軸となるベンチマークをどのように設定するかを常に考えましょう。本チュートリアルでは、取引戦略の効果を評価するため取引可能な全銘柄の平均リターンをベンチマークに採用しています。本コンペティションではデータは提供されていませんが、TOPIXや日経平均株価等もベンチマークとして採用されることが多く、それぞれ特性が異なります。
-
取引戦略を評価する際は、バックテストを行う期間におけるマーケットの特性を把握することが重要です。例えば、2020年は新型コロナウイルス感染症(COVID‑19)の影響で、前半マーケットは大きく値下がりした後、世界的に経済対策のための金融緩和が加速し結果的に歴史的な株高となりました。このような期間でも安定的に勝てる取引戦略は、前半の暴落に対する備えと、後半のトレンドが発生した時に収益化できる特性を両方備えている必要があります。2016年から2019年においてもそれぞれマーケットの特性がありますので、取引戦略の評価をする際はできるだけ多角的に多用な期間を評価し、その取引戦略の強み・弱みをしっかりと把握することが重要です。
-
取引戦略を評価する上で重要となるのが実現可能性です。今回は取引コストを0と仮定しているため、細かくポートフォリオを入れ替えることにパフォーマンスのペナルティは発生しませんが、実際に取引を行う場合は取引手数料は重要な要素となります。また、本コンペの評価手法に関連する箇所としては、取引対象として指定した数量を市場の始値で本当に購入できるか、というポイントもあります。本コンペでは取引対象のユニバースを時価総額200億円以上としているため、個人で取引を行う上でも流動性等についてそこまで大きな問題にはなりませんが、より時価総額が小型の株式銘柄をユニバースとして利用する場合はこの観点も注意してください。
-
平均リターンや勝率などを株価の動きそのものではなく、取引対象銘柄の平均をベンチマークとして、ベンチマークとの相対的な差を計算することで相対的なリターン(残差リターンなどと呼ばれます)や相対的な勝率を計算することができます。例えば、ベンチマークが10%下落したときに、ポートフォリオが1%の下落に収まっている場合、相対的なリターンは+9%勝っていることになります。このようなベンチマーク対比の計算も合わせて行うことで、より多角的な評価をすることが可能になります。
3.7. シンプルなポートフォリオ組成モデルの作成
バックテストの実行方法を理解したので、いよいよシンプルなポートフォリオ組成モデルを作成しましょう。ポートフォリオ組成モデルを作成することを通して、本コンペティションに投稿するモデルの出力や評価方法を把握し、最終的には作成したモデルを投稿して結果がリーダーボードに掲載されることを確認します。
本節では以下を説明しています。
-
ポートフォリオ組成モデルの作成方法
-
バックテストの使用方法
-
投稿用パッケージの作成方法
具体的には、以下のステップで進めていきます。
1. 必要なライブラリの読み込み
2. データセットの読み込み
3. ポートフォリオ組成戦略の策定
4. ポートフォリオの組成
5. 出力の調整
6. バックテストの実行
7. バックテストの評価
8. 投稿用パッケージのディレクトリ作成
9. 作成したコードをランタイム実行用にクラスにまとめる
10. 提出用パッケージの作成と提出3.7.1. 必要な入力データ等
■バックテスト用クラス
本コンペティションの評価方法と同等のロジックを実装したバックテスト用のクラスを提供しています。本notebookからimportできる必要があります。import時にエラーとなる場合は、`backtest.py` ファイルをダウンロードしている確認の上、sys.path に追加して再実行してください。なお、バックテスト用のクラスの取得方法は、「3.6. バックテスト環境の構築」をご参照ください。
■データセット
本章で構築するモデルにおいては、以下のデータファイルを使用します。そのため、コンペティションサイトからダウンロードしたデータファイルを配置し、ディレクトリパスを dataset_dir 変数に設定してください。
-
stock_list.csv.gz
-
stock_price.csv.gz
3.7.2. 必要なライブラリの読み込み
ランタイム環境とGoogle Colaboratory環境の両者で共通のライブラリを使用するためにバージョンを調整します。
!pip install --no-cache-dir joblib==1.0.1 numpy==1.19.5 pandas==1.1.5 scikit-learn==0.20.3 scipy==1.2.1 seaborn==0.9.0以下のライブラリを読み込みます。
import io
import os
import sys
import zipfile
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from tqdm.auto import tqdm
from scipy import stats
from IPython.core.magic import register_cell_magic次に本コンペティションの評価検証用のバックテストモジュールを読み込みます。インポート時にエラーが出た場合は、sys.path に backtest.py ファイルを配置したディレクトリを追加してから再度インポートしてください。
# インポート時にエラーが出た場合は、以下のmodule_dirをbacktest.pyを配置したディレクトリに変更してください。
import sys
if 'google.colab' in sys.modules:
# Backtestを配置したディレクトリへのフルパスを指定します
module_dir = f"{mount_dir}/MyDrive/JPX_competition/Chapter03/backtest"
else:
# Backtestを配置したディレクトリへのフルパスを指定します
module_dir = "/notebook/Chapter03/backtest"
sys.path.append(module_dir)
from backtest import BacktestPandasのデータを表示する際に表略されないように設定を変更します。
# 表示用の設定を変更します
pd.options.display.max_rows = 100
pd.options.display.max_columns = 100
pd.options.display.width = 1203.7.3. データセットの読み込み
データセットを配置したディレクトリのパスを設定します。Google Colabをご利用の場合は Google Drive にデータセットをアップロードして、そのディレクトリを指定してください。また、データセットの取得方法および内容については「3.4. データセットの説明」をご参照ください。
# データセットを配置したディレクトリのパスを設定
if 'google.colab' in sys.modules:
dataset_dir = f"{mount_dir}/MyDrive/JPX_competition/data_dir_comp2"
else:
dataset_dir = "/notebook/data_dir_comp2" 本コンペティションのランタイム環境におけるデータセットへのアクセスは、 ScoringService.predict() メソッドに渡されるinputsパラメーターを通して行う必要があります。そのため、以下のように本notebook環境でもランタイム環境と共通の方法でデータセットにアクセスすることで、コードが複雑になったり投稿用にコードを編集したりしなくても済むようにしています。
# 入力パラメーターを設定します。ランタイム環境での実行時と同一フォーマットにします
inputs = {
"stock_list": f"{dataset_dir}/stock_list.csv.gz",
"stock_price": f"{dataset_dir}/stock_price.csv.gz",
}本コンペティションでは2016年以降のデータを提供していますが、本notebookではモデル作成・評価時の処理時間を短くするために 2020-01-01 以降のデータを使用してバックテストを実施・評価します。なお、実際に評価をする場合は可能な限り長い期間を評価に利用することを推奨します。
# 投資対象日付を指定します
start_dt = pd.Timestamp("2020-01-01") ランタイム環境においては ScoringService.predict() メソッドに渡されるinputsパラメーターに purchase_date というキー名で予測対象日が記載されたCSV形式のファイルへのパスが渡され、そのファイル内に記載されている日付を予測対象日として使用します。ここではランタイム環境に対応するために purchase_date が存在する場合は、指定された日付を使用するロジックを組み込んでおきます。purchase_date のフォーマットについては SIGNATEのコンペティションサイト にサンプルファイルが配置されているためそちらをご参照ください。
if "purchase_date" in inputs.keys():
# ランタイム環境では指定された投資対象日付を使用します
# purchase_dateを読み込み
df_purchase_date = pd.read_csv(inputs["purchase_date"])
# purchase_dateの最も古い日付を投資対象日付として使用します
start_dt = pd.Timestamp(df_purchase_date.sort_values("Purchase Date").iloc[0, 0])本コンペティションでは投資対象となる銘柄群 (ユニバース) が設定されています。そのため、ユニバース内の銘柄に絞って処理を実施するために銘柄情報を読み込みます。
# 銘柄情報読み込み
df_stock_list = pd.read_csv(inputs["stock_list"])
# 問題2のユニバース (投資対象の条件を満たす銘柄群) 取得
codes = df_stock_list.loc[
df_stock_list.loc[:, "universe_comp2"] == True, "Local Code"
].unique()以下では、シンプルに株価情報のみを利用してポートフォリオを組成するために株価情報を読み込んでいます。本コンペティションでは、データセットはcsv.gz形式で提供していますので、データの型情報が保存されていません。そのため、特に日付型のカラムについては明示的に変換する必要があります。read_csvのparse_dateパラメーター等、日付型を指定する方法は複数ありますが、本notebookでは一度読み込んでから変換しています。
# 価格情報読み込み、インデックス作成
df_price = pd.read_csv(inputs["stock_price"]).set_index("EndOfDayQuote Date")
# 日付型に変換
df_price.index = pd.to_datetime(df_price.index, format="%Y-%m-%d")処理時間を最適化するために処理対象データを日付でフィルタをして絞り込みます。本notebookでは過去20営業日のデータを使用して特徴量を作成するため、投資対象日付から過去20営業日時点のデータを含める必要がありますが、バッファとして過去30日のデータを含めることにします。同時に株価情報をユニバースと一致するように絞り込んでいます。
# 投資対象日の前週金曜日時点で予測を出力するため、予測出力用の日付を設定します。
pred_start_dt = pd.Timestamp(start_dt) - pd.Timedelta("3D")
# 特徴量の生成に必要な日数をバッファとして設定
n = 30
# データ絞り込み日付設定
data_start_dt = pred_start_dt - pd.offsets.BDay(n)
# 日付で絞り込み
filter_date = df_price.index >= data_start_dt
# 銘柄をユニバースで絞り込み
filter_universe = df_price.loc[:, "Local Code"].isin(codes)
# 絞り込み実施
df_price = df_price.loc[filter_date & filter_universe] head() や tail() メソッドを使用して処理結果が期待通りとなっていることを確認しながら進めていきます。ここではデータが2019年11月20日以降に絞り込まれていることが確認できます。`.T` プロパティ https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.transpose.html#pandas.DataFrame.transpose を使用して行と列を入れ替えることで可読性が上がる場合があります。
ここで計算したデータセットのフォーマットを確認するために、データセットの先頭を見てみます。
df_price.head(3).T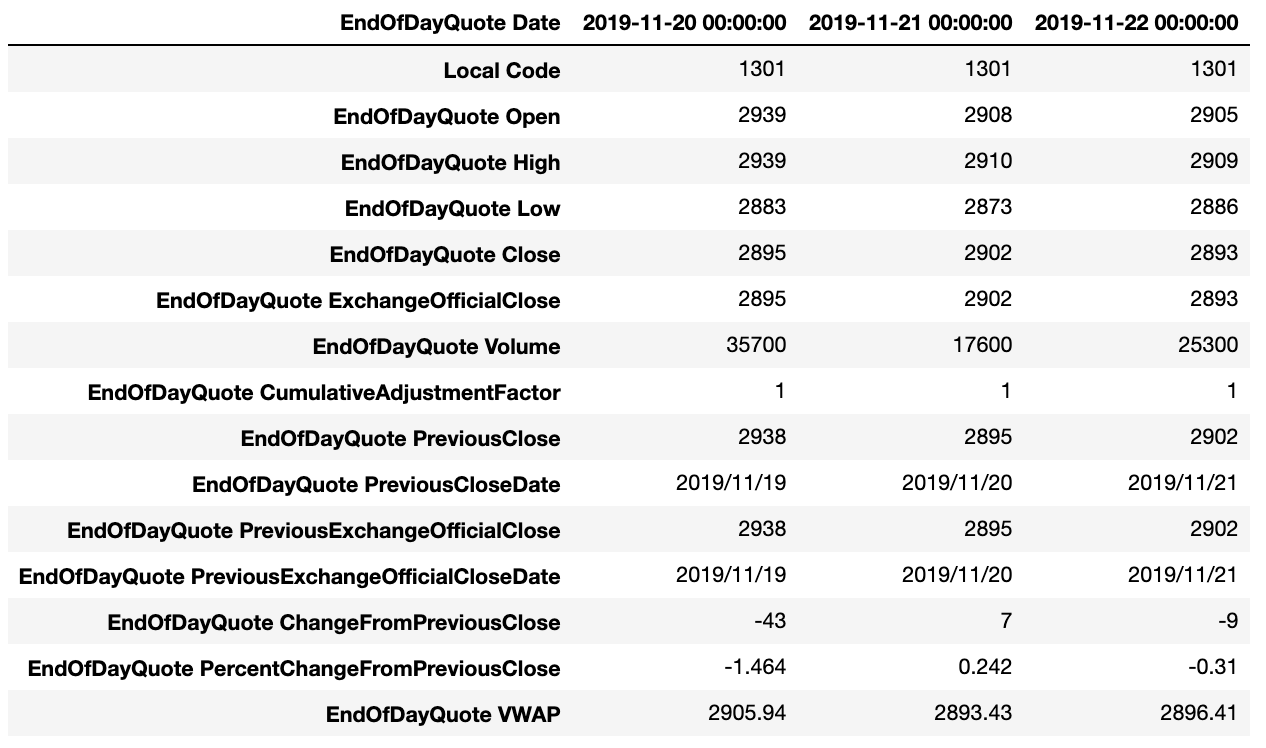
3.7.4. ポートフォリオ構築戦略の策定
ポートフォリオを組成するための特徴量を作成します。今回は以下の2種類の戦略を採用します。
-
リターン・リバーサル (逆張り) 戦略を採用して、過去1ヶ月(約20営業日)の株価下落率の上位25銘柄を選択します。 (「リターン・リバーサル」 野村證券証券用語解説集より引用 https://www.nomura.co.jp/terms/japan/ri/A01944.html)
-
トレンドフォロー (順張り) 戦略を採用して、過去1ヶ月(約20営業日)の株価上昇率の上位25銘柄を選択します。 (「トレンドフォロー」 野村證券証券用語解説集より引用 https://www.nomura.co.jp/terms/japan/ta/A02002.html)
過去1ヶ月(20営業日)の株価下落率/上昇率を計算するために、銘柄毎にグループ化してから株価変化率を計算します。
本コンペティションに提出するポートフォリオは各週の週初の営業日に買付実施されるため、買付日前週の金曜日終値時点を銘柄選択の基準とします。基準日のデータを取得するために単純に金曜日にのみ絞り込んだ場合、金曜日が祝日の場合にその翌週の銘柄を選択できなくなるおそれがあるため、平日でリサンプル(pandasにおいて平日を意味する B を指定してresample関数を呼んでいます)し、欠損値がある場合には前日の値を使うように前方補完(pandasではffill関数を利用)を実施します。これにより、金曜日に必ずデータが存在するようにしています。
# 欠損値がある場合にも正しく動作しているかを確認するため、処理前に木曜日、金曜日が祝日である2020-07-23、2020-07-24のレコードが存在しないことを確認しておきます。
df_price.loc["2020-07-22":"2020-07-27"].head(4)
# groupby を使用して処理するために並び替え
df_price.sort_values(["Local Code", "EndOfDayQuote Date"], inplace=True)
# 銘柄毎にグループにします。
grouped_price = df_price.groupby("Local Code")[
"EndOfDayQuote ExchangeOfficialClose"
]
# 銘柄毎に20営業日の変化率を作成してから、金曜日に必ずデータが存在するようにリサンプルして前方補完します。
df_feature = grouped_price.apply(
lambda x: x.pct_change(20).resample("B").ffill().dropna()
).to_frame()大量のデータを処理する場合、処理によっては数分から数時間かかる場合があります。処理済みのデータを保存しておくことで、処理時間のかかる処理を省略して作業できるようにすることは重要なテクニックの一つです。今回はメモリ上に別の変数として保存しておきますが、セッションが閉じられる際に処理済みデータもクリアされてしまうことに加えて、大量のデータである場合はメモリ上に保存しておくとメモリを圧迫するため、ファイルに書き出しておいて必要な時にファイルから読み込むのが良い方法です。
Pandasには様々な形式でのデータの入出力用メソッド (リンク) が用意されています。例えば、データが圧縮されて型が保存される to_hdf メソッド (リンク)を使用してファイルに書き出し、対応する read_hdf メソッド (リンク)で読み出すことで簡単にデータフレームを読み書きできます。
平日を指定してデータのリサンプル行い、欠損値に前日の値を使うように前方補完した結果が期待通りになっているかを確認しましょう。2020-07-23及び2020-07-24はそれぞれ木曜日及び金曜日の祝日でしたので、2020-07-23及び2020-07-24に2020-07-22の値が入っていれば良いことになります。
# 上記は比較的時間のかかる処理なので、処理済みデータを別に残しておきます。
df_work = df_feature.copy()
# 処理後に木曜日、金曜日が祝日である2020-07-23、2020-07-24のレコードが前方補完されていることを確認します。
df_work.loc[(slice(None), slice("2020-07-22", "2020-07-27")),].head(4)下図のように木曜及び金曜の祝日である2020-07-23及び2020-07-24に2020-07-22の値が入っていることが確認できます。
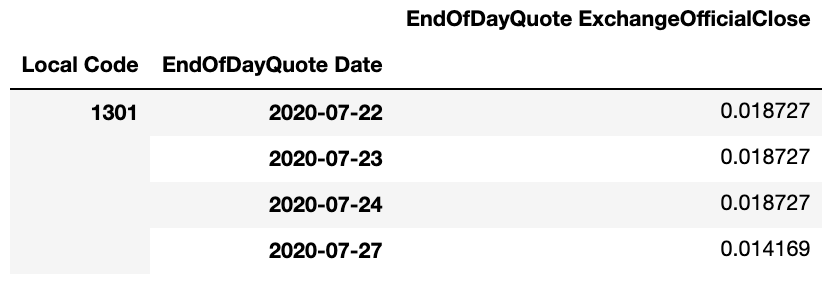
以下のコードでデータを整えます。インデックスとカラム名を調整しています。
# インデックスが銘柄コードと日付になっているため、日付のみに変更します。
df_work = df_work.reset_index(level=[0])
# カラム名を変更します。
df_work.rename(
columns={"EndOfDayQuote ExchangeOfficialClose": "pct_change"},
inplace=True,
)
# データをpred_start_dt以降の日付に絞り込みます。
df_work = df_work.loc[df_work.index >= pred_start_dt]特徴量が生成されていることを確認します。
# df_workの最初の3行を出力する。
df_work.head(3)
3.7.5. ポートフォリオ組成を行う上での注意事項
本コンペのようにデータサイエンス的な手法で取引戦略を構築する上で重要なのは、取引戦略に合致した銘柄選択を実施してポートフォリオを組成することです。取引戦略をデータサイエンスな的手法で構築している場合、そこから実現したい収益は、統計的に他の銘柄よりも収益性が高い銘柄をモデルが選択することで達成しているはずです。しかし、実際に良いモデルを作ることができても、そこから収益を実現するためには工夫が必要となります。ここでは、その際の注意点を考察します。
取引対象銘柄数の選択
予測モデルのスコアから収益を実現するためには、ポートフォリオを組成する取引対象銘柄の数の選択が重要となります。予測モデルから算出されるスコアが高い収益を仮に予測できていたとしても、取引対象銘柄の数が少なすぎると決算などの銘柄の個々の要因により予測した収益性の効果が消されることがあります。
同一の合計金額で株式を購入する際、スコアの上位5銘柄で組成したポートフォリオと上位20銘柄で組成したポートフォリオのどちらのポートフォリオが、銘柄の個々の要因の影響を受けにくいかを考えると、20銘柄の方が影響を受けにくいことになります。ただし、取引銘柄数を増やしすぎると取引戦略の実現に必要な現金が増えたり、スコアの有効性があまり無い銘柄もポートフォリオに含まれる可能性があるため、最終的な購入銘柄数はバックテストを通して調整する必要があります。
なお、データサイエンス的手法の利用用途において、まれに発生する現象を探索するような方法(アノマリーディテクションなどと呼ばれます)があります。このようなモデルでは20銘柄も有効なスコアが出ていない可能性があります。この場合、バックテストを通して、有効性が高いスコアのしきい値を探索し、ある一定のスコアを超えていたら売買を行うようなロジックを構築することもあります。
購入金額の決定
購入金額は特別な理由が無い限りは、銘柄ごとにある程度均等になるように購入するのが良いでしょう。直感的には予測スコアの上位の銘柄を、より多く購入したいと考えるかもしれませんが、この試みは結果的に予測スコアの上位の銘柄の個々の要因により負ける可能性を増やすことに繋がります。予測モデルで収益性を予測してみると、そのスコアの統計的な効果はさほど強くない(未来の値動きに対する相関係数は0.1から高くても0.2程度に収まる)ことが多く、上位のスコアの銘柄に対して取引金額の割合をより多くするほどの統計的な強度は観測されていないことが多いです。
また、最上位の予測スコアの銘柄には注意が必要です。データサイエンス的な手法でモデルを作ると、外れ値等に反応するモデルが出来上がることがあります。このような動きは、例えば特別損失の適時開示等のコーポレーションアクションで引き起こされている事が多く、リスク回避の観点からはそのようなモデルは取引対象に含めるべきではありません。本コンペティションのデータには、TDnetのデータが含まれているため、そのような銘柄を予め取引対象のユニバースから除外するアプローチも後ほど紹介しています。
3.7.6. ポートフォリオの組成手順
今回のポートフォリオでは買付日前週の金曜日終値時点を銘柄選択の基準とするため、金曜日のデータのみに絞り込みます。すでに「3.7.4. ポートフォリオ構築戦略の策定」において、金曜日が祝日の場合の処理はしていますので、そのまま金曜日に絞り込んで問題ありません。
# 金曜日のデータのみに絞り込みます
df_work = df_work.loc[df_work.index.dayofweek == 4]金曜日のデータのみとなっていることを確認します
# df_workの最初の2行を出力する。
df_work.head(2)
次に、日付毎にグループ化してから、下落率上位25銘柄を選択しています。本コンペティションの評価では、出力されたポートフォリオに記載されている順番で銘柄が購入されるため、なるべくリターンが高くなる銘柄から先に出力して購入されるようにすることが最適と考えられます。ここでは、下落率が高い銘柄ほどリターンの大きくなるとの仮説を立てて、`pct_change` について昇順で並べ替えてから銘柄を選択しています。こうすることで下落率が高い銘柄順に出力されるようにしています。
なお、ここでは説明をシンプルにするために特に理由なく25銘柄を選択していますが、例えば、5銘柄から50銘柄まで5銘柄ずつ増加させた合計10個のポートフォリオを組成してバックテストでパフォーマンスを比較することで、この戦略における最適な選択銘柄数を見つけられるかもしれません。また、その場合、50銘柄のポートフォリオを組成しておいて、バックテスト投入時に銘柄数を絞り込むロジックを組むことで処理時間を最適化できるかもしれません。
# 日付毎に処理するためグループ化します
grouped_work = df_work.groupby("EndOfDayQuote Date", as_index=False)# 選択する銘柄数を指定します
number_of_portfolio_stocks = 25
# ポートフォリオの組成方法を戦略に応じて調整します
strategies = {
# リターン・リバーサル戦略
"reversal": {"asc": True},
# トレンドフォロー戦略
"trend": {"asc": False},
}
# 戦略に応じたポートフォリオを保存します
df_portfolios = {}
# strategy_id が設定されていない場合は全ての戦略のポートフォリオを作成します
if "strategy_id" not in locals():
strategy_id = None
for i in [strategy_id] if strategy_id is not None else strategies.keys():
# 日付毎に戦略に応じた上位25銘柄を選択します。
df_portfolios[i] = grouped_work.apply(
lambda x: x.sort_values(
"pct_change", ascending=strategies[i]["asc"]
).head(number_of_portfolio_stocks)
)以下を確認します。
-
1つの週に対して25銘柄選択されていること
-
戦略に応じてpct_changeの値が反転していること
# 結果結合用
buff = []
# 戦略毎に処理
for i in df_portfolios.keys():
# ポートフォリオを表示用に保存
buff.append(
df_portfolios[i]
# マルチインデックスは操作しにくいので日付のみに変更します
.reset_index(level=[0])
# 先頭の26レコードを取得します
.head(26)
# 結合した後の列名をわかりやすくするために変更します
.rename(columns={v: f"{i}_" + v for v in df_portfolios[i].columns})
)
# 結合して保存
pd.concat(buff, axis=1)
ポートフォリオに組み入れる銘柄を決めたので、各銘柄について購入金額を指定します。今回はシンプルにするために50,000円を一律で指定して購入金額の総額を25銘柄分で合計125万とすることで、1株の価格が5万円を超えている銘柄が含まれていても予算上限に近い金額を購入できるようにしています。株価を参照して銘柄数や購入金額を調整することも検討してみてください。なお、本コンペティションのポートフォリオは、対象週の月曜日日付を指定する必要がありますので、金曜日から月曜日日付に変更しています。
# 銘柄ごとの購入金額を指定
budget = 50000
# 戦略毎に処理
for i in df_portfolios.keys():
# 購入株式数を設定
df_portfolios[i].loc[:, "budget"] = budget
# インデックスを日付のみにします
df_portfolios[i].reset_index(level=[0], inplace=True)
# 金曜日から月曜日日付に変更
df_portfolios[i].index = df_portfolios[i].index + pd.Timedelta("3D")これでポートフォリオが完成しました。完成したデータを確認します。
# 戦略毎に処理
for i in df_portfolios.keys():
# 戦略名を表示
display(i)
# 表示
display(df_portfolios[i].head(3))
ポートフォリオ組成に用いた特徴量やその他のカラムが残っているため、本コンペティションで決められている出力フォーマットと一致するように出力を調整します。
3.7.7. 出力の調整
本コンペティションのポートフォリオの出力フォーマットは「3.3.4. 提出するモデルの予測出力の定義」をご参照ください。ここでは出力フォーマットに合わせるためにインデックス名やカラム数を調整します。
# 戦略毎に処理
for i in df_portfolios.keys():
# インデックス名を設定
df_portfolios[i].index.name = "date"
# 出力するカラムを絞り込みます
df_portfolios[i] = df_portfolios[i].loc[:, ["Local Code", "budget"]]ポートフォリオが出力フォーマットと一致していることを確認します。
# 戦略毎に処理
for i in df_portfolios.keys():
# ポートフォリオを確認
display(df_portfolios[i].head(3))
本コンペティションの ScoringService.predict の出力仕様はcsv形式の文字列であるため、仕様に合わせて出力します。
# 出力保存用
outputs = {}
# 戦略毎に処理
for i in df_portfolios.keys():
# 出力します
out = io.StringIO()
# CSV形式で出力
df_portfolios[i].to_csv(out, header=True)
# 出力を保存
outputs[i] = out.getvalue()出力を確認します。
# 戦略毎に処理
for i in outputs.keys():
# 戦略名を表示
print(f'// "{i}"')
# 出力を確認
print("\n".join(outputs[i].split("\n")[:4]))出力
// "reversal"
date,Local Code,budget
2020-01-06,4592,50000
2020-01-06,3254,50000
2020-01-06,6875,50000
// "trend"
date,Local Code,budget
2020-01-06,6387,50000
2020-01-06,4772,50000
2020-01-06,6195,50000バックテスト用に出力を保存しておきます。
# 戦略毎に処理
for i in outputs.keys():
# 出力を保存します。
with open(f"chapter03-tutorial-01-{i}.csv", mode="w") as f:
# ポートフォリオをファイルに書き出します。
f.write(outputs[i])3.7.8. バックテストの実行
本コンペティションの Public LB および Private LB と同等の評価ロジックを実装したバックテスト用の backtest.py ファイルを使用して、作成したポートフォリオを評価します。
バックテストの使用法などの詳細は、「3.6. バックテスト環境の構築」をご参照ください。
初めにバックテストを使用する際に必要なデータを準備します。バックテストの実行には以下の3つのデータが必要になります。
-
ユニバース (stock_list.csv.gz)
-
株価 (stock_price.csv.gz)
-
テスト対象のポートフォリオ
Backtest.prepare_data に1および2のデータを保存しているディレクトリへのパスを指定して、必要なデータをロードします。
# データを保存しているディレクトリを指定します。
backtest_dataset_dir = dataset_dir
# バックテストに必要なデータを読み込みます。
backtest_codes, backtest_price = Backtest.prepare_data(backtest_dataset_dir)バックテスト対象の戦略であるリターン・リバーサル戦略とトレンドフォロー戦略を定義します。
# ポートフォリオの組成方法
backtest_strategies = {
# リターン・リバーサル戦略
"reversal": {},
# トレンドフォロー戦略
"trend": {},
} Backtest.load_submit にテスト対象のポートフォリオを保存したファイルへのパスを指定して読み込みます。`load_submit` ではデータを読み込み時にフォーマットのチェックをしたり、レコード順を付与するなどのバックテスト実行のための前処理を実施しています。
# ポートフォリオデータ保存用
df_submits = {}
# 先ほど出力したポートフィリオデータを読み込みます
for i in backtest_strategies.keys():
# ポートフォリオを読み込み
df_submits[i] = Backtest.load_submit(f"chapter03-tutorial-01-{i}.csv")3つのデータを指定してバックテストを実行します。
# バックテスト結果リターン情報保存用
results = {}
# バックテスト結果銘柄情報保存用
stocks = {}
# 戦略毎に処理
for i in tqdm(backtest_strategies.keys()):
# バックテストを実行します
results[i], stocks[i] = Backtest.run(df_submits[i], backtest_codes, backtest_price)
返り値を確認します。評価は下記で実施します。
# バックテスト結果のサマリー
results["reversal"].head(3)
# 銘柄毎の情報
stocks["reversal"].head(3)
3.7.9. バックテストの評価
バックテストを実行して取得した、週毎のリターン情報と各銘柄毎の購入結果数の情報を評価していきます。各評価項目の定義については、「3.6.4. バックテストの評価軸と取引戦略」をご参照ください。
結果の評価として以下を実施します。
週毎のリターンデータ
-
週毎の運用実績(PL)の分布をプロット (週毎の運用実績の合計値が本コンペティションの評価項目)
-
週毎の運用実績の統計量の算出
-
週毎の勝率・ペイオフレシオ・シャープレシオの算出
-
週毎のリターン推移のプロット
-
曜日別分析のためのバイオリンプロット
-
週毎のリターンの累積プロット
-
ユニバースとの散布図
-
ユニバースに対するベータを計算
1.週毎の運用実績の分布をプロット
まず、週毎の運用実績の分布をプロットしてみます。
# 描画領域を定義
fig, axes = plt.subplots(1, len(results), figsize=(8 * len(results), 8), sharex=True, sharey=True)
# 戦略毎に処理
for i, k in enumerate(results.keys()):
# 描画位置を指定
ax = axes[i]
# 分布をプロット
results[k].week_pl.hist(bins=25, ax=ax)
# タイトルを設定
ax.set_title(f"{k}: week pl distribution")
# 描画
plt.show()
trendとreversalは共にほぼ0平均に見えますが、reversalは分布が若干広いように見え、週によっては大きなマイナスも観測されていることがわかります。おそらくCOVID-19の暴落が発生した週が該当すると想像できます。ただし、大きなプラスの週もあるため、その負けを取り返しているかもしれません。ただ、このプロットだけではあまり戦略の良し悪しはわかりません。
2.週毎の運用実績の統計量を算出
週毎の運用実績の統計量を算出します。
# week_plの分布の統計量
# 結合用データ保存
buff = []
# ストラテジー毎に処理
for k in results.keys():
# week_plの統計量を取得します。
df = results[k].loc[:, ["week_pl"]].describe().T
# インデックスを編集してストラテジーのIDにする
df.index = [k]
# インデックス名変更
df.index.name = "strategy_id"
# 結合用に保存
buff.append(df)
# 結合して表示
pd.concat(buff)
週毎の運用実績の統計量を確認すると、reversalがtrendより平均(mean)が高いことがわかります。ただし、中央値(50%)を確認するとtrendの方が高いのでreversalは小さな勝ちではなく、大きな勝ちを利用して平均を押し上げていることがわかります。また、25%分位点では大きな差異はないのに最小値はreversalがずっと小さいことから、大きな負けがあると想定されます。
3.週毎の勝率、ペイオフレシオ、シャープレシオを算出
週毎の勝率、ペイオフレシオ、シャープレシオを算出します。
# 結合用データ保存
buff = []
# 戦略毎に処理
for k in results.keys():
df_return = results[k]
# 計算結果保存用
d = {}
# 件数
d["count"] = df_return.shape[0]
# 勝率
d["win_ratio"] = (
df_return.loc[df_return.loc[:, "week_return"] > 0].shape[0] / d["count"]
)
# ペイオフレシオ
d["payoff_ratio"] = df_return.loc[
df_return.loc[:, "week_return"] > 0, "week_return"
].mean() / (
-1 * df_return.loc[df_return.loc[:, "week_return"] <= 0, "week_return"].mean()
)
# シャープレシオ
d["sharp"] = (
df_return.loc[:, "week_return"].mean() / df_return.loc[:, "week_return"].std()
)
# 平均PL
d["avgPL"] = df_return.loc[:, "week_pl"].mean()
# week_plの合計
d["PL"] = df_return.loc[:, "week_pl"].sum()
# strategy_idを設定
df = pd.DataFrame([d], index=[k])
# インデックス名を指定
df.index.name = "strategy_id"
# 結合用に保存
buff.append(df)
# 結合して表示
pd.concat(buff)
reversalの週毎の勝率は50%ですが、payoff_ratioも1がより大きく一回の勝ちが負けよりおおきいことがわかります。trendはを勝率が60%を超えており、reversalよりも安定的に勝てるポートフォリオの可能性があります。
4.週毎に曜日別のリターンをプロット
週毎の1日目から5日目までのリターンの推移をプロットし、曜日毎に勝ち負けの分布に差異が無いかを確認しています。
# 描画領域を定義
fig, axes = plt.subplots(
len(results), 1, figsize=(20, 4 * len(results)), sharex=True, sharey=True
)
# 描画用データ保存用
dfs_plot = {}
# 戦略毎に処理
for i, k in enumerate(results.keys()):
# 描画位置を指定
ax = axes[i]
# 列を行に変換
dfs_plot[k] = (
results[k]
.set_index("date")
.loc[
:,
[
"day_1_return",
"day_2_return",
"day_3_return",
"day_4_return",
"day_5_return",
],
]
.stack()
.to_frame()
.reset_index()
.rename(columns={0: "return"})
)
# 作業用に変数設定
df_plot = dfs_plot[k]
# 曜日毎のreturnをプロット
df_plot.groupby(["level_1", "date"]).first().unstack().plot(ax=ax, legend=False)
# タイトルを設定
ax.set_title(f"{k}: Daily returns")
# リターンが0の位置に基準線を描画
ax.axhline(y=0, color="black")
# グリッドを表示
ax.grid(True)
# 描画
plt.show()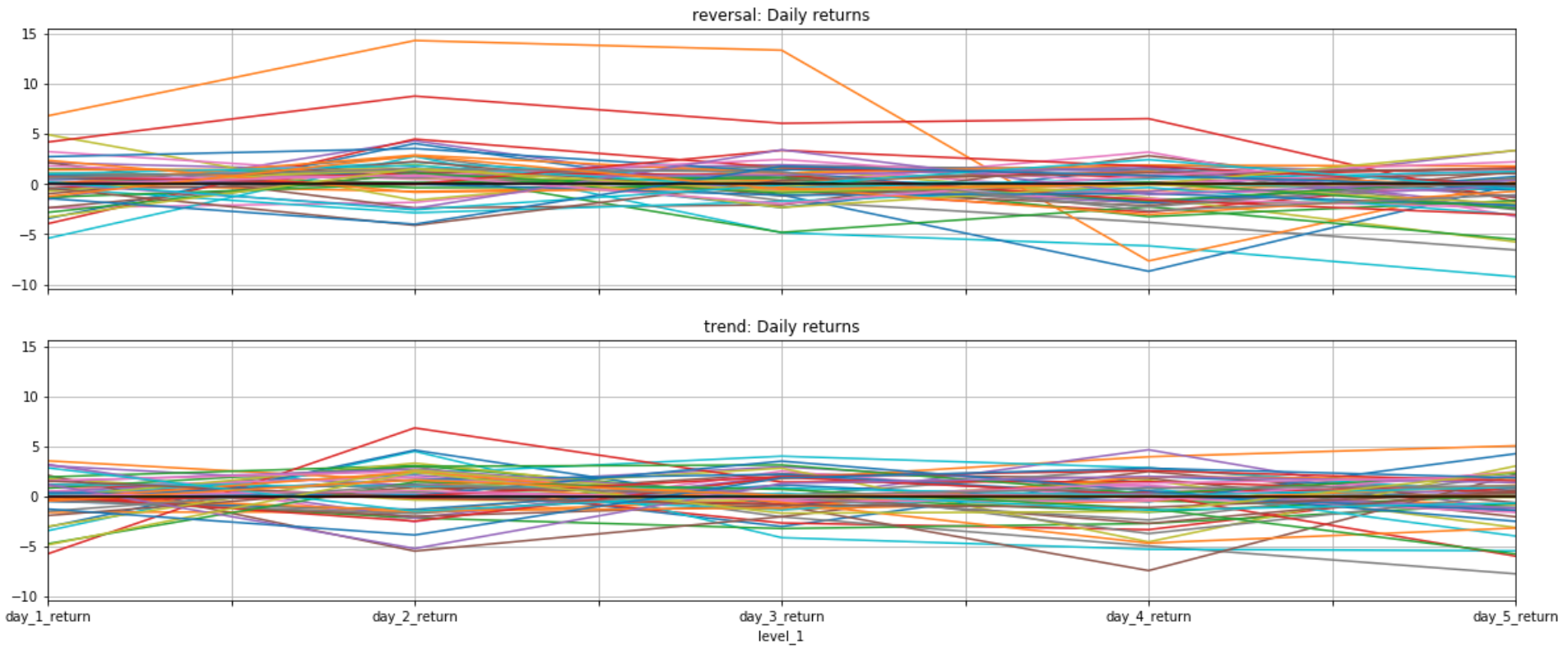
5. 曜日別分析のためのバイオリンプロット
上のグラフでは何が起きているかわかりにくいので、seabornのバイオリンプロット(リンク)を利用します。バイオリンプロットはデータの密度分布を確認できるグラフであり、統計的な差異がありそうな箇所を発見するために便利です。バイオリンの形状はカーネル密度推定による確率密度関数を表しており、バイオリンの中心部分に平均、中央値、25%タイル、75%タイルを示す箱が表示されています。
# 描画領域を定義
fig, axes = plt.subplots(len(results), 1, figsize=(15, 4 * len(results)), sharex=True, sharey=True)
# 戦略毎に処理
for i, k in enumerate(results.keys()):
# 描画位置を指定
ax = axes[i]
# 箱が見やすいように横方向を指定してプロット
sns.violinplot(x="return", y="level_1", data=dfs_plot[k], ax=ax, orient="h")
# タイトルを設定
ax.set_title(f"{k}: daily return")
# グリッドを表示
ax.grid(True)
# 文字が重なって読みにくいので間隔調整
fig.tight_layout(pad=2.0)
# 描画
plt.show()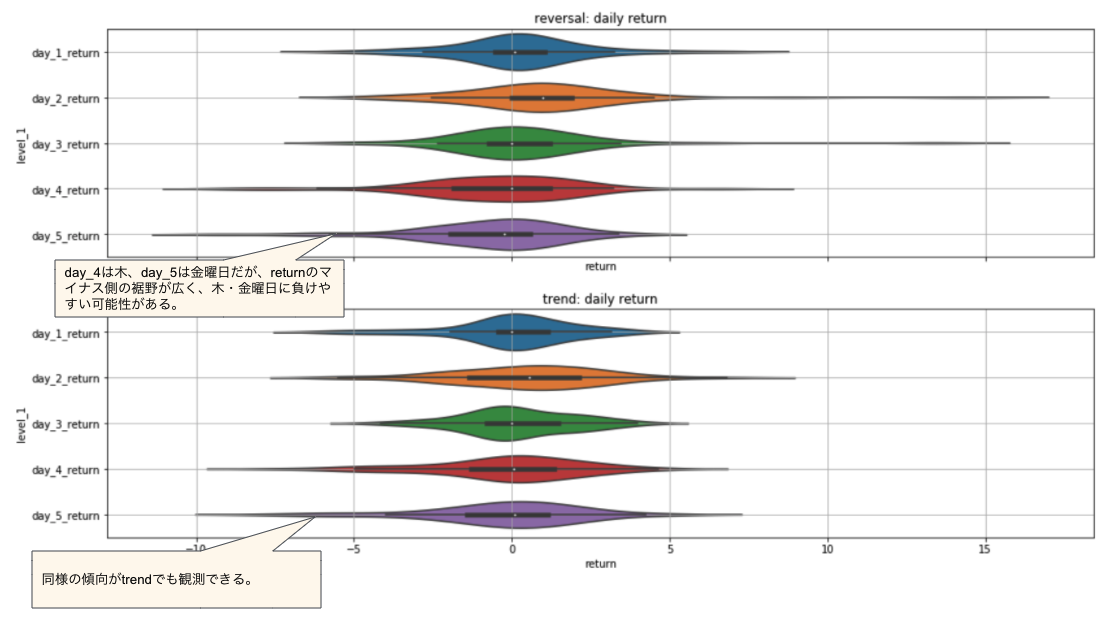
reversal/trendは木・金曜日に負ける傾向がありそうです。trendはプラス側の裾野が若干広いように思われます。これはトレンドフォローを行うと大きな勝ちが取れている可能性が示唆されます。
取引戦略によっては月曜日に大きく勝つモデルや金曜日に大きく負けるなど曜日によって強さが異なることも多く、このような曜日ごとのプロットはその銘柄の特性を知る上で、確認する価値があります。特に曜日や月などの周期でチェックする場合、負けている方(このグラフでいうととマイナス側の分布)に注目することが重要です。周期性を狙って収益を意図的に取得することは難易度の高いテクニックですが、負けの場合は理由をしっかりと分析すると防げる可能性があるためです。例えば、よくあるのが金曜日特有の週末に発生するクローズオーダーなど、機関投資家のルールにより発生する取引です。
6.収益率の時系列を累積プロット
次にいよいよ取得した収益率の時系列を累積プロットします。まず、比較対象として取引対象の全銘柄の平均週次リターンを計算します。
# 変数名を調整します。
# backtest_priceはユニバースで絞り込み済みです
df_price = backtest_price# 週毎に始値と終値を取得
df_wp = (
# start_dt以降の日付のみ計算
df_price.loc[df_price.index >= start_dt].sort_values(["Local Code", "EndOfDayQuote Date"])
# 銘柄コード毎に処理
.groupby("Local Code")
# 月曜日スタートで週にリサンプル
.resample("W-MON", label="left", closed="left")
# 始値は最初のレコード、終値は最後のレコードを取得
.agg({"EndOfDayQuote Open": "first", "EndOfDayQuote ExchangeOfficialClose": "last"})
# マルチインデックスを解除
.reset_index(level=[0])
)
# Open が 0.0 の銘柄は値段が付かなかった銘柄で、バックテストでは購入対象外であるため除外する
df_wp = df_wp.loc[df_wp.loc[:, "EndOfDayQuote Open"] != 0.0]
# 銘柄毎の週次リターンを計算
df_wp.loc[:, "universe"] = (
(
(
df_wp.loc[:, "EndOfDayQuote ExchangeOfficialClose"]
/ df_wp.loc[:, "EndOfDayQuote Open"]
)
- 1
)
* 100
)
# ユニバースの週毎のリターンを計算します。
df_universe_return = df_wp.groupby(df_wp.index)["universe"].mean().to_frame()対比軸である取引対象の全銘柄の平均週次リターンが準備できたら、今回の取引戦略の結果と一緒にプロットしてみます。
# 描画領域を定義
fig, axes = plt.subplots(1, 1, figsize=(20, 8), sharex=True, sharey=True)
# 戦略毎に処理
for k in results.keys():
# 描画位置を指定
ax = axes
# 戦略別の累積リターンを描画
results[k].set_index("date").loc[:, ["week_return"]].rename(
columns={"week_return": f"{k}: week_return"}
).cumsum().plot(ax=ax)
# ユニバースの週次リターンの累積をプロット
df_universe_return.cumsum().plot(ax=ax, color="black", label="universe")
# 表示を調整
ax.set_title("Cumulative week_return")
# グリッドを表示
ax.grid(True)
# 描画
plt.show()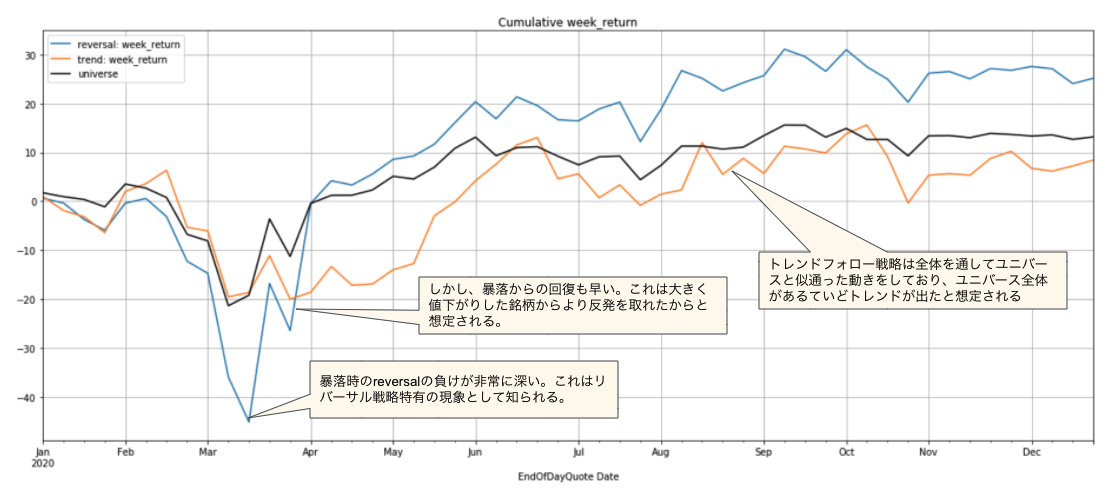
このプロットは興味深いことがわかります。
まずreversalは、3月に発生した負けが非常に大きいことがわかります。ベンチマークはおよそ-20%の負けとなっているのに対し、reversalでは-40%に到達しています。これはリターン・リバーサル戦略を採用した場合、マーケット暴落時に負けが積み重なる現象として知られています。一方、その後に0%近辺まで戻しているので3月後半から5月末にかけて、取得できたリターンは非常に大きいこともわかります。ただ、対比軸である取引対象の全銘柄の平均週次リターンには到達していません。その後、reversal戦略のユニバースに対する有意性は6月以降はあまり観測できず、12月までユニバースの平均に勝てないまま最終的に負けています。
次に、trendは3月上旬の負けがユニバースの平均と比較すると小さいことがわかります。一方、reversal戦略の場合に観測された大きな収益性は観測できず、6月にユニバースの平均と同一の水準になると、以降はreversalと同等に12月までユニバースの平均に勝てないまま最終的に負けています。
7.ユニバースとリターンの散布図をプロット
ユニバースとリターンの散布図は、マーケットの動きに対してポートフォリオの運用実績がどのように分布するかを確認するために利用します。
# 戦略毎に処理
for k in results.keys():
# 散布図をプロット
p = sns.jointplot(
x=df_universe_return.iloc[:, 0],
y=results[k].loc[:, "week_return"],
kind="reg",
height=5,
stat_func=stats.pearsonr,
)
# タイトルを設定
p.fig.suptitle(f"{k}: week_return vs universe")
# タイトル表示用に位置を調整
p.fig.subplots_adjust(top=0.95)
# 描画
plt.show()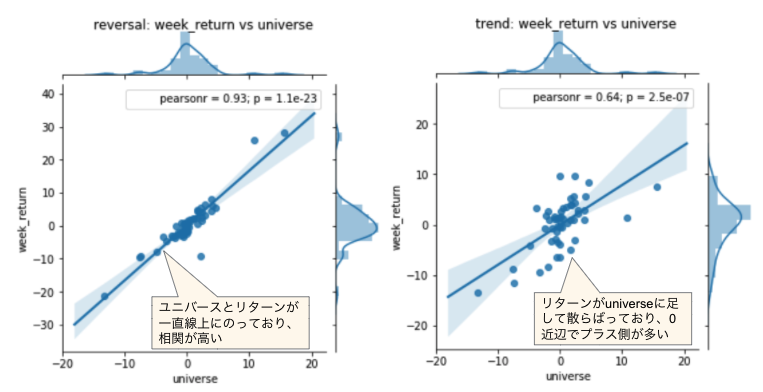
reversalはユニバースに対して、全体が下がった時に負けが大きく、ユニバースが上がった時に勝ちがわずかにユニバースを上回ることが観測できます。trendは分布が広がっており、ユニバースの影響をあまり受けていないことがわかります。また、0でリターンを稼いでいる週が多く観測出来、マーケットが動いていない時に細かく勝てている可能性が示唆されます。
8.ベータ値の算出
上記の傾向はベータを計算すると一目瞭然です。
# 結合用に保存
buff = []
# 戦略毎に処理
for k in results.keys():
# ベータを計算
res = stats.linregress(df_universe_return.iloc[:,0], results[k].loc[:, "week_return"])
# 一覧表示用にデータフレームを作成
df_beta = pd.DataFrame([res.slope], index=[k], columns=["beta"])
# インデックス名を設定
df_beta.index.name = "storategy_id"
# 保存
buff.append(df_beta)
# 結合して表示
pd.concat(buff)
reversalはベータがおよそ1.6となっており、ユニバースが10%変動すると16%程度の変動が発生する取引戦略であることがわかります。ユニバースが-20%変動したときは-32%変動しますので、暴落時の大きな負けもこのベータ値の高さで説明ができます。3月のようにドローダウンが深くなる現象は、高いベータを持つ取引戦略にはよく観測されます。trendはベータが0.8近辺となっており、reversalと比較すると低いベータとなっています。
銘柄毎に分析するための準備
最後に銘柄毎のデータを使用して分析していきます。
各銘柄毎のデータ
-
銘柄毎の運用実績の分布をプロット
-
銘柄毎のreturnの分布をプロット
-
週毎の勝ち銘柄率をプロット、統計量の算出
銘柄毎のデータを使用して分析するために必要な計算を実施します。
# 分析用データ保存用
dfs_analyze = {}
# 戦略毎に処理
for i in stocks.keys():
# 分析用にデータをコピー
df_analyze = stocks[i].copy()
# day5に必ず値が存在するように調整します
df_analyze.loc[:, ["day_1", "day_2", "day_3", "day_4", "day_5"]] = (
df_analyze.loc[:, ["day_1", "day_2", "day_3", "day_4", "day_5"]]
.replace(0.0, np.nan)
.ffill(axis=1)
)
# 終値とエントリーの差分を計算
df_analyze.loc[:, "diff"] = df_analyze.loc[:, ["entry", "day_5"]].diff(axis=1)[
"day_5"
]
# 損益を計算します
df_analyze.loc[:, "pl"] = df_analyze.loc[:, "diff"] * df_analyze.loc[:, "actual"]
# リターンを計算します
df_analyze.loc[:, "return"] = (
(df_analyze.loc[:, "day_5"] / df_analyze.loc[:, "entry"]) - 1
) * 100
# infを0.0に変換
df_analyze = df_analyze.replace(np.inf, 0.0)
# 処理結果を保存
dfs_analyze[i] = df_analyze1.銘柄毎の運用実績の分布をプロット
分析用データを表示して確認します。
dfs_analyze["reversal"].head(2)
2.銘柄毎のリターンの分布をヒストグラムでプロット
銘柄毎の各週のデータを確認します。銘柄毎のリターンの分布をヒストグラムでまずはプロットします。
# 描画領域を定義
fig, axes = plt.subplots(1, len(dfs_analyze), figsize=(8 * len(dfs_analyze), 8), sharex=True, sharey=True)
# 戦略毎に処理
for i, k in enumerate(dfs_analyze.keys()):
# 描画位置を指定
ax = axes[i]
# ヒストグラムをプロット
dfs_analyze[k].groupby(["date", "Local Code"])["return"].sum().hist(bins=50, log=True, ax=ax)
# タイトルを設定
ax.set_title(f"{k}: Weekly PL distribution")
# 描画
plt.show()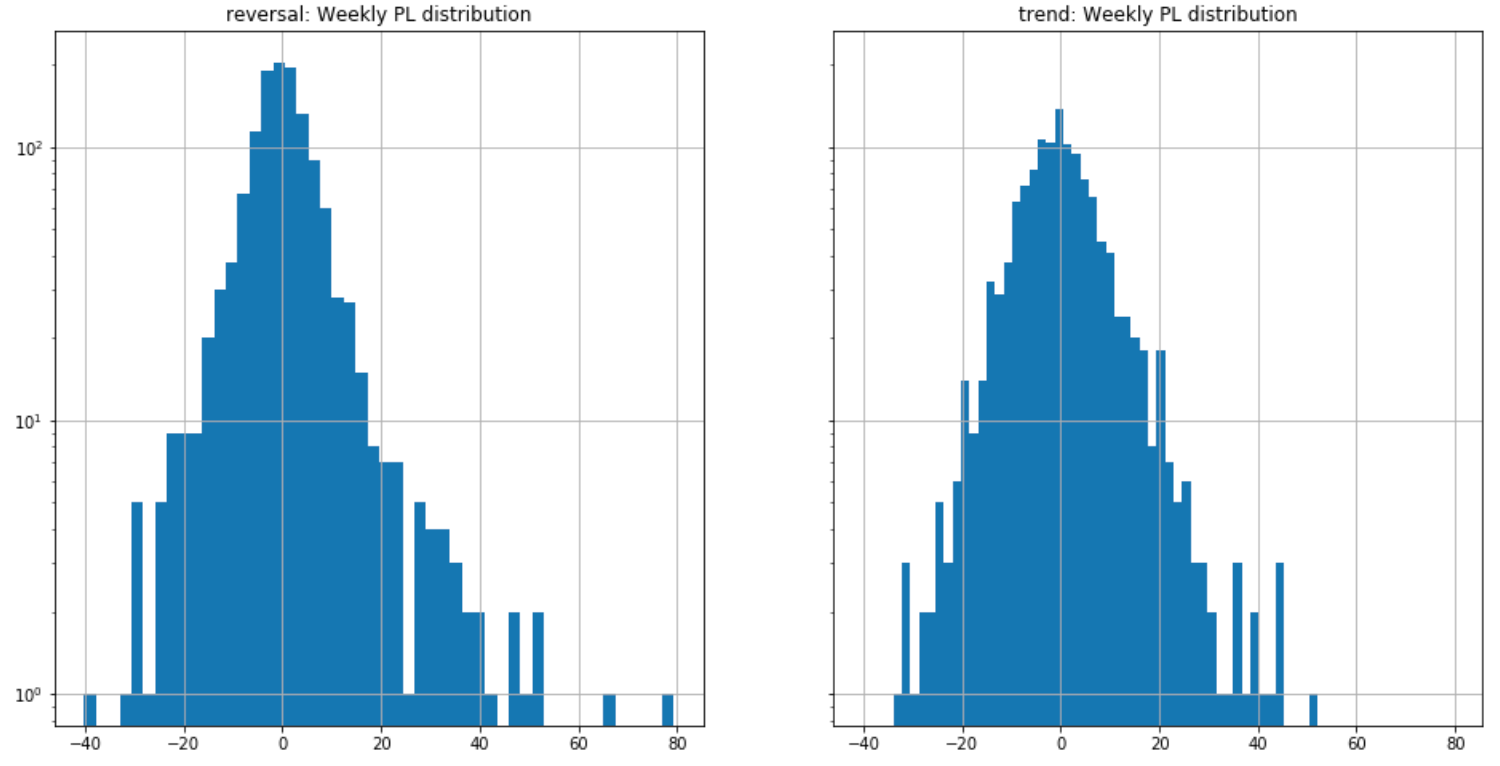
銘柄毎リターンの分布をプロットしてみましたが、ここから何か知見は得ることは難しそうです。上のプロットからもこれといった知見をえることはできません。あえて言うなら、reversalが若干trendと比較すると裾野が広い程度です。ただし、リターンを大きな勝ちに依存している戦略や、負けの裾野が非常に広い戦略などもこのプロットで観測できるため、リターンの分布は常に確認することをおすすめします。
3.週毎に勝ち銘柄率を算出、統計量の算出
最後に週毎の銘柄の勝率を確認します。
# 描画領域を定義
fig, ax = plt.subplots(1, 1, figsize=(20, 8), sharex=True, sharey=True)
# 統計量表示用
buff = []
# 戦略毎に処理
for k in dfs_analyze.keys():
# 週毎の勝ち銘柄率を計算
win_ratio = (
dfs_analyze[k]
.set_index("date")
.groupby("date")
.apply(lambda x: (x.pl > 0).sum() / x.shape[0])
.to_frame()
.rename(columns={0: f"{k}: win_ratio"})
)
# プロット
win_ratio.plot(ax=ax)
# 統計量を保存
buff.append(win_ratio.describe().T)
# ユニバースの勝ち銘柄率をプロット
df_wp.groupby(df_wp.index).apply(lambda x: (x.universe > 0).sum() / x.shape[0]).rename(
"universe"
).to_frame().plot(ax=ax, color="black")
# タイトルを設定
ax.set_title("win ratio of selected stocks")
# グリッド表示
ax.grid(True)
# 0.5に基準線を描画
ax.axhline(y=0.5, color="red")
# 描画
plt.show()
# 週毎の勝ち銘柄率の統計量
display(pd.concat(buff))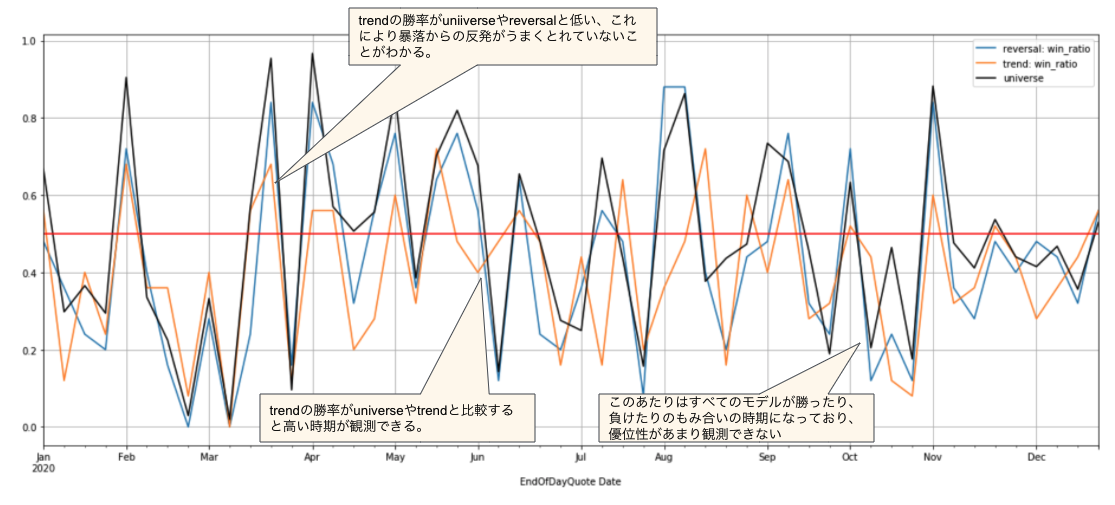
このプロットは黒線のuniverseに対してどの時期に銘柄単位で勝率が低く、どの時期に勝率が高かったを確認しています。trendは暴落後にあまり収益を得ることができませんでしたが、revesalやunivereとの差異が観測できます。
もし、銘柄単位の勝率で大きな差異が発生していないのに、収益に差異が出ている場合はその時の銘柄の勝ち幅が大きい可能性があります。また、9月以降にもみ合いになってしまった時期はこの勝率でも50%近辺で揉み合っており、取引戦略の優位性が発揮できていない時期であることがわかります。
考察
ここまででいろいろな観点からreversalとtrendの評価を実施してきました。3月末以降のリターン・リバーサル戦略が有効に働いている時期もありましたし、トレンドフォロー戦略でベータ値を低く抑える可能性があることがわかりました。
基本的にリターン・リバーサル戦略とトレンドフォロー戦略は安定して勝てる手法ではなく、リバーサル・モメンタムという代表的なファクターと密接な関係があり、マーケットの局面ごとに有効な戦略が変わっていることが知られています。ここまでの結果から、適切にリターン・リバーサル戦略とトレンドフォロー戦略をモデルで切り替えることが実現できれば、高い収益が実現できるポテンシャルがありそうです。そのような機械学習モデルの構築を検討する価値はあるでしょう。
このように様々な可視化を通して、取引戦略を評価することで、取引戦略を発展させていくことができます。
3.8. 投稿用パッケージの作成
3.8.1. 投稿用パッケージのディレクトリの作成
ここまで、モデルの作成及び評価をしてきました。ここからは、投稿用のパッケージを作成します。ランタイム環境用のモデルは以下の構成である必要がありますので、まずは必要なディレクトリを作成していきます。
.
├── model 必須 学習済モデルを置くディレクトリ
│ └── ...
├── src 必須 Python のプログラムを置くディレクトリ
│ ├── predictor.py 必須 最初にプログラムが呼び出すファイル
│ └── ... その他のファイル (ディレクトリも作成可能)
└── requirements.txt 任意# 作業用のディレクトリを設定
if 'google.colab' in sys.modules:
working_dir = "/content/drive/MyDrive/JPX_competition/Chapter03"
else:
working_dir = "."
# パッケージのrootディレクトリ
package_dir = f"{working_dir}/archive"# 必要なディレクトリを作成します
os.makedirs(f"{package_dir}/model", exist_ok=True)
os.makedirs(f"{package_dir}/src", exist_ok=True)
# 今回はmodelディレクトリに保存するファイルがないため空ファイルを作成します
open(f"{package_dir}/model/dummy.txt", mode="a").close()3.8.2. ランタイム実行用クラスの作成
notebookの各セルで実行する内容をファイルに書き出すために、jupyter notebookにマジックコマンドを追加します。
# jupyter notebookにマジックコマンドを追加します
# セル実行と同時にセル内の記載内容をファイルに書き込みます
@register_cell_magic
def writerun(line, cell):
# 書き込み先ファイルパスを取得
file_path = line.split()[-1]
# 親ディレクトリ名を取得
p_dir = os.path.dirname(file_path)
# 親ディレクトリが存在する場合は
if p_dir != "":
# ディレクトリ作成
os.makedirs(p_dir, exist_ok=True)
# cellの内容をファイルに書き込み
with open(file_path, mode="w") as f:
f.write(cell)
# cellを実行
get_ipython().run_cell(cell) 以下のコードは、ここまでに一行ずつ作成したコードを投稿用の ScoringService としてまとめて実装したものになります。また、今回は学習済モデルのパラメーターなどをファイルに書き出していないため、`get_model` メソッドでは何もせずにTrueを返しています。そして、`predict` メソッドには上記で実行したコードをコピーして貼り付けています。表示用のコードおよび作業用データのコピーについてはランタイム環境では実行する必要がないため削除しています。
jupyter notebookのセルに ScoringService クラスを作成している理由は、`ScoringService` クラスの出力するポートフォリオがこれまで検証してきたポートフォリオと同一であることの検証が容易であるためです。慣れている方は直接`predictor.py` ファイル上で作業することを好まれるかもしれません。
次のセルでは、セルの先頭で writerun マジックコマンドを指定することで、実行時にセルの内容が $package_dir/src/predictor.py ファイルに書き込まれます。すでにファイルが存在している場合は上書きされるためご注意ください。
%%writerun $package_dir/src/predictor.py
# -*- coding: utf-8 -*-
import io
import pandas as pd
class ScoringService(object):
@classmethod
def get_model(cls, model_path="../model"):
return True
@classmethod
def predict(
cls, inputs, start_dt=pd.Timestamp("2021-02-01"), strategy_id="reversal"
):
####
# データセットを読み込みます
####
# 銘柄情報読み込み
df_stock_list = pd.read_csv(inputs["stock_list"])
# 問題2のユニバース (投資対象銘柄群) 取得
codes = df_stock_list.loc[
df_stock_list.loc[:, "universe_comp2"] == True, "Local Code"
].unique()
# 価格情報読み込み、インデックス作成
df_price = pd.read_csv(inputs["stock_price"]).set_index("EndOfDayQuote Date")
# 日付型に変換
df_price.index = pd.to_datetime(df_price.index, format="%Y-%m-%d")
if "purchase_date" in inputs.keys():
# ランタイム環境では指定された投資対象日付を使用します
# purchase_dateを読み込み
df_purchase_date = pd.read_csv(inputs["purchase_date"])
# purchase_dateの最も古い日付を設定
start_dt = pd.Timestamp(
df_purchase_date.sort_values("Purchase Date").iloc[0, 0]
)
# 投資対象日の前週金曜日時点で予測を出力するため、予測出力用の日付を設定します。
pred_start_dt = pd.Timestamp(start_dt) - pd.Timedelta("3D")
# 特徴量の生成に必要な日数をバッファとして設定
n = 30
# データ絞り込み日付設定
data_start_dt = pred_start_dt - pd.offsets.BDay(n)
# 日付で絞り込み
filter_date = df_price.index >= data_start_dt
# 銘柄をユニバースで絞り込み
filter_universe = df_price.loc[:, "Local Code"].isin(codes)
# 絞り込み実施
df_price = df_price.loc[filter_date & filter_universe]
####
# シンプルな特徴量を作成します
####
# groupby を使用して処理するために並び替え
df_price.sort_values(["Local Code", "EndOfDayQuote Date"], inplace=True)
# 銘柄毎にグループにします。
grouped_price = df_price.groupby("Local Code")[
"EndOfDayQuote ExchangeOfficialClose"
]
# 銘柄毎に20営業日の変化率を作成してから、金曜日に必ずデータが存在するようにリサンプルしてフィルします
df_feature = grouped_price.apply(
lambda x: x.pct_change(20).resample("B").ffill().dropna()
).to_frame()
# 上記が比較的時間のかかる処理なので、処理済みデータを残しておきます。
df_work = df_feature # copyはランタイム実行時には不要なので削除しています
# インデックスが銘柄コードと日付になっているため、日付のみに変更します。
df_work = df_work.reset_index(level=[0])
# カラム名を変更します
df_work.rename(
columns={"EndOfDayQuote ExchangeOfficialClose": "pct_change"},
inplace=True,
)
# データをpred_start_dt以降の日付に絞り込みます
df_work = df_work.loc[df_work.index >= pred_start_dt]
####
# ポートフォリオを組成します
####
# 金曜日のデータのみに絞り込みます
df_work = df_work.loc[df_work.index.dayofweek == 4]
# 日付毎に処理するためグループ化します
grouped_work = df_work.groupby("EndOfDayQuote Date", as_index=False)
# 選択する銘柄数を指定します
number_of_portfolio_stocks = 25
# ポートフォリオの組成方法を戦略に応じて調整します
strategies = {
# リターン・リバーサル戦略
"reversal": {"asc": True},
# トレンドフォロー戦略
"trend": {"asc": False},
}
# 戦略に応じたポートフォリオを保存します
df_portfolios = {}
# strategy_id が設定されていない場合は全ての戦略のポートフォリオを作成します
if "strategy_id" not in locals():
strategy_id = None
for i in [strategy_id] if strategy_id is not None else strategies.keys():
# 日付毎に戦略に応じた上位25銘柄を選択します。
df_portfolios[i] = grouped_work.apply(
lambda x: x.sort_values(
"pct_change", ascending=strategies[i]["asc"]
).head(number_of_portfolio_stocks)
)
# 銘柄ごとの購入金額を指定
budget = 50000
# 戦略毎に処理
for i in df_portfolios.keys():
# 購入株式数を設定
df_portfolios[i].loc[:, "budget"] = budget
# インデックスを日付のみにします
df_portfolios[i].reset_index(level=[0], inplace=True)
# 金曜日から月曜日日付に変更
df_portfolios[i].index = df_portfolios[i].index + pd.Timedelta("3D")
####
# 出力を調整します
####
# 戦略毎に処理
for i in df_portfolios.keys():
# インデックス名を設定
df_portfolios[i].index.name = "date"
# 出力するカラムを絞り込みます
df_portfolios[i] = df_portfolios[i].loc[:, ["Local Code", "budget"]]
# 出力保存用
outputs = {}
# 戦略毎に処理
for i in df_portfolios.keys():
# 出力します
out = io.StringIO()
# CSV形式で出力
df_portfolios[i].to_csv(out, header=True)
# 出力を保存
outputs[i] = out.getvalue()
return outputs[strategy_id]ファイルが書き込まれていることを確認します
! ls -l $package_dir/src/出力
total 3
-rw-r--r-- 1 root root 4450 Feb 27 09:40 predictor.py作成したクラスが適切に動くかを動作確認します。 上記で1行ずつ実行した場合と同一の出力であれば良いことになります。
# 動作確認します
str_ret = ScoringService.predict(inputs, start_dt=pd.Timestamp("2020-01-01"))# 出力を確認
print("\n".join(str_ret.split("\n")[:10]))出力させます。
date,Local Code,budget
2020-01-06,4592,50000
2020-01-06,3254,50000
2020-01-06,6875,50000
2020-01-06,4571,50000
2020-01-06,7956,50000
2020-01-06,6049,50000
2020-01-06,7744,50000
2020-01-06,2395,50000
2020-01-06,3660,50000# 出力を保存
with open("chapter03-tutorial-01-class.csv", mode="w") as f:
f.write(str_ret)出力が一致していることを確認します。
assert outputs["reversal"] == str_ret3.8.3. 提出用パッケージの作成と提出
3.7.10で作成した ScoringService を predictor.py に書き込み、Zip形式で圧縮します。今回はシンプルな特徴量を使用してポートフォリオを作成しているため、学習済みのモデルファイルは存在しません。ただし、modelディレクトリは必須であるため、zipファイルには該当のディレクトリを含める必要があります。そのためには、modelファイルには何らかのダミーファイルを作成してzipファイルを作成すると良いでしょう。
以下、Zipファイル作成例になります。
$ mkdir model src
$ touch model/dummy.txt
$ ls
model src
$ zip -v submit.zip src/predictor.py model/dummy.txt# 提出用パッケージ名
package_file = "chapter03-model.zip"
# パッケージファイルパス
package_path = f"{working_dir}/{package_file}"
# zipファイルを作成
with zipfile.ZipFile(package_path, "w") as f:
# model/dummy.txtを追加
print(f"[+] add {package_dir}/model/dummy.txt to model/dummy.txt")
f.write(f"{package_dir}/model/dummy.txt", "model/dummy.txt")
# src/predictor.py を追加
print(f"[+] add {package_dir}/src/predictor.py to src/predictor.py")
f.write(f"{package_dir}/src/predictor.py", "src/predictor.py")
print(f"[+] please check {package_path}")以上で投稿用のモデルパッケージは完成です。`chapter03-model.zip` ファイルをコンペティションページから投稿してリーダーボードに掲載されることを確認しましょう。
リーダーボードに掲載されたことを確認したら、例えば、特徴量を変更してみたり、複数の特徴量それぞれから10銘柄ずつ選択するロジックを実装してみるのはどうでしょうか。いくつかの特徴量については「2.7. 特徴量の生成」で説明していますのでご参照ください。特に、「2.7.2. 定常性を意識した特徴量設計」は重要な概念ですのでご一読ください。
次章では、2章で作成した機械学習モデルを使用してポートフォリオを組成する方法について記載しています。
4. 「ファンダメンタルズ分析チャレンジ」で作成したモデルを使用してポートフォリオを構築しよう
4章では、2章の「ファンダメンタルズ分析チャレンジ」で作成したモデルを利用してポートフォリオを構築していきます。
2章で作成した最高値・最安値予測モデルが、各銘柄の株価の最高値・最安値だけではなく先行きもある程度予測できていたとしたら、ポートフォリオの組成のためのスコアとして利用しても、ある程度の効果が期待できるかもしれません。特に最安値予測はある種の最大リスクの推定であるため、リスクが最も低い銘柄に投資するという戦略は十分に収益を産み出す可能性があります。
3章ではリターン・リバーサル (逆張り) 戦略とトレンドフォロー (順張り) 戦略を採用し、その実装を行いましたが、3章は機械学習のアプローチというよりはむしろ、予測モデルを作成せずに戦略をそのまま実装しています。4章の狙いは予測モデルを利用したポートフォリオの組成方法を学ぶことです。本章は主に以下のステップで進めていきます。
1. 環境設定
2. ライブラリのロード
3. データセットの読み込み
4. 2章で作成したモデルの配置
5. 2章のpredictor.pyの変更
5.1 get_inputsの変更 (stock_fin_priceを読み込む)
5.2 get_datasetの変更 (必要なデータのみ読み込む)
5.3 get_codesの変更 (ユニバースの変更)
5.4 get_features_for_predict の変更 (stock_fin_priceを使用する)
5.5 predictの変更 (銘柄選択、出力を変更)
6. バックテストの実行
7. バックテストの評価
8. 適時開示情報を使用して特別損失銘柄を除外
9. パッケージの作成4.1. 環境設定
基本的に4章の環境設定方法は、3章に準拠しています。本章のnotebookはこちらからダウンロードしてご利用ください。なお、2章のnotebookを実行した際に最後に保存されるモデルを配置したディレクトリを ScoringService.get_model のパラメーターとして設定する必要があります。本チュートリアルの2章をそのまま実行した際の学習済みのモデルは、こちらからダウンロード可能です。
Google Colaboratoryの環境で本チュートリアルを実行する場合、最初に以下のコードを実行して Google Colaboratory 上の notebook から Google Drive にアクセスできるようにしてください。
# Google Colab環境ではGoogle Driveをマウントしてアクセスできるようにします。
import sys
if 'google.colab' in sys.modules:
# Google Drive をマウントします
from google.colab import drive
mount_dir = "/content/drive"
drive.mount(mount_dir)4.2. 必要なライブラリの読み込み
ランタイム環境とGoogle Colaboratory環境の両者で共通のライブラリを使用するためにバージョンを調整します。
!pip install --no-cache-dir joblib==1.0.1 numpy==1.19.5 pandas==1.1.5 scikit-learn==0.20.3 scipy==1.2.1 seaborn==0.9.0次に、以下のライブラリを読み込みます。
import io
import os
import pickle
import sys
import zipfile
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from scipy import stats
from sklearn.ensemble import RandomForestRegressor
from tqdm.auto import tqdm次に、本コンペティションの評価検証用のバックテストモジュールを読み込みます。バックテストモジュールの使用方法については「3.6. バックテスト環境の構築」をご参照ください。インポート時にエラーが出た場合は、sys.path に backtest.py ファイルを配置したディレクトリを追加してから再度インポートしてください。
# インポート時にエラーが出た場合は、以下のmodule_dirをbacktest.pyを配置したディレクトリに変更してください。
import sys
if 'google.colab' in sys.modules:
# Backtestを配置したディレクトリへのフルパスを指定します
module_dir = f"{mount_dir}/MyDrive/JPX_competition/Chapter03/backtest"
else:
# Backtestを配置したディレクトリへのフルパスを指定します
module_dir = "/notebook/Chapter03/backtest"
sys.path.append(module_dir)
from backtest import BacktestPandasのデータを表示する際に省略されないように設定を変更します
# 表示用の設定を変更します
%matplotlib inline
pd.options.display.max_rows = 100
pd.options.display.max_columns = 100
pd.options.display.width = 1204.3. データセット及び2章のモデル準備
4.3.1. データセットの読み込み
データセットを配置したディレクトリのパスを設定します。Google Colabをご使用の場合は Google Drive にデータセットをアップロードし、そのディレクトリを指定してください。なお、データセットの取得方法および内容については「3.4. データセットの説明」をご参照ください。
# データセットを配置したディレクトリのパスを設定
if 'google.colab' in sys.modules:
dataset_dir = f"{mount_dir}/MyDrive/JPX_competition/data_dir_comp2"
else:
dataset_dir = "/notebook/data_dir_comp2" 本コンペティションのランタイム環境におけるデータセットへのアクセスは、 ScoringService.predict() メソッドに渡されるinputsパラメーターを通して行う必要があります。そのため、以下のように本notebook環境でもランタイム環境と共通の方法でデータセットにアクセスすることで、コードが複雑になったり投稿用にコードを編集したりしなくても済むようにしています。なお、ランタイム環境では purchase_date.csv に評価対象週の初日の日付が指定されます。以下ではランタイム環境でも適切に動作するように purchase_date.csv の日付をポートフォリオの組成対象とするコードを記載します。
# 入力パラメーターを設定します。ランタイム環境での実行時と同一フォーマットにします
inputs = {
"stock_list": f"{dataset_dir}/stock_list.csv.gz",
"stock_price": f"{dataset_dir}/stock_price.csv.gz",
"stock_fin": f"{dataset_dir}/stock_fin.csv.gz",
"stock_fin_price": f"{dataset_dir}/stock_fin_price.csv.gz",
# ニュースデータ
"tdnet": f"{dataset_dir}/tdnet.csv.gz",
"disclosureItems": f"{dataset_dir}/disclosureItems.csv.gz",
"nikkei_article": f"{dataset_dir}/nikkei_article.csv.gz",
"article": f"{dataset_dir}/article.csv.gz",
"industry": f"{dataset_dir}/industry.csv.gz",
"industry2": f"{dataset_dir}/industry2.csv.gz",
"region": f"{dataset_dir}/region.csv.gz",
"theme": f"{dataset_dir}/theme.csv.gz",
# 目的変数データ
"stock_labels": f"{dataset_dir}/stock_labels.csv.gz",
}4.3.2. 2章で作成したモデルの配置
2章で作成したモデルである my_label_high_20.pkl と my_label_low_20.pkl をarchive/modelディレクトリに配置します。これらのモデルはこちらからダウンロードすることができます。
モデルを配置したディレクトリを変数に設定します。
# モデル配置ディレクトリのパスを設定
if 'google.colab' in sys.modules:
model_dir = f"{mount_dir}/MyDrive/JPX_competition/Chapter04/archive/model"
else:
model_dir = "archive/model"モデルが正しく配置されていることを以下のコードで確認します。
!ls -lh $model_dir/4.4. 2章で作成した predictor.py の変更
ここからは2章で作成した predictor.py をベースに変更していきます。なお、2章の predictor.py はこちらから取得可能です。
ここでは、predictor.pyに以下の変更を実施します。ある程度規模の大きな変更となりますが、ポートフォリオを組成するために必要な変更です。
-
get_datasetの変更 (必要なデータのみ読み込む)
-
get_codesの変更 (ユニバースの変更)
-
get_features_for_predict の変更 (stock_fin_priceを使用する)
-
get_exclude の追加 (適時開示情報を使用した銘柄選択)
-
strategy の追加 (銘柄選択)
-
predict の変更 (銘柄選択、出力を変更)
4.4.1. get_datasetの変更 (必要なデータのみ読み込む)
まずは、load_dataパラメータを追加して必要なファイルのみをロードするように変更します。
@classmethod
def get_dataset(cls, inputs, load_data):
"""
Args:
inputs (list[str]): path to dataset files
load_data (list[str]): specify loading data
Returns:
dict[pd.DataFrame]: loaded data
"""
if cls.dfs is None:
cls.dfs = {}
for k, v in inputs.items():
# 必要なデータのみ読み込みます
if k not in load_data:
continue
cls.dfs[k] = pd.read_csv(v)
# DataFrameのindexを設定します。
if k == "stock_price":
cls.dfs[k].loc[:, "datetime"] = pd.to_datetime(
cls.dfs[k].loc[:, "EndOfDayQuote Date"]
)
cls.dfs[k].set_index("datetime", inplace=True)
elif k in ["stock_fin", "stock_fin_price", "stock_labels"]:
cls.dfs[k].loc[:, "datetime"] = pd.to_datetime(
cls.dfs[k].loc[:, "base_date"]
)
cls.dfs[k].set_index("datetime", inplace=True)
return cls.dfs4.4.2. get_codesの変更 (ユニバースの変更)
次に、ユニバースを取得するためにuniverse_comp2がTrueのコードを取得するように変更 (prediction_targetから変更)します。
@classmethod
def get_codes(cls, dfs):
"""
Args:
dfs (dict[pd.DataFrame]): loaded data
Returns:
array: list of stock codes
"""
stock_list = dfs["stock_list"].copy()
# 予測対象の銘柄コードを取得
cls.codes = stock_list[stock_list["universe_comp2"] == True][
"Local Code"
].values
return cls.codes4.4.3. get_features_for_predict の変更 (stock_fin_priceを使用する)
stock_fin_priceを使用するように変更し、さらに本コンペでは週末である金曜日までのデータを利用して出力をだすため、3章でも行ったリサンプル・前方補完の処理を行った上で、金曜日のレコードのみを使用するように変更します。
@classmethod
def get_features_for_predict2(cls, dfs, code, fin_columns, start_dt=TEST_START):
"""
Args:
dfs (dict) : dict of pd.DataFrame include stock_fin, stock_price
code (int) : A local code for a listed company
fin_columns(list[str]): list of columns
start_dt (str): specify date range
Returns:
feature DataFrame (pd.DataFrame)
"""
# stock_fin_priceデータを読み込み
stock_fin_price = dfs["stock_fin_price"]
# 特定の銘柄コードのデータに絞る
feats = stock_fin_price[stock_fin_price["Local Code"] == code]
# 2章で作成したモデルの特徴量では過去60営業日のデータを使用しているため、
# 予測対象日からバッファ含めて土日を除く過去90日遡った時点から特徴量を生成します。
n = 90
# 特徴量の生成対象期間を指定
feats = feats.loc[pd.Timestamp(start_dt) - pd.offsets.BDay(n) :]
# 指定されたカラムおよびExchangeOfficialCloseに絞り込み
feats = feats.loc[
:, fin_columns + ["EndOfDayQuote ExchangeOfficialClose"]
].copy()
# 欠損値処理
feats = feats.fillna(0)
# 終値の20営業日リターン
feats["return_1month"] = feats[
"EndOfDayQuote ExchangeOfficialClose"
].pct_change(20)
# 終値の40営業日リターン
feats["return_2month"] = feats[
"EndOfDayQuote ExchangeOfficialClose"
].pct_change(40)
# 終値の60営業日リターン
feats["return_3month"] = feats[
"EndOfDayQuote ExchangeOfficialClose"
].pct_change(60)
# 終値の20営業日ボラティリティ
feats["volatility_1month"] = (
np.log(feats["EndOfDayQuote ExchangeOfficialClose"])
.diff()
.rolling(20)
.std()
)
# 終値の40営業日ボラティリティ
feats["volatility_2month"] = (
np.log(feats["EndOfDayQuote ExchangeOfficialClose"])
.diff()
.rolling(40)
.std()
)
# 終値の60営業日ボラティリティ
feats["volatility_3month"] = (
np.log(feats["EndOfDayQuote ExchangeOfficialClose"])
.diff()
.rolling(60)
.std()
)
# 終値と20営業日の単純移動平均線の乖離
feats["MA_gap_1month"] = feats["EndOfDayQuote ExchangeOfficialClose"] / (
feats["EndOfDayQuote ExchangeOfficialClose"].rolling(20).mean()
)
# 終値と40営業日の単純移動平均線の乖離
feats["MA_gap_2month"] = feats["EndOfDayQuote ExchangeOfficialClose"] / (
feats["EndOfDayQuote ExchangeOfficialClose"].rolling(40).mean()
)
# 終値と60営業日の単純移動平均線の乖離
feats["MA_gap_3month"] = feats["EndOfDayQuote ExchangeOfficialClose"] / (
feats["EndOfDayQuote ExchangeOfficialClose"].rolling(60).mean()
)
# 欠損値処理
feats = feats.fillna(0)
# 元データのカラムを削除
feats = feats.drop(["EndOfDayQuote ExchangeOfficialClose"], axis=1)
# 1B resample + ffill で金曜日に必ずレコードが存在するようにする
feats = feats.resample("B").ffill()
# 特徴量を金曜日日付のみに絞り込む
FRIDAY = 4
feats = feats.loc[feats.index.dayofweek == FRIDAY]
# 欠損値処理を行います。
feats = feats.replace([np.inf, -np.inf], 0)
# 銘柄コードを設定
feats["code"] = code
# 生成対象日以降の特徴量に絞る
feats = feats.loc[pd.Timestamp(start_dt) :]
return feats4.4.4. get_exclude の追加 (適時開示情報を使用した銘柄選択)
本コンペティションでは適時開示情報がデータとして提供されています。適時開示情報には様々な種類があり disclosureItems.csv.gz の中には適時開示資料の公開項目コードが記載されています。公開項目のなかには株価に大きな影響を与えるものもあります。
ここでは例として特別損失を開示した銘柄をその週およびその翌週にはポートフォリオに組み入れないことを試してみます。特別損失とは災害など企業の通常の業務外で発生した一過性の損失のことをいいます。市場が想定していなかった一過性の損失が発表された場合、その銘柄の株価は下がるため除外することで損失を回避できるとの仮説を設定しています。
@classmethod
def get_exclude(
cls,
df_tdnet, # tdnetのデータ
start_dt=None, # データ取得対象の開始日、Noneの場合は制限なし
end_dt=None, # データ取得対象の終了日、Noneの場合は制限なし
lookback=7, # 除外考慮期間 (days)
target_day_of_week=4, # 起点となる曜日
):
# 特別損失のレコードを取得
special_loss = df_tdnet[df_tdnet["disclosureItems"].str.contains('201"')].copy()
# 日付型を調整
special_loss["date"] = pd.to_datetime(special_loss["disclosedDate"])
# 処理対象開始日が設定されていない場合はデータの最初の日付を取得
if start_dt is None:
start_dt = special_loss["date"].iloc[0]
# 処理対象終了日が設定されていない場合はデータの最後の日付を取得
if end_dt is None:
end_dt = special_loss["date"].iloc[-1]
# 処理対象日で絞り込み
special_loss = special_loss[
(start_dt <= special_loss["date"]) & (special_loss["date"] <= end_dt)
]
# 出力用にカラムを調整
res = special_loss[["code", "disclosedDate", "date"]].copy()
# 銘柄コードを4桁にする
res["code"] = res["code"].astype(str).str[:-1]
# 予測の基準となる金曜日の日付にするために調整
res["remain"] = (target_day_of_week - res["date"].dt.dayofweek) % 7
res["start_dt"] = res["date"] + pd.to_timedelta(res["remain"], unit="d")
res["end_dt"] = res["start_dt"] + pd.Timedelta(days=lookback)
columns = ["code", "date", "start_dt", "end_dt"]
return res[columns].reset_index(drop=True)4.4.5. strategy の追加 (銘柄選択)
銘柄の選択には2章で作成した最高値・最安値モデルで予測したpred列(最高値・最安値への変化率)の値が大きい(最安値モデルの場合は小さい)上位25銘柄を採用しています。そのため、以下のようにstrategyメソッドでpred列を作成する方法により選択される銘柄を調整しています。
ここでは、以下の6種類の銘柄選択方法を実装します。
-
最高値モデル出力に最安値モデル出力を足して使用
-
最高値モデルの出力を使用
-
最安値モデルの出力を使用
-
最高値モデル出力に最安値モデル出力を足して使用し、特別損失について開示された銘柄を除外
-
最高値モデルの出力を使用し、特別損失について開示された銘柄銘柄を除外
-
最安値モデルの出力を使用し、特別損失について開示された銘柄を除外
最高値モデルは潜在的な収益性を、最安値モデルは潜在的なリスクを推定していると想定した場合、1はシンプルにそれを足し合わせることで潜在的なリスクを抑えつつ、高い収益性を持つ銘柄を探しています。もし最高値・最安値の予測が上手く働いていたら、この方法が大きな収益を達成できるはずです。2は最大の収益性を持つ銘柄、3は最もリスクが低い銘柄が採用されると想定され、それぞれのモデルの収益性を確認することができます。
4,5,6は1,2,3のそれぞれの戦略から特別損失を開示した銘柄をポートフォリオの組成対象から除外することで、特別損失開示による株価の下落を回避しポートフォリオの利益を向上できるとの仮説を検証しています。後ほど、これらの仮説の検証を簡単なバックテストを通して実施します。
@classmethod
def strategy(cls, strategy_id, df, df_tdnet):
df = df.copy()
# 銘柄選択方法選択
if strategy_id in [1, 4]:
# 最高値モデル + 最安値モデル
df.loc[:, "pred"] = df.loc[:, "label_high_20"] + df.loc[:, "label_low_20"]
elif strategy_id in [2, 5]:
# 最高値モデル
df.loc[:, "pred"] = df.loc[:, "label_high_20"]
elif strategy_id in [3, 6]:
# 最高値モデル
df.loc[:, "pred"] = df.loc[:, "label_low_20"]
else:
raise ValueError("no strategy_id selected")
# 特別損失を除外する場合
if strategy_id in [4, 5, 6]:
# 特別損失が発生した銘柄一覧を取得
df_exclude = cls.get_exclude(df_tdnet)
# 除外用にユニークな列を作成します。
df_exclude.loc[:, "date-code_lastweek"] = df_exclude.loc[:, "start_dt"].dt.strftime("%Y-%m-%d-") + df_exclude.loc[:, "code"]
df_exclude.loc[:, "date-code_thisweek"] = df_exclude.loc[:, "end_dt"].dt.strftime("%Y-%m-%d-") + df_exclude.loc[:, "code"]
df.loc[:, "date-code_lastweek"] = (df.index - pd.Timedelta("7D")).strftime("%Y-%m-%d-") + df.loc[:, "code"].astype(str)
df.loc[:, "date-code_thisweek"] = df.index.strftime("%Y-%m-%d-") + df.loc[:, "code"].astype(str)
# 特別損失銘柄を除外
df = df.loc[~df.loc[:, "date-code_lastweek"].isin(df_exclude.loc[:, "date-code_lastweek"])]
df = df.loc[~df.loc[:, "date-code_thisweek"].isin(df_exclude.loc[:, "date-code_thisweek"])]
# 予測出力を降順に並び替え
df = df.sort_values("pred", ascending=False)
# 予測出力の大きいものを取得
df = df.groupby("datetime").head(30)
return df4.4.6. predictの変更 (銘柄選択、出力を変更)
以下では、 predictor.py の predict メソッド出力についてポートフォリオを出力するように変更し、予測出力から銘柄を選択するロジックを追加しています。ランタイム環境では purchase_date で指定された日付のポートフォリオを作成するように変更しています。
@classmethod
def predict(
cls,
inputs,
labels=None,
codes=None,
start_dt=TEST_START,
load_data=["stock_list", "stock_fin", "stock_fin_price", "stock_price", "tdnet"],
fin_columns=None,
strategy_id=1,
):
"""Predict method
Args:
inputs (dict[str]): paths to the dataset files
labels (list[str]): target label names
codes (list[int]): traget codes
start_dt (str): specify date range
load_data (list[str]): specify loading data
fin_columns (list[str]): specify feature columns
strategy_id (int): specify strategy
Returns:
str: Inference for the given input.
"""
if fin_columns is None:
fin_columns = [
"Result_FinancialStatement FiscalYear",
"Result_FinancialStatement NetSales",
"Result_FinancialStatement OperatingIncome",
"Result_FinancialStatement OrdinaryIncome",
"Result_FinancialStatement NetIncome",
"Result_FinancialStatement TotalAssets",
"Result_FinancialStatement NetAssets",
"Result_FinancialStatement CashFlowsFromOperatingActivities",
"Result_FinancialStatement CashFlowsFromFinancingActivities",
"Result_FinancialStatement CashFlowsFromInvestingActivities",
"Forecast_FinancialStatement FiscalYear",
"Forecast_FinancialStatement NetSales",
"Forecast_FinancialStatement OperatingIncome",
"Forecast_FinancialStatement OrdinaryIncome",
"Forecast_FinancialStatement NetIncome",
"Result_Dividend FiscalYear",
"Result_Dividend QuarterlyDividendPerShare",
"Result_Dividend AnnualDividendPerShare",
"Forecast_Dividend FiscalYear",
"Forecast_Dividend QuarterlyDividendPerShare",
"Forecast_Dividend AnnualDividendPerShare",
]
# データ読み込み
if cls.dfs is None:
print("[+] load data")
cls.get_dataset(inputs, load_data)
cls.get_codes(cls.dfs)
# 予測対象の銘柄コードと目的変数を設定
if codes is None:
codes = cls.codes
if labels is None:
labels = cls.TARGET_LABELS
if "purchase_date" in inputs.keys():
# ランタイム環境では指定された投資対象日付を使用します
# purchase_dateを読み込み
df_purchase_date = pd.read_csv(inputs["purchase_date"])
# purchase_dateの最も古い日付を設定
start_dt = pd.Timestamp(
df_purchase_date.sort_values("Purchase Date").iloc[0, 0]
)
# 予測対象日を調整
# start_dtにはポートフォリオの購入日を指定しているため、
# 予測に使用する前週の金曜日を指定します。
start_dt = pd.Timestamp(start_dt) - pd.Timedelta("3D")
# 特徴量を作成
print("[+] generate feature")
buff = []
for code in tqdm(codes):
buff.append(
cls.get_features_for_predict2(cls.dfs, code, fin_columns, start_dt)
)
feats = pd.concat(buff)
# 結果を以下のcsv形式で出力する
# 1列目:date
# 2列目:Local Code
# 3列目:budget
# headerあり、2列目3列目はint64
# 日付と銘柄コードに絞り込み
df = feats.loc[:, ["code"]].copy()
# 購入金額を設定 (ここでは一律50000とする)
df.loc[:, "budget"] = 50000
# 特徴量カラムを指定
feature_columns = ScoringService.get_feature_columns(cls.dfs, feats)
# 目的変数毎に予測
print("[+] predict")
for label in tqdm(labels):
# 予測実施
df[label] = ScoringService.models[label].predict(feats[feature_columns])
# 出力対象列に追加
# 銘柄選択方法選択
df = cls.strategy(strategy_id, df, cls.dfs["tdnet"])
# 日付順に並び替え
df.sort_index(kind="mergesort", inplace=True)
# 月曜日日付に変更
df.index = df.index + pd.Timedelta("3D")
# 出力用に調整
df.index.name = "date"
df.rename(columns={"code": "Local Code"}, inplace=True)
df.reset_index(inplace=True)
# 出力対象列を定義
output_columns = ["date", "Local Code", "budget"]
out = io.StringIO()
df.to_csv(out, header=True, index=False, columns=output_columns)
return out.getvalue()4.4.7. 予測の実行
ここまででソースコードの変更が完了したら、いよいよモデルを実行します。まず、対象期間を設定します。2020-01-01を指定していますが、予測の出力される日はここまでの実装により月曜日の日付のみになるはずです。
# 対象期間を設定
start_dt = pd.Timestamp("2020-01-01")
# 学習済みモデルを読み込みます
ScoringService.get_model("archive/model")
# 予測を実行します
str_ret = ScoringService.predict(inputs, start_dt=start_dt, strategy_id=1)
# 出力を確認
print("\n".join(str_ret.split("\n")[:10]))出力を確認すると、月曜日の日付である2020-01-06で出力されていることがわかります。またbudgetが一律50000円となっていることも確認できまます。想定通りの結果です。
date,Local Code,budget
2020-01-06,4482,50000
2020-01-06,7679,50000
2020-01-06,2980,50000
2020-01-06,3966,50000
2020-01-06,4479,50000
2020-01-06,6049,50000
2020-01-06,4369,50000
2020-01-06,4488,50000
2020-01-06,3793,50000次で実施するバックテストのために結果をCSVファイルに保存しておきます。
# 出力を保存
with open("chapter03-tutorial-02-backtest-1.csv", mode="w") as f:
f.write(str_ret)4.5. バックテスト
4.5.1. バックテストの実行
本コンペティションの Public LB および Private LB と同等の評価ロジックを実装したバックテスト用の backtest.py ファイルを使用して、作成したポートフォリオを評価します。バックテストの使用法などの詳細は「3.6. バックテスト」をご参照ください。
初めにバックテストを使用する際に必要なデータを準備します。バックテストの実行には以下の3つのデータが必要になります。
-
ユニバース (stock_list.csv.gz)
-
株価 (stock_price.csv.gz)
-
テスト対象のポートフォリオ
Backtest.prepare_data に1および2のデータを保存しているディレクトリへのパスを指定して、必要なデータをロードします。
# データを保存しているディレクトリを指定します。
backtest_dataset_dir = dataset_dir
# バックテストに必要なデータを読み込みます。
backtest_codes, backtest_price = Backtest.prepare_data(backtest_dataset_dir)Backtest.load_submit にバックテスト対象のポートフォリオを保存したファイルへのパスを指定して読み込みます。`load_submit` ではデータを読み込み時にフォーマットのチェックをしたり、レコード順を付与する等、バックテスト実行のための前処理を実施しています。
# 先ほど出力したポートフィリオデータを読み込みます
df_submit = Backtest.load_submit("chapter03-tutorial-02-backtest-1.csv")3つのデータを指定してバックテストを実行します。
# バックテスト結果保存用
results = {}
stocks = {}results[1], stocks[1] = Backtest.run(df_submit.loc[start_dt:], backtest_codes, backtest_price)結果を確認します。うまく結果が取得できていることが確認できます。
# バックテスト結果のサマリー
results[1].head(3)
# 銘柄毎の情報
stocks[1].head(3)
次に、銘柄選択の方法を変えてポートフォリオを組成します。1はすでに取得できていますので2、3も取得します。
-
最高値モデル出力に最安値モデル出力を足して使用
-
最高値モデルの出力を使用
-
最安値モデルの出力を使用
# 戦略毎に処理
for strategy_id in tqdm([2, 3]):
# ポートフォリオ組成
str_ret = ScoringService.predict(inputs, start_dt=start_dt, strategy_id=strategy_id)
# ポートフォリオを保存
with open(f"chapter03-tutorial-02-backtest-{strategy_id}.csv", mode="w") as f:
f.write(str_ret)
# 戦略毎に処理
for strategy_id in tqdm([2, 3]):
# ポートフォリオを読み込み
df_submit = Backtest.load_submit(f"chapter03-tutorial-02-backtest-{strategy_id}.csv")
# バックテスト実行
results[strategy_id], stocks[strategy_id] = Backtest.run(df_submit.loc[start_dt:], backtest_codes, backtest_price)4.5.2. バックテストの評価
上記のバックテストを実行して取得した、週毎のリターン情報と各銘柄毎の購入結果数の情報を評価します。各項目の定義については「3.6.4. バックテストの評価軸と取引戦略」をご参照ください。
以下では、結果の評価として以下を実施します。
週毎のリターンデータ
-
週毎の運用実績の分布をプロット (本コンペティションの評価項目)
-
週毎の運用実績の統計量
-
週毎の勝率・ペイオフレシオ・シャープレシオ
-
週毎に曜日別のリターンをプロット
-
週毎のリターンの累積プロット
-
ユニバースとの散布図
-
ユニバースに対するベータを計算
各銘柄毎のデータ
-
銘柄毎の運用実績の分布をプロット
-
銘柄毎のreturnの分布をプロット
-
週毎の勝ち銘柄率をプロット
-
週毎の勝ち銘柄率の統計量
週毎の運用実績の分布をプロット
まず、週毎の運用実績の分布をヒストグラムで確認します。ここから先の解析は、「1.最高値モデル出力に最安値モデル出力を足して使用」、「2.最高値モデルの出力を使用」、「3.最安値モデルの出力を使用」の3種類を解析しており、特別損失銘柄を除外したポートフォリオ(4〜6)の解析は最後に実施します。
# 描画領域を定義
fig, axes = plt.subplots(1, len(results), figsize=(8 * len(results), 8), sharex=True, sharey=True)
# 戦略毎に処理
for i, k in enumerate(results.keys()):
# 描画位置を指定
ax = axes[i]
# 分布をプロット
results[k].week_pl.hist(bins=25, ax=ax)
# タイトルを設定
ax.set_title(f"{k}: week pl distribution")
# 描画
plt.show()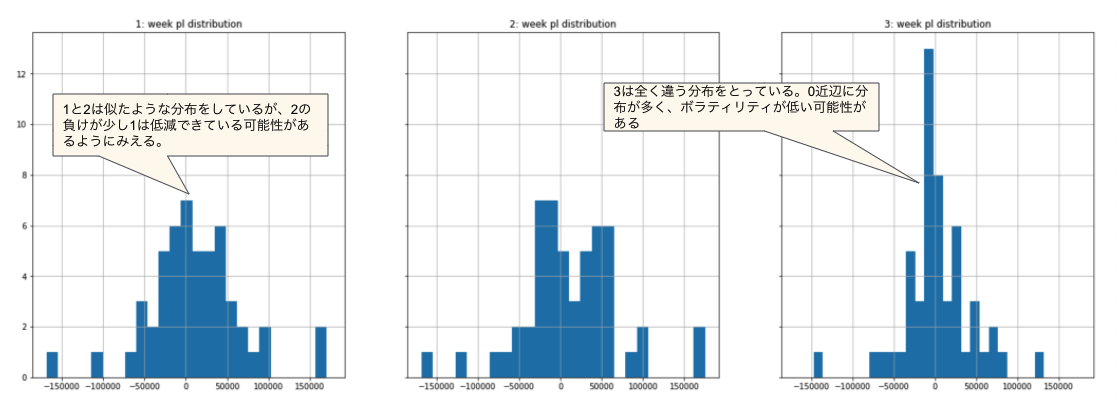
1及び2の戦略は似たような分布をしていることが確認できます。最安値モデルを利用している3は、1や2とは大きく分布が異なっており、分布が狭く運用実績が0近辺に集中していることがわかります。すなわち、3の戦略では、ボラティリティが低い銘柄を中心に採用している可能性があります。
週毎の運用実績の統計量を算出
次に、週毎の運用実績の統計量を算出します。
# week_plの分布の統計量
# 結合用データ保存
buff = []
# ストラテジー毎に処理
for k in results.keys():
# week_plの統計量を取得します。
df = results[k].loc[:, ["week_pl"]].describe().T
# インデックスを編集してストラテジーのIDにする
df.index = [k]
# インデックス名変更
df.index.name = "strategy_id"
# 結合用に保存
buff.append(df)
# 結合して表示
pd.concat(buff)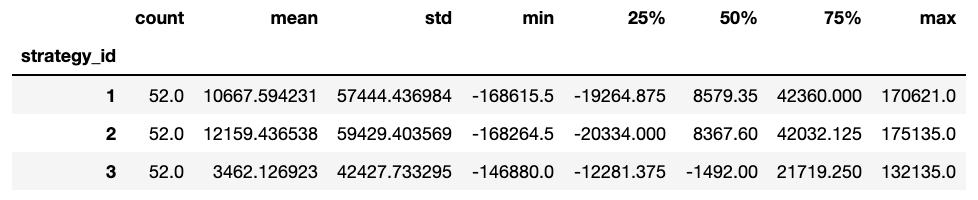
分布情報を数値で確認すると、先程と同様に1及び2の分布情報が似ていることが確認できます。異なる点として25%分位点を比較すると、1の戦略は2の戦略よりも負けを若干抑えることができている可能性が示唆されます。2の戦略では、1の戦略よりも平均が大きくなっています。結果として、1の戦略は2の戦略よりも収益性は劣るものの、リスクコントロールができている可能性が示唆されています。また、3の戦略の結果は平均が1及び2の戦略より低く、25%及び75%分位点も1及び2の戦略よりも狭い分布となっていることがわかります。
週毎の勝率、ペイオフレシオ、シャープレシオを算出
他のメトリクスも確認していきましょう。週毎の勝率、ペイオフレシオ、シャープレシオを算出します。
# 結合用データ保存
buff = []
# 戦略毎に処理
for k in results.keys():
df_return = results[k]
# 計算結果保存用
d = {}
# 件数
d["count"] = df_return.shape[0]
# 勝率
d["win_ratio"] = (
df_return.loc[df_return.loc[:, "week_return"] > 0].shape[0] / d["count"]
)
# ペイオフレシオ
d["payoff_ratio"] = df_return.loc[
df_return.loc[:, "week_return"] > 0, "week_return"
].mean() / (
-1 * df_return.loc[df_return.loc[:, "week_return"] <= 0, "week_return"].mean()
)
# シャープレシオ
d["sharp"] = (
df_return.loc[:, "week_return"].mean() / df_return.loc[:, "week_return"].std()
)
# 平均PL
d["avgPL"] = df_return.loc[:, "week_pl"].mean()
# week_plの合計
d["PL"] = df_return.loc[:, "week_pl"].sum()
# strategy_idを設定
df = pd.DataFrame([d], index=[k])
# インデックス名を指定
df.index.name = "strategy_id"
# 結合用に保存
buff.append(df)
# 結合して表示
pd.concat(buff)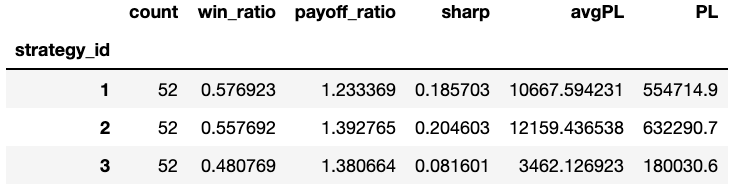
1及び2の戦略の結果はこちらでも似通っています。3の戦略は勝率も低く、運用実績も低いため、今のところ最安値を単体で利用する手法が機能しているようには見えません。
週毎に曜日別のリターンをプロット
週毎の1日目から5日目までのリターンの推移をプロットし、曜日毎に勝ち負けの分布に差異が無いかを確認しています。3章と同じようにseabornのバイオリンプロット(リンク)を利用します。
# 描画領域を定義
fig, axes = plt.subplots(len(results), 1, figsize=(15, 4 * len(results)), sharex=True, sharey=True)
# 戦略毎に処理
for i, k in enumerate(results.keys()):
# 描画位置を指定
ax = axes[i]
# 箱が見やすいように横方向を指定してプロット
sns.violinplot(x="return", y="level_1", data=dfs_plot[k], ax=ax, orient="h")
# タイトルを設定
ax.set_title(f"{k}: daily return")
# グリッドを表示
ax.grid(True)
# 文字が重なって読みにくいので間隔調整
fig.tight_layout(pad=2.0)
# 描画
plt.show()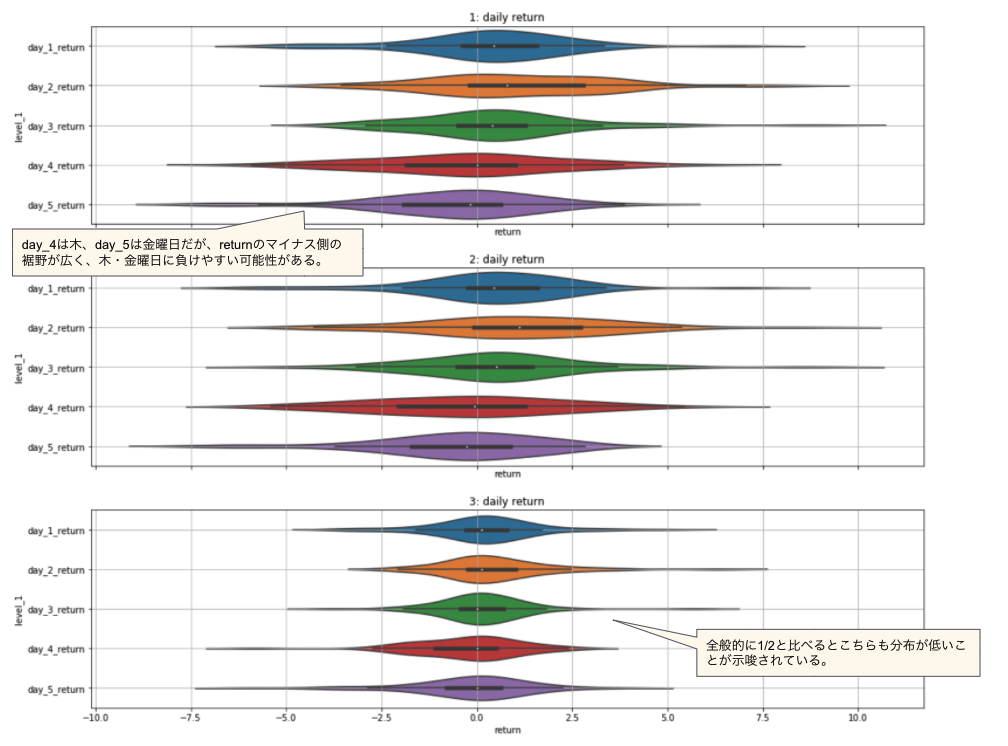
この結果から1及び2の戦略は、木曜日・金曜日の負けが大きそうなことがわかります。予測モデルを利用する場合、週の後半に負けているのはその予測モデルの効果が後半で薄れている可能性を示唆していることもあるので注意が必要です。このグラフにも若干その傾向が観測されるため、何らかの改善を実施した場合に、この結果がどうなっているかを確認する価値があります。3の戦略は1及び2の戦略と比較すると分布が狭いことが確認できます。
収益率の時系列を累積プロット
次に、取得した収益率の時系列を累積プロットします。まず、比較対象であるベンチマークとして取引対象の全銘柄の平均週次リターンを計算します。
# 変数名を調整します。
# backtest_priceはユニバースで絞り込み済みです
df_price = backtest_price# 週毎に始値と終値を取得
df_wp = (
# start_dt以降の日付のみ計算
df_price.loc[df_price.index >= start_dt].sort_values(["Local Code", "EndOfDayQuote Date"])
# 銘柄コード毎に処理
.groupby("Local Code")
# 月曜日スタートで週にリサンプル
.resample("W-MON", label="left", closed="left")
# 始値は最初のレコード、終値は最後のレコードを取得
.agg({"EndOfDayQuote Open": "first", "EndOfDayQuote ExchangeOfficialClose": "last"})
# マルチインデックスを解除
.reset_index(level=[0])
)
# Open が 0.0 の銘柄は値段が付かなかった銘柄で、バックテストでは購入対象外であるため除外する
df_wp = df_wp.loc[df_wp.loc[:, "EndOfDayQuote Open"] != 0.0]
# 銘柄毎の週次リターンを計算
df_wp.loc[:, "universe"] = (
(
(
df_wp.loc[:, "EndOfDayQuote ExchangeOfficialClose"]
/ df_wp.loc[:, "EndOfDayQuote Open"]
)
- 1
)
* 100
)
# ユニバースの週毎のリターンを計算します。
df_universe_return = df_wp.groupby(df_wp.index)["universe"].mean().to_frame()ベンチマークとして取引対象の全銘柄の平均週次リターンが準備できたら、今回の取引戦略の結果と一緒にプロットしてみます。
# 描画領域を定義
fig, axes = plt.subplots(1, 1, figsize=(20, 8), sharex=True, sharey=True)
# 戦略毎に処理
for k in results.keys():
# 描画位置を指定
ax = axes
# 戦略別の累積リターンを描画
results[k].set_index("date").loc[:, ["week_return"]].rename(
columns={"week_return": f"{k}: week_return"}
).cumsum().plot(ax=ax)
# ユニバースの週次リターンの累積をプロット
df_universe_return.cumsum().plot(ax=ax, color="black", label="universe")
# 表示を調整
ax.set_title("Cumulative week_return")
# グリッドを表示
ax.grid(True)
# 描画
plt.show()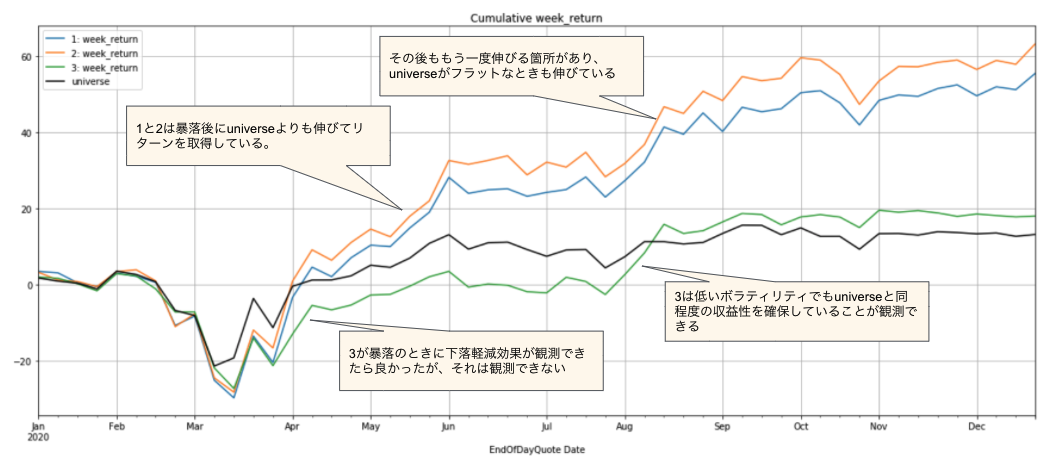
このプロットからは複数の事がわかります。まず1及び2の戦略は想定通り、極めて似通った結果となっています。1の戦略は最安値モデルの結果も足しているため、2の最高値モデルのみを用いたポートフォリオよりもドローダウンが小さいことを期待していましたが、3月の暴落時の結果を見る限り、その効果は観測されていません。これは、3の最安値モデルでも暴落時に下落低減効果が観測できないため、3の戦略では残念ながら3月の暴落の対処にはならなかったようです。
1及び2の戦略は3月以降の反発で大きく収益を上げています。特にユニバースがほぼフラットになった6月以降も1及び2の戦略は高い収益をあげており、マーケットがフラットな状況でも銘柄選択により収益を上げる力がある可能性が示唆されます。
また、3の戦略は一見するとユニバースとほぼ同じ収益に見えますが、3月以降ほぼドローダウンが発生しないことは注目に値します。これは低いボラティリティの銘柄を優先的に採用したときなどに見られる現象で、実際に収益曲線が安定していることからも、3の戦略自体もアンサンブルなどのデータとしては有望な可能性があります。
ユニバースとリターンの散布図をプロット
ユニバースとリターンの散布図をチェックします。ユニバースとリターンの散布図は、マーケットの動きに対してポートフォリオの運用実績がどのように分布するかを確認するために利用します。
# 戦略毎に処理
for k in results.keys():
# 散布図をプロット
p = sns.jointplot(
x=df_universe_return.iloc[:, 0],
y=results[k].loc[:, "week_return"],
kind="reg",
height=5,
stat_func=stats.pearsonr,
)
# タイトルを設定
p.fig.suptitle(f"{k}: week_return vs universe")
# タイトル表示用に位置を調整
p.fig.subplots_adjust(top=0.95)
# 描画
plt.show()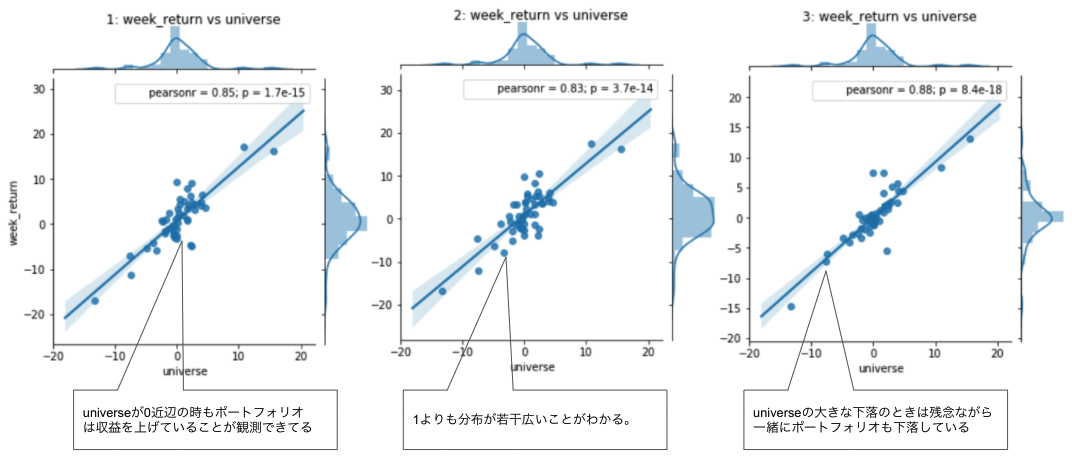
1の戦略からはユニバースが0のときも収益を上げる力がある傾向が観測できます。2の戦略の分布は1よりも広く、これは高いボラティリティの銘柄を利用している可能性が示唆されます。3の戦略はユニバースの下落のときは一緒に負けていることが観測できます。もしユニバースが下落しても、下落を抑えることができていれば、3の戦略はリスク回避用のモデルとして理想的な結果でしたが、そのような効果までは観測できませんでした。
ベータ値の算出
最後にベータを計算しましょう。
# 結合用に保存
buff = []
# 戦略毎に処理
for k in results.keys():
# ベータを計算
res = stats.linregress(df_universe_return.iloc[:,0], results[k].loc[:, "week_return"])
# 一覧表示用にデータフレームを作成
df_beta = pd.DataFrame([res.slope], index=[k], columns=["beta"])
# インデックス名を設定
df_beta.index.name = "storategy_id"
# 保存
buff.append(df_beta)
# 結合して表示
pd.concat(buff)
1及び2の戦略は、1.2近辺の高ベータなストラテジーであることがわかります。3の戦略は低いボラティリティの銘柄をポートフォリオに採用するストラテジー特有の傾向である低いベータ値が観測できています。
銘柄毎に分析するための準備
次に、銘柄毎のデータを使用して分析します。ここでは、銘柄毎のデータを使用して分析するために必要な計算を実施しています。
# 分析用データ保存用
dfs_analyze = {}
# 戦略毎に処理
for i in stocks.keys():
# 分析用にデータをコピー
df_analyze = stocks[i].copy()
# day5に必ず値が存在するように調整します
df_analyze.loc[:, ["day_1", "day_2", "day_3", "day_4", "day_5"]] = (
df_analyze.loc[:, ["day_1", "day_2", "day_3", "day_4", "day_5"]]
.replace(0.0, np.nan)
.ffill(axis=1)
)
# 終値とエントリーの差分を計算
df_analyze.loc[:, "diff"] = df_analyze.loc[:, ["entry", "day_5"]].diff(axis=1)[
"day_5"
]
# 損益を計算します
df_analyze.loc[:, "pl"] = df_analyze.loc[:, "diff"] * df_analyze.loc[:, "actual"]
# リターンを計算します
df_analyze.loc[:, "return"] = (
(df_analyze.loc[:, "day_5"] / df_analyze.loc[:, "entry"]) - 1
) * 100
# infを0.0に変換
df_analyze = df_analyze.replace(np.inf, 0.0)
# 処理結果を保存
dfs_analyze[i] = df_analyze分析用データを表示して、うまく計算ができているかを確認します。
dfs_analyze[1].head(2)
問題なく計算ができているようです。
銘柄毎のリターンの分布をヒストグラムでプロット
銘柄ごとのリターンの分布をヒストグラムでプロットします。
# 描画領域を定義
fig, axes = plt.subplots(1, len(dfs_analyze), figsize=(8 * len(dfs_analyze), 8), sharex=True, sharey=True)
# 戦略毎に処理
for i, k in enumerate(dfs_analyze.keys()):
# 描画位置を指定
ax = axes[i]
# ヒストグラムをプロット
dfs_analyze[k].groupby(["date", "Local Code"])["return"].sum().hist(bins=50, log=True, ax=ax)
# タイトルを設定
ax.set_title(f"{k}: Weekly PL distribution")
# 描画
plt.show()
ここからはあまりはっきりとした傾向はわかりませんが、1の戦略の分布が若干右側に広く大勝ちした銘柄を選択できている可能性が示唆されます。3の戦略はやはり銘柄個別で見ても分布が狭く、ボラティリティが低い銘柄を採用しているようです。
週毎に勝ち銘柄率を算出
最後に週毎の銘柄の勝率を確認します。
# 描画領域を定義
fig, ax = plt.subplots(1, 1, figsize=(20, 8), sharex=True, sharey=True)
# 統計量表示用
buff = []
# 戦略毎に処理
for k in dfs_analyze.keys():
# 週毎の勝ち銘柄率を計算
win_ratio = (
dfs_analyze[k]
.set_index("date")
.groupby("date")
.apply(lambda x: (x.pl > 0).sum() / x.shape[0])
.to_frame()
.rename(columns={0: f"{k}: win_ratio"})
)
# プロット
win_ratio.plot(ax=ax)
# 統計量を保存
buff.append(win_ratio.describe().T)
# ユニバースの勝ち銘柄率をプロット
df_wp.groupby(df_wp.index).apply(lambda x: (x.universe > 0).sum() / x.shape[0]).rename(
"universe"
).to_frame().plot(ax=ax, color="black")
# タイトルを設定
ax.set_title("win ratio of selected stocks")
# グリッド表示
ax.grid(True)
# 0.5に基準線を描画
ax.axhline(y=0.5, color="red")
# 描画
plt.show()
# 週毎の勝ち銘柄率の統計量
display(pd.concat(buff))
このプロットからいくつかおもしろいことがわかります。まず、1/2のストラテジーは6月から10月にかけて収益を上げていましたが、この時期に勝率がユニバースよりも高かったわけではないことがわかります。むしろ銘柄単位で見ると勝率はユニバースの平均よりも若干低い事がわかります。つまり、この期間に1/2のストラテジーは勝率で稼いだわけではなく、銘柄ごとのリターンが大きかったことが推測されます。
これはどのような銘柄を選択していたかを調査することによって、どのあたりに収益性の厳選があるかを考えるヒントになります。このような傾向が観測されたらファクター分析などを利用して収益の厳選を確認する作業を実施するなどの発展が考えられます。
4.6. 適時開示情報を使用して特別損失銘柄を除外
strategy_idの4/5/6にtdnet.csv.gzを使用して特別損失を発表した銘柄を除外する戦略を実装しています。strategy_idに4/5/6を指定してバックテストを実施し、設定した仮説(特別損失開示による株価の下落を回避し、ポートフォリオの利益を向上できるとの仮説)が有効なのかどうかを検証します。
特別損失を発表した銘柄を除外してポートフォリオを組成します。
# 戦略毎に処理
for strategy_id in tqdm([4, 5, 6]):
# ポートフォリオ組成
str_ret = ScoringService.predict(inputs, start_dt=start_dt, strategy_id=strategy_id)
# ポートフォリオを保存
with open(f"chapter03-tutorial-02-backtest-{strategy_id}.csv", mode="w") as f:
f.write(str_ret)バックテストを実行します。
# 戦略毎に処理
for strategy_id in tqdm([4, 5, 6]):
# ポートフォリオを読み込み
df_submit = Backtest.load_submit(f"chapter03-tutorial-02-backtest-{strategy_id}.csv")
# バックテスト実行
results[strategy_id], stocks[strategy_id] = Backtest.run(df_submit.loc[start_dt:], backtest_codes, backtest_price)4.6.1. 改善を試みたバックテスト結果の考察
ここではまずweek_returnの累積をプロットして効果が出ているかを確認します。
# 描画領域を定義
fig, axes = plt.subplots(1, 1, figsize=(20, 8), sharex=True, sharey=True)
# 戦略毎に処理
for k in results.keys():
# 描画位置を指定
ax = axes
# 戦略別の累積リターンを描画
results[k].set_index("date").loc[:, ["week_return"]].rename(
columns={"week_return": f"{k}: week_return"}
).cumsum().plot(ax=ax)
# ユニバースの週次リターンの累積をプロット
df_universe_return.cumsum().plot(ax=ax, color="black", label="universe")
# 表示を調整
ax.set_title("Cumulative week_return")
# グリッドを表示
ax.grid(True)
# 描画
plt.show()
2及び5の戦略に注目すると、特別損失を発表した銘柄を除外するとポートフォリオの利益が上昇することもあることがわかります。ここでは、勝率やシャープレシオ等これまで実施してきた詳細な分析については実施していませんが、実際の戦略の決定には一つの評価指標のみを使用するのではなく、複数の評価指標を使用して総合的に判断することが重要です。前述の評価方法などを参考に各自で実施してみてください。
また、今回は適時開示情報の特別損失のみを使用していますが、それ以外にも株価に影響を与える開示項目があるかもしれません、上記のように仮説を立てて一つずつ効果を比較しながら検証することが重要になります。
4.6.2. バックテストの総括
まず、1及び2の戦略はユニバースと比較して高い収益性を実現できていました。最高値モデルと最安値モデルを足し合わせた1の戦略が、より安定的な収益を上げることを期待していましたが、シャープレシオなどを比較しても2の戦略の方が優れているため、最高値モデルと最安値モデルを足すよりも、現時点では最高値モデルを単体で利用するほうが良い結果が期待できそうです。
ただし、最高値モデルと最安値モデルの組み合わせ方が悪かった可能性もあります。というのも、2章で作成した予測モデルはあくまでスピアマンの順位相関を意識して作られたため、予測値の幅よりも順位を当てることを意識して設計されています。この場合、予測の幅が必ずしも実際の幅と一致する必要はありませんので、単純に足すよりもscikit-learnライブラリのStandardScaler( https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html )による標準化などを通して、一旦正規化を実施してから足すのがよいのではないかと考えられます。
このようにモデルの構築と利用方法の組み合わせによって銘柄選択の戦略は決まりますので、是非様々な試行錯誤を実施してください。
4.7. 投稿用パッケージの作成
4.7.1. 投稿用パッケージのディレクトリの作成
ここまで、モデルの作成及び評価をしてきました。ここからは、投稿用のパッケージを作成します。ランタイム環境用のモデルは以下の構成である必要がありますので、まずは必要なディレクトリを作成していきます。また、適宜「3.8. 投稿用パッケージの作成」についてもご参照ください。
.
├── model 必須 学習済モデルを置くディレクトリ
│ └── ...
├── src 必須 Python のプログラムを置くディレクトリ
│ ├── predictor.py 必須 最初のプログラムが呼び出すファイル
│ └── ... その他のファイル (ディレクトリ作成可能)
└── requirements.txt 任意4.7.2. ライブラリバージョン調整
本章で利用したモジュールのバージョンを調整するために、requirements.txtに以下を記載して保存します。
joblib==1.0.1
numpy==1.19.5
pandas==1.1.5
scikit-learn==0.20.3
scipy==1.2.1
seaborn==0.9.04.7.3. ランタイム実行用クラス及び提出ファイルの作成
最後に作成したScoringServiceクラスをpredictor.pyに書き込み、Zip形式で圧縮することで提出可能なzipファイルが作成されます。
Zipファイル作成例
$ ls
model requirements.txt src
$ zip -v submit.zip requirements.txt src/*.py model/*.pkl
updating: requirements.txt (in=0) (out=0) (stored 0%)
updating: src/predictor.py (in=11408) (out=2417) (deflated 79%)
updating: model/my_model_label_high_20.pkl . (in=18919345) (out=5071005) (deflated 73%)
updating: model/my_model_label_low_20.pkl . (in=18704305) (out=5006613) (deflated 73%)
total bytes=37635058, compressed=10080035 -> 73% savings5. ニュースデータから特徴量を抽出しよう
本章では、本コンペの大きな特徴であるニュースデータに注目し、ニュースデータから特徴量抽出を行う手法を紹介します。特徴量抽出を行うことでテキスト情報がスコア化されるため、予測モデルやポートフォリオに活用することが可能となります。
本章ではニュースデータから特徴量抽出を行う手法として、BERT(Bidirectional Encoder Representations from Transformers)を採用しています。BERTはGoogleによって開発された、自然言語処理(NLP)の事前学習のためのTransformerベースの機械学習手法であり(引用:Wikipedia: BERT (言語モデル))、近年様々な分野で高い性能を発揮しているニューラルネットを基盤とする言語モデルの一種です。
本チュートリアルでは、東北大学の乾・鈴木研究室が公開した訓練済み日本語BERTモデルを利用します(こちら)。なお、BERTモデルへの入力であるコーパス(言語の標本を抽出した集合。テキストの集合を示します)は、そのBERTモデルが学習された時と同様の前処理を行う必要があることに注意が必要です。
今回使用する"cl-tohoku/bert-base-japanese-whole-word-masking"モデルは、mecab-ipadic-NEologdによりトークナイズされ、その後Wordpiece subword encoderよりsubword化していますので、本チュートリアルでもその流れに沿った処理を実施しています。トークナイズとは、テキストを決めた基準のトークンに区切ることです(5.2に詳細記載)。他のBERTモデルを利用することも可能ですが、その場合は、そのBERTモデルの入力とするコーパスがどのように前処理が行われたかを確認し適切な前処理を実施するようにしてください。
また、本コンペティションでは、以下のように外部データの利用を制限しております。こちらも合わせてご確認ください。
・提供するデータ以外の外部データ(為替や金利データ等)や、提供するデータの期間外のヒストリカルデータを用いてモデルを学習することは禁止。(例として、2015年以前の株価等) ・ただし、言語資源の外部データについては、第三者の権利を侵害しない、無償で誰でも利用可能なオープンなものに限り利用可能。(例として、形態素解析辞書や、BERTモデル)
5.1. テキストからの特徴量抽出方法の紹介
テキストデータに内在する情報を特徴量として抽出する方法としては、単語の頻度ベース、単語の分散表現ベース、言語モデルベース等の方法が存在します。下記では、それぞれについていくつかの方法を紹介します。
単語の頻度ベース
-
テキストに登場する各単語の頻度を行列化した単語文書行列を用いる方法 (例)TF-IDF(Term Frequency–Inverse Document Frequency)
-
テキストの潜在意味を抽出するトピックモデリングの方法 (例)LSA(Latent Semantic Analysis), LDA(Latent Dirichlet Allocation)
これらの方法は、単語の頻度行列の使用を基盤としているため、コーパス内に単語が増えれば増えるほど高い計算リソースが要求されます。
モデリング名 |
説明 |
引用 |
LSA(Latent Semantic Analysis) |
LSAはベクトル空間モデルを利用した自然言語処理の技法の1つで、文書群とそこに含まれる用語群について、それらに関連した概念の集合を生成することで、その関係を分析する技術である。 |
|
LDA(Latent Dirichlet Allocation) |
LDAは文章中の潜在的なトピックを推定し、文章分類や、文章ベクトルの次元削減等に用いられる技術です。 |
単語の分散表現ベース
単語の分散表現(あるいは単語埋め込み)とは、単語を高次元の実数ベクトルで表現する技術です(引用:岩波データサイエンス: 分散表現(単語埋め込み))。次に挙げる方法は、単語を分散表現化する方法の一部です。
| 手法 | 説明 | 論文例 |
|---|---|---|
Word2Vec(CBOW) |
中心単語から周辺単語を予測し、前後単語との関係性を用いて分散表現を構築 |
|
Glove |
単語の頻度ベースのLSAと単語の分散表現ベースのWord2Vecを用いて分散表現を構築 |
|
FastText |
単語をSubword化することで、Out-Of-Vocabularyに頑健な分散表現を構築 |
|
Elmo |
RNNベースの言語モデルであるbiLMを用いて、文脈を反映する分散表現を構築 |
言語モデルベース(ニューラルネット基盤の言語モデルのみを説明)
-
RNN基盤(LSTM, GRU, LMを含む)の内部状態を特徴量として抽出
-
Transformer(BERT等Attention機構を用いたモデルを含む)基盤の内部状態を特徴量として抽出
これらの方法は、膨大なパラメータを持つモデルを膨大なデータを用いて学習させるため、テキストデータについてより高次元の潜在表現を学習できることが知られています。また、このようなモデルから抽出した特徴量は多様なタスクにおいて適用でき、高いパフォーマンスを表すことが知られています。
本チュートリアルでは、上記観点からも最も汎用性が高いと思われるBERTモデルを利用した特徴量抽出に取り組みます。
5.2. 実行環境
本チュートリアルでは、CPUとGPUどちらの環境でも実行可能なモデルを使用しています。しかし、本チュートリアルで紹介するBERTの特徴量抽出の処理は、CPU環境ではかなりの時間がかかります。そのため、GPU環境をお持ちでない方は、多少の制限はあるものの実行環境として無料でGPU環境が使えるGoogle Colaboratoryを利用することを強くお勧めします。また、本章を実行しなくても問題なく特徴量をご利用いただけるように、本章で抽出したBERT特徴量はpklファイルとして こちら でも提供しています。
5.2.1. Google Colaboratoryの環境設定
本コンペの5章、6章のチュートリアルをGoogle Colaboratory上で動かすためには、まず以下の手順でGoogle Drive上にファイルを設置します。
-
Google DriveのMy Driveに
JPX_competitionというフォルダーを作成します。 -
1で作成した
JPX_competitionフォルダーにデータを保存するためのdata_dir_comp2フォルダーを作成します。 -
SIGNATEのコンペティションサイトよりダウンロードした各種データを2で作成した
data_dir_comp2フォルダーにアップロードします。
次にGoogle Colaboratory上でチュートリアルのnotebookを展開します。本チュートリアルのnotebookはGoogle Colaboratory上でも実行可能となっております。各章のnotebookは以下のそれぞれのリンク先を開き、開いたページでRawを右クリックし、「リンク先を名前をつけて保存」を選択することでダウンロード可能です。
以下、5章を例にGoogle Colaboratoryでチュートリアルのnoteboookを使用する方法を説明します。
-
Google Drive の My Drive 内に作成した
JPX_competitionフォルダーに3章用のnotebookを保存するためのChapter05フォルダーを作成します。 -
上記のリンク先から5章のnotebookをダウンロードして、先程作成した
Chapter05フォルダーに20210226_chapter05_tutorial.ipynというファイル名で保存してください。 -
Google Driveにアップロードした
20210226_chapter05_tutorial.ipynbファイルをダブルクリックして Google Colaboratory で開きます。 -
Google Colaboratoryの環境で本チュートリアルを実行する場合、最初に以下のコードを実行して Google Colaboratory 上の notebook から Google Drive にアクセスできるようにしてください。
# Google Colab環境ではGoogle Driveをマウントしてアクセスできるようにします。
import sys
if 'google.colab' in sys.modules:
# Google Drive をマウントします
from google.colab import drive
mount_dir = "/content/drive"
drive.mount(mount_dir)5.2.2. 必要なライブラリのインストール
本チュートリアル内では、上記の実行環境には含まれていないライブラリを使用するため、以下のコマンドを使用して個別にインストールします。Notebookに記載がある通り、Google Colaboratory上においても実行できます。
# テキスト解析用にmecabをインストールします。
# 日本語表記を含む可視化のため、フォントもインストールしています。
apt-get update
apt-get install -y build-essential sudo mecab libmecab-dev mecab-ipadic-utf8 fonts-ipafont-gothic file
# 必要なライブラリをインストールします。
pip install --no-cache-dir pandas==1.1.5 numpy==1.19.5 scattertext==0.1.0.0 wordcloud==1.8.1 torch==1.7.1 torchvision==0.8.2 transformers==4.2.2 mecab-python3==0.996.6rc1 ipadic==1.0.0 neologdn==0.4 fugashi==1.0.5 japanize-matplotlib==1.1.3 gensim==3.8.3 pyLDAvis==2.1.2
# mecab用のipadic-neologd辞書をインストールします。
# ipadic-neologd辞書は非常に頻繁に更新されるため、同様の解析結果が得られるようにバージョンを指定します。そのため、git clone時にバージョン(--branch v0.0.7 --single-branch)を指定します。
# git cloneよりインストールファイルが入っているレポジトリをローカル環境に落とします。
git clone https://github.com/neologd/mecab-ipadic-neologd.git --branch v0.0.7 --single-branch
# インストールの途中、yesのコマンドを叩かないとインストールが実行されません。yesコマンドを使うことで、渡された引数を常に叩くようになります。
yes yes | mecab-ipadic-neologd/bin/install-mecab-ipadic-neologd5.2.3. ライブラリの読み込み
本チュートリアルで利用するライブラリを読み込みます。
# 基本ライブラリ
import re
import os
import sys
import math
import random
import json
import joblib
import numpy as np
import pandas as pd
from scipy import stats
import string
from copy import copy
from glob import glob
from itertools import chain
import gc
# テキスト解析関連
import MeCab
import unicodedata
import neologdn
# 可視化関連
from tqdm.auto import tqdm
from IPython.display import display, display_markdown, IFrame
import scattertext as st
from wordcloud import WordCloud
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
import gensim
import pyLDAvis
import pyLDAvis.gensim
#PCA関連
from sklearn.decomposition import PCA, KernelPCA
# ニューラルネット関連
import torch
from torch import nn
import torch.nn.functional as F
import transformers
from transformers import BertJapaneseTokenizer
from torch.utils.data import DataLoader, Dataset as _Dataset
# notebook上でpyLDAvisより可視化を行う場合の設定
pyLDAvis.enable_notebook()5.2.4. ライブラリ解説
| ライブラリ名 | 目的 | 公式ドキュメント | 入門解説 |
|---|---|---|---|
re |
データの処理 |
||
numpy |
データの処理 |
||
pandas |
データの処理 |
||
scipy |
統計用のライブラリ |
||
glob |
ファイルの検知 |
||
MeCab |
テキスト解析 |
MeCab: Yet Another Part-of-Speech and Morphological Analyzer |
|
unicodedata |
unicode正規化 |
||
neologdn |
テキスト正規化 |
||
tqdm |
計算の進捗確認 |
||
IPython.display |
データ可視化 |
||
scattertext |
コーパス可視化 |
||
wordcloud |
コーパス可視化 |
||
matplotlib |
データの可視化 |
||
japanize_matplotlib |
データの可視化 |
||
seaborn |
データの可視化 |
||
gensim |
コーパス解析 |
||
pyLDAvis |
コーパス可視化 |
||
torch |
ニューラルネットモデリング |
Qiita:PyTorch入門 [公式Tutorial:DEEP LEARNING WITH PYTORCH: A 60 MINUTE BLITZを読む] |
|
transformers |
事前学習言語処理モデル利用 |
5.2.5. notebook環境の構築
ファイルパスの設定
notebook実行時に使用するファイルパスを設定します。
# colab環境で実行する場合
if 'google.colab' in sys.modules:
CONFIG = {
'base_path': f'{mount_dir}/MyDrive/JPX_competition/workspace',
'article_path': f'{mount_dir}/MyDrive/JPX_competition/data_dir_comp2/nikkei_article.csv.gz',
'stock_price_path': f'{mount_dir}/MyDrive/JPX_competition/data_dir_comp2/stock_price.csv.gz',
'stock_list_path': f'{mount_dir}/MyDrive/JPX_competition/data_dir_comp2/stock_list.csv.gz',
'dict_path': '/usr/lib/x86_64-linux-gnu/mecab/dic/mecab-ipadic-neologd',
'font_path': '/usr/share/fonts/truetype/fonts-japanese-gothic.ttf',
}
else:
CONFIG = {
'base_path': '/notebook/workspace',
'article_path': '/notebook/data_dir_comp2/nikkei_article.csv.gz',
'stock_price_path': '/notebook/data_dir_comp2/stock_price.csv.gz',
'stock_list_path': '/notebook/data_dir_comp2/stock_list.csv.gz',
'dict_path': '/usr/lib/x86_64-linux-gnu/mecab/dic/mecab-ipadic-neologd',
'font_path': '/usr/share/fonts/truetype/fonts-japanese-gothic.ttf',
}ディレクトリ作成
アウトプットされた実行結果ファイルを保存するためのディレクトリを作成しておきます。
for store_dir in ['headline_features', 'keywords_features', 'visualizations']:
os.makedirs(os.path.join(CONFIG["base_path"], store_dir), exist_ok=True)5.3. テキスト解析について
5.3.1. 形態素解析・トークナイズ
自然言語処理において、コーパスが前処理されていない状態である場合、該当するデータを使用するに当たって用途に合わせたトークナイズを行います。トークンとは意味を持つ文字列であり、主に、単語や単語より小さい単位を持つ形態素というものが該当します。また、テキストデータを予め決めた基準のトークンに区切ることをトークナイズと言います。英語においては、スペースを単語と単語の区切りとみなすことでトークナイズは簡単に行えます。また、句読点を用いることで文章と文章を区切ることもできます。
しかし、英語と異なり日本語はスペースや句読点だけでトークナイズを行うことは困難ですが、pythonではMeCabというライブラリを用いることで、日本語におけるトークナイズ処理を簡単に行うことができます。MeCabの動作原理に関して興味がある方は こちら をご参照ください。
5.3.2. テキスト解析に用いるtaggerの構築
MeCabでトークナイズを行うクラス(トークナイザ)をtaggerと呼びます。MeCabのtaggerを構築する時は、その出力形式をオプションとして渡すことができます。オプションには、以下の4つがあります。
-
-Ochasen:ChaSen互換形式
-
-Owakati:分かち書きのみを出力
-
-Oyomi:読みのみ(振り仮名)を出力
-
-Odump:単語の全情報を出力
その中でも、OwakatiとOchasenの2つがよく使用されています。Owakatiはテキストをトークナイズし、空白でテキストをトークン単位に区切ります。Ochasenはトークナイズを行うと共に、トークンの品詞情報や原型、活用型などを共に返します。以降の解析では、これらのtaggerを使用しますので、各々のtaggerに出力形式オプションを引数として設定しています。
owakati = MeCab.Tagger(f"-Owakati -d {CONFIG['dict_path']}")
ochasen = MeCab.Tagger(f"-Ochasen -d {CONFIG['dict_path']}")
# taggerのparseを使うことで、各々の機能を確認することができます。
text = 'taggerの役割を確認してみます。'
print('owakati:\n' + owakati.parse(text))
print('ochasen:\n' + ochasen.parse(text))出力結果は以下の通りです。テキストのトークナイズ、品詞情報の取得に成功していることが確認できます。
owakati:
tagger の 役割 を 確認 し て み ます 。
ochasen:
tagger タガー tagger 名詞-固有名詞-一般
の ノ の 助詞-連体化
役割 ヤクワリ 役割 名詞-一般
を ヲ を 助詞-格助詞-一般
確認 カクニン 確認 名詞-サ変接続
し シ する 動詞-自立 サ変・スル 連用形
て テ て 助詞-接続助詞
み ミ みる 動詞-非自立 一段 連用形
ます マス ます 助動詞 特殊・マス 基本形
。 。 。 記号-句点
EOS5.3.3. 本番提出用のクラス作成方法について
本章で構築するモデルは記述がとても長いため、3章及び4章のように最後に一気にモデル提出用のクラスを作成するのではなく、以下のように段階的にモデル提出用のクラスを作成していきます。まずは、ベースとなる基底クラス SentimentGenerator を定義しています。
class SentimentGenerator(object):
# 各々の変数に関しては、後述のチュートリアル内で説明します。
article_columns = None
punctuation_replace_dict = None
punctuation_remove_list = None
device = None
feature_extractor = None
headline_feature_combiner_handler = None
keywords_feature_combiner_handler = None5.4. ニュースデータ処理の流れ
本チュートリアルでは、5章及び6章でニュースデータを以下のように処理していきます。
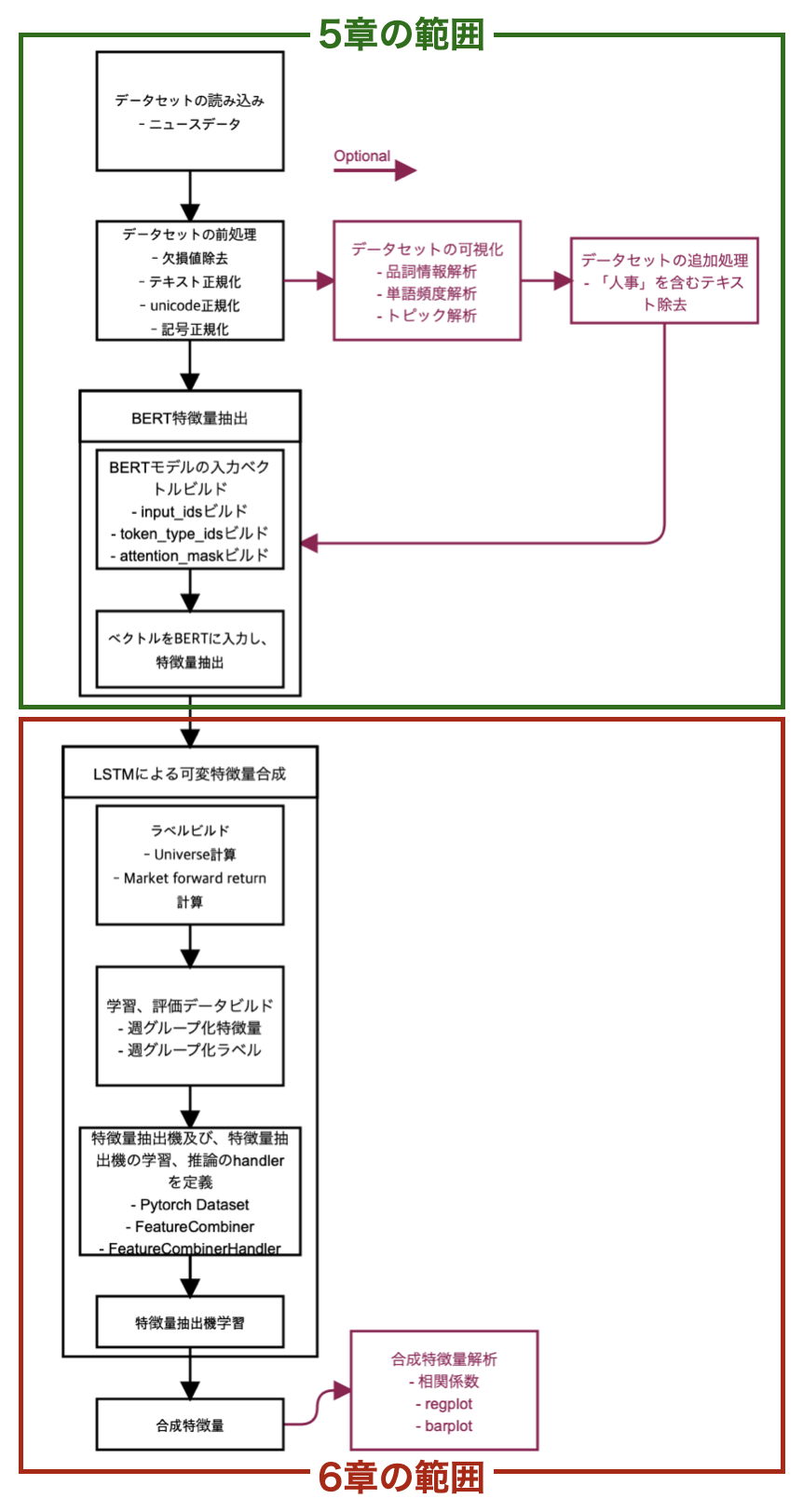
5.5. 利用するテキストデータについて
本節では、使用するテキストデータについてのデータの読み込みや内容について概観します。
5.5.1. テキストデータの読み込み
本チュートリアルで用いるテキストデータを読み込み、確認します。
articles = pd.read_csv(CONFIG['article_path'])
display(articles.head(3))5.5.2. テキストデータの内容を概観
テキストデータの構成を把握するため、各columnのユニークなデータの件数やデータの形等を確認します。読み込んだデータに関して細かくそのデータ数や形式を確認する作業はデータの理解を助けます。
# key: column, value: 重複を排除したデータ件数のdict型宣言
n_unique = {}
for column in articles.columns:
# column毎の重複を排除したデータ件数をn_uniqueに追加する。
n_unique[column] = len(articles[column].unique())
display_markdown('Number of unique data', raw=True)
# n_uniqueをpd.Series形式に変換する。articles.dtypesよりcolumnごとのdtypeを取得
# これらをpd.concatによってテーブル形式に変換し、表示
display(pd.concat([pd.Series(n_unique).rename('n_unique'), articles.dtypes.rename('dtype')], axis=1))出力結果は以下の通りです。
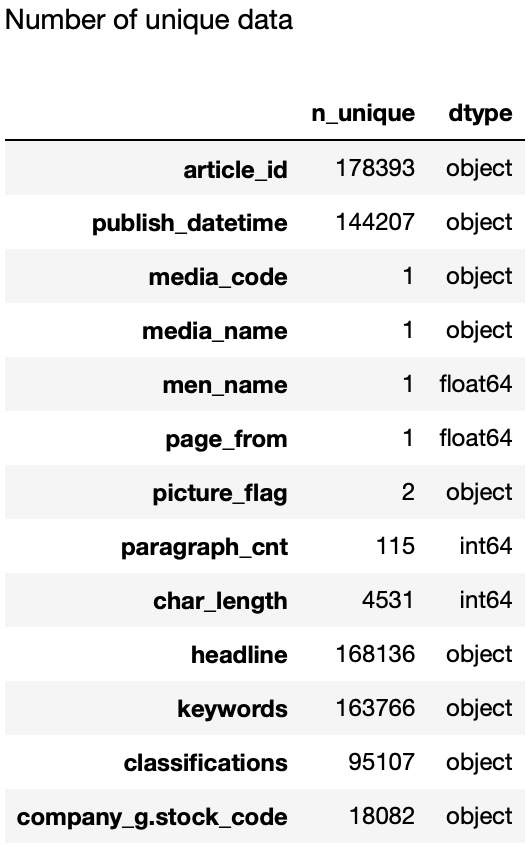
テキストを解析する際、そのテキストが持つ意味を考慮するためには、テキストを単なる文字列の集合と見なすのではなく、より踏み込んだ前処理が必要となります。そのため、テキストを単なる文字コード(intの離散値)の集合と見做し、これを数値的な特徴量として用いたとしても、テキストの意味的な解析は不可能です。このような場合、文字列長の分布や各漢字の出現頻度といった表層的な解析しかできなくなると推察されます。そのため、本チュートリアルでは、テキスト解析には別途の前処理を実行し、モデリングに適した特徴量を抽出します。(詳細は5.7.6節にて説明)
各columnを見ると、テキストの単純なid番号を含む`article_id` と時刻情報を含む`publish_datetime` を除けば、データセット内で利用できそうなデータは headline, keywords, classifications, company_g.stock_code になりそうです。以下にこれらのデータサンプルを表示します。
# 表示するcolumnを定義する。
columns = ['headline', 'keywords', 'classifications', 'company_g.stock_code']
for column in columns:
display_markdown(f'#### {column}', raw=True)
# 欠損値が含まれることがあるため、どちらかに欠損値が存在するデータを除去する。
# 同様のindexを持つ5個のサンプルデータを表示。
display(articles[columns].dropna()[column].head(5))出力結果は以下のとおりです。
headline
10 ゴーン元会長、周到な不意打ち出国 司法批判の声明
19 地銀が変わる、始まったマニュアルなき大競争
20 JXTG・国際帝石、UAE新取引所に出資へ
22 元日付のこういうコラムは、ふつうなら来し方行く末に思いをはせ、まずは新年をことほぐものである...
26 Googleの最新AI、読解力も人間超え 驚異の学習法\n超人間・万能AI(上)
Name: headline, dtype: object
keywords
10 カルロス・ゴーン\n日産自動車\nグレッグ・ケリー\n弘中惇一郎\nMusicTelevis...
19 金融検査マニュアル\nマニュアル\n笹原晶博\n安田光春\n金融機関\n銀行\n地方銀行\n...
20 国際石油開発帝石\nICEフューチャーズ・アブダビ\nJXTGホールディングス\nアラブ首長...
22 春秋\nカルロス・ゴーン\nコラム\n来し方行く末\n思い\n日付\n新年
26 中田敦\nストックマーク\nグーグル\nBERT\nAI\nNII\nロボット\n言語モデル...
Name: keywords, dtype: object
classifications
10 $絵写表記事\nT7201\nPD271\nN0001351\nN0044371\n#W50...
19 $絵写表記事\nT8524\nPD473\nN0070017\nN0070087\n#W20...
20 $絵写表記事\nT1605\nT5020\nPD372\nPD111\nN0031217\n...
22 「春秋」\n*春秋\nT7201\nPD271\nN0001351\n#W50305\n#W...
26 $絵写表記事\nT9432\nPD651\nN0015006
Name: classifications, dtype: object
company_g.stock_code
10 7201
19 8524
20 1605\n5020
22 7201
26 9432
Name: company_g.stock_code, dtype: object本チュートリアルでは、ニュースのデータセットを用いて、そのニュースがマーケットに対して持っている潜在表現を特徴量として取得することを目的としています。
上記で表示したcolumnごとのサンプルを見ると、`headline` のデータはニュースの要約内容であり、この中から潜在表現を抽出できそうです。また、`keywords` もニュースが持つ特性がキーワード化されたものであり、この中からも潜在表現を抽出できそうです。一方で、`classifications` は`keywords` と同様に、ニュースがもつ特性を表していますが、このままの状態では扱いにくく、`keywords` と重複する情報であるため、解析からは省きます。また、ニュースと株式銘柄を紐付ける`company_g.stock_code` は有力そうな情報ではありますが、あくまで数値でありテキスト解析の観点では適していません。よって、`headline` と`keywords` 及びニュースが公開された時刻を表す`publish_datetime` を保持し、他のデータは以下の手順で取り除いておきます。
articles = articles[['publish_datetime', 'headline', 'keywords']]
# ニュース時刻をindexとしてセット
articles = articles.set_index('publish_datetime')
# str形式のdatetimeをpd.Timestamp形式に変換
articles.index = pd.to_datetime(articles.index)5.5.3. 本番提出用のクラスへ組み込み
ここまでの処理をload_articles関数として SentimentGenerator クラスに追加します。
# 生データから使用するコラムを設定する
SentimentGenerator.article_columns = ['publish_datetime', 'headline', 'keywords']
# 上記のコードを用いて、本番提出用のクラスにclassmethodを追加
@classmethod
def load_articles(cls, path, start_dt=None, end_dt=None):
# csvをロードする
# headline、keywordsをcolumnとして使用。publish_datetimeをindexとして使用。
articles = pd.read_csv(path)[cls.article_columns].set_index('publish_datetime')
# str形式のdatetimeをpd.Timestamp形式に変換
articles.index = pd.to_datetime(articles.index)
# 必要な場合、使用するデータの範囲を指定する
return articles[start_dt:end_dt]
# SentimentGeneratorに定義したclassmethodを追加する
SentimentGenerator.load_articles = load_articles
# SentimentGenerator使用する全体流れを記述
articles = SentimentGenerator.load_articles(path=CONFIG["article_path"])5.6. データセットの前処理
多用な文字、記号が存在する日本語のテキスト解析において、データセットの前処理は非常に重要な処理です。例えば、日本語のテキストは、半角文字と全角文字が混在して使われる場合があります。同じテキスト内であっても、同じ単語が半角文字と全角文字で混在して使われる場合、人はそれらが単語が同じであることを認識できますが、モデルにおいては、異なる別の単語として認識されてしまいます。
さらに、半角文字と全角文字が混在する単語が、学習時に観察していない単語(未知語, Out-of-Vocabulary等)である場合には、その意味は失われてしまい、結果としてテキスト全体の意味が崩れる可能性もあります。このような問題を防止するため、データセットの前処理として 「テキストデータの正規化」 が用いられます。
本節では、使用するテキストデータがどのよう文字や記号で構成されていて、どのような期待していない文字や記号などを含んでいるかを確認します。更に、それらの期待していない情報に対して、置換処理や除去処理を実施する正規化方法を説明します。
また、前処理の一つとして欠損値に対する処理があります。欠損値の確認は、そのデータを理解するための基本的な作業です。連続する数値データにおいて欠損値が存在する場合は補正や補完を行うことも可能ですが、ニュースデータは各々の記事が連続せず、独立した内容を含んでいることから、このような方法は適していません。本チュートリアルではheadline及びkeywords両方の特徴量を同時に用いるため、どちらか片方に欠損値が存在する場合は利用しないデータとみなし除去しています。
5.6.1. 欠損値除去
まずは、欠損値があるかを確認します。確認する手順は以下の通りです。
articles.isnull().any()出力結果は以下の通りです。
headline False
keywords True
dtype: boolどちらかに欠損値がある場合、そのデータを除去する処理を行います。
# 欠損値を取り除く
articles = articles.dropna()
articles.isnull().any()出力結果は以下の通りです。欠損値が除去されていることがわかります。
headline False
keywords False
dtype: bool5.6.2. テキストデータの正規化
次に、本節で行うテキストデータの正規化についての概略を記載しています。それぞれ以下のとおり neologdn正規化、unicode正規化、マニュアル処理の3つに分けています。
neologdn正規化
正規化前 |
正規化後 |
全角英字 |
半角英字 |
全角数字 |
半角数字 |
全角スペース |
半角スペース |
複数回スペース |
単一スペース |
正しくないスペース |
除去 |
半角カナ |
全角カナ |
複数回長音記号 |
単一長音記号 |
一部全角記号 |
半角記号 |
一部半角記号 |
全角記号 |
unicode正規化
正規化前 |
正規化後 |
丸囲みの数字 |
数字 |
ローマ数字 |
アルファベット形式 |
単位 |
アルファベットや日本語形式 |
省略文字 |
記号及び日本語形式 |
マニュアル処理
正規化前 |
正規化後 |
一部第一水準、第二水準漢字 |
JISx0208に存在する漢字(Wikipedia: JIS X 0208) |
一部不必要な記号 |
除去 |
一部乱用記号 |
置換 |
neologdn正規化及び、unicode正規化に関しては、実際のコードでは上記で記入していないパターンに関しても正規化を行っています。それぞれの詳細や関連リンクは後述します。
5.6.3. 全角文字の確認
まずは全角スペース、全角アルファベット、全角数字が含まれているかを確認します。なお、"\u3000"は全角スペース、r"[A-Za-z]"は全角アルファベットの正規表現、r"[0-9]は全角数字の正規表現を表します。
for column in articles.columns:
for check_target in ["\u3000", r"[A-Za-z]", r"[0-9]"]:
display(f'Coulmn: {column}, Contains {check_target}: {articles[column].str.contains(check_target).any()}')出力結果は以下の通りです。
'Coulmn: headline, Contains \u3000: True'
'Coulmn: headline, Contains [A-Za-z]: True'
'Coulmn: headline, Contains [0-9]: True'
'Coulmn: keywords, Contains \u3000: True'
'Coulmn: keywords, Contains [A-Za-z]: True'
'Coulmn: keywords, Contains [0-9]: True'全角スペース、全角アルファベット、全角数字全てがテキストデータのコーパス内に含まれていることがわかります。それぞれの文字・記号を含む例を出力してみます。
全角スペースを持つケース
display(articles['headline'][articles['headline'].str.contains('\u3000')][0])
display(articles['keywords'][articles['keywords'].str.contains('\u3000')][0])出力結果は以下の通りです。
'日米貿易協定が発効\u3000TPP土台に自由貿易圏拡大\n日本、RCEPに波及期待'
'米ツアー\u3000ズームアップ\nアダム・スコット\nグレッグ・ノーマン\nコリン・モリカワ\nコリン・モンゴメリー\nゴルファー\nゴルフジャーナリスト\nジム・マッケイブ\nジャスティン・ローズ\nスティーブ・エルキントン\nスティーブ・ジョーンズ\nスティーブ・ストリッカー\nセルヒオ・ガルシア\nタイガー・ウッズ\nダスティン・ジョンソン\nデービス・ラブ3世\nトム・リーマン\nトム・ワトソン\nニック・ファルド\nバッバ・ワトソン\nビクトル・ホブラン\nビジェイ・シン\nフィル・ミケルソン\nフレッド・カプルス\nブラッド・ファクソン\nベルンハルト・ランガー\nポール・ケーシー\nマシュー・ウォルフ\nマスターズ・トーナメント\nマット・クーチャー\nマーク・オメーラ\nマーク・マクナルティ\n世界トップ\n主流\n尾崎将司'全角アルファベットを持つケース
display(articles['headline'][articles['headline'].str.contains(r"[A-Za-z]")][0])
display(articles['keywords'][articles['keywords'].str.contains(r"[A-Za-z]")][0])出力結果は以下の通りです。
'JXTG・国際帝石、UAE新取引所に出資へ'
'政府\n米国政府\n東アジア地域包括的経済連携\nTPP\n安倍晋三\n貿易協定\n自由貿易\n貿易\n関税\n発効\n日米\n撤廃\n波及\n双方'全角数字を持つケース
display(articles['headline'][articles['headline'].str.contains(r"[0-9]")][0])
display(articles['keywords'][articles['keywords'].str.contains(r"[0-9]")][0])出力結果は以下の通りです。
'「雇用制度全般の見直しを」中西経団連会長\n経済3団体トップの年頭所感'
'政府統計\nダウ\n小幅高\nダウ工業株30種平均\n貿易協議\n株式市場\n米中\n米国株\n進展'5.6.4. neologdnを用いたテキストの正規化の挙動確認
ここでは、neologdnを用いて、先程確認した全角アルファベットや全角数字、また、その他の半角カタカナや一部の全角記号等に対して正規化を行います。neologdnの正規化規則に関して詳しい情報が必要な場合は こちら を参照して下さい。
neologdnを用いたテキスト正規化の挙動を確認するため、以下のサンプルテキストを用意しています。
text = '全角アルファベット:A, 全角数字:0, 全角スペース: , 半角カナ:ア'
# 正規化前のテキストを確認
display(text)正規化前の出力結果は以下の通りです。
'全角アルファベット:A, 全角数字:0, 全角スペース:\u3000, 半角カナ:ア'neologdn.normalize関数を用いてよりテキストの正規化を行います。
# 正規化後を確認
display(neologdn.normalize(text))出力結果は以下の通りです。全角アルファベットが半角アルファベットに、全角数字が半角数字に、全角スペースが半角スペースに、半角カタカナが全角カタカナになったことが確認できます。
'全角アルファベット:A,全角数字:0,全角スペース: ,半角カナ:ア'5.6.5. neologdnを用いたテキストの正規化
neologdnの挙動が確認できましたので、neologdnを用いて本チュートリアルで用いるテキストデータ全体について正規化します。なお、正規化にあたって一つ注意すべきところがあります。今回使用している`keywords` のデータは、名詞で構成されている単語が半角スペースで区切られています。この場合、neologdnの仕様により正規化を行うことで、半角スペースが全て除去されてしまい、各keywordsが一つの大きなkeywordsとなってしまい、MeCabによる正しいトークナイズが不可能となってしまいます。そのため、半角スペースの情報が失われないように、一度半角スペースを全て改行コードに書き換え、正規化した後に当該改行コードを半角スペースに再変換する処理を行うことで、半角スペースの情報を維持するように正規化を行っています。MeCabによるトークナイズの際には、半角スペースが残っている状態であっても、半角スペースの情報は除去されるため問題ありません。
for column in articles.columns:
articles[column] = articles[column].apply(lambda x: '\n'.join(x.split()))
# neologdnを使って正規化を行う。
articles[column] = articles[column].apply(lambda x: neologdn.normalize(x))
# 改行をスペースに置換する。
articles[column] = articles[column].str.replace('\n', ' ')
# 変換後を確認する。
display(articles.head(5))5.6.6. 本番提出用のクラスへ組み込み
ここまでの処理をnormalize_articles関数として SentimentGenerator クラスに追加します。
# 上記のコードを用いて、本番提出用のクラスにclassmethodを追加
@classmethod
def normalize_articles(cls, articles):
articles = articles.copy()
# 欠損値を取り除く
articles = articles.dropna()
for column in articles.columns:
# スペース(全角スペースを含む)はneologdn正規化時に全て除去される。
# ここでは、スペースの情報が失われないように、スペースを全て改行に書き換え、正規化後スペースに再変換する。
articles[column] = articles[column].apply(lambda x: '\n'.join(x.split()))
# neologdnを使って正規化を行う。
articles[column] = articles[column].apply(lambda x: neologdn.normalize(x))
# 改行をスペースに置換する。
articles[column] = articles[column].str.replace('\n', ' ')
return articles
# SentimentGeneratorに定義したclassmethodを追加する
SentimentGenerator.normalize_articles = normalize_articles
# SentimentGenerator使用する全体流れを記述
articles = SentimentGenerator.load_articles(path=CONFIG["article_path"])
articles = SentimentGenerator.normalize_articles(articles)5.6.7. テキスト内の記号情報について
テキスト内で記号が使われる場合がありますが、希少な記号や正しくない記号の使い方は、モデルがテキストを理解する上でノイズとなります。本節では、コーパス全体に含まれる記号を取得し、それらの記号がどのように使われているかを確認します。また、意味が薄いと思われる希少な記号は取り除きます。
まず、記号の情報を取得するため、ochasenを用いてテキストから品詞情報を取得してみます。返り値は各々以下を表します。
-
表層形: 単語そのもの
-
発音: 単語の発音
-
原型: 同士であれば変化する前の原形, 他の品詞の場合は表層形と同様
-
形態素の品詞型: 形態素は言語学の用語で意味をもつ表現要素の最小単位であり、その形態素を文法的な働きごとに分けたもの
-
活用形: 単語が活用するときの形
-
活用型: 助動詞の活用をいくつかの型に分類したもの
def parse_by_ochasen(tagger, text):
# Ochasenでmecab-ipadic-neologdの辞書を使ったときの、返り値のデータ順は以下となる。
columns = ['表層形', '発音', '原型', '形態素の品詞型', '活用形', '活用型']
# Ochasenよりコーパスタグ付けを行う。
parsed = [item.split('\t') for item in tagger.parse(text).split("\n") if item not in ('EOS', '')]
return pd.DataFrame(parsed, columns=columns)
text = 'テストテキストです。「記号を探してみます!」'
parsed = parse_by_ochasen(tagger=ochasen, text=text)
display(parsed)出力結果は以下の通りとなります。形態素の品詞型における品詞情報を確認すると、記号が記号として正しく認識されていることがわかります。
次に、品詞情報が記号である全ての記号を取得します。注意すべき点としては、MeCabでは記号の一部を「サ変接続」と認識してしまうことがあります。事例: MeCabさんが記号を「サ変接続」と認識してしまう
今回の環境において、実際にこれらの挙動は確認できていませんが、念の為「サ変接続」の中で、「漢字、ひらがな、カタカナ、アルファベット」を含まないものを記号として扱うこととします。以下のコードを実行し取得した記号を変数`punctuation` として扱います。
# 記号として扱う品詞型を定義し、以下のflagに該当する品詞型を持つものだけを取得する。
flags = ["記号", "サ変接続"]
# ひらがな、カタカナ、漢字、アルファベットを含まない、記号を全て取得。
punctuation_candidate = parsed['表層形'][parsed['形態素の品詞型'].apply(lambda x: any([flag in x for flag in flags]))]
# r"[一-龯ぁ-んァ-ンA-Za-z々ゝゞヽヾヴヵヶ]は正規表現であり、「漢字、ひらがな、カタカナ、大文字アルファベット、小文字アルファベット、々ゝゞヽヾヴヵヶのいずれか」を表す。
# これらを含まないものを記号として扱う。
punctuations = punctuation_candidate[~punctuation_candidate.str.contains(r"[一-龯ぁ-んァ-ンA-Za-z々ゝゞヽヾヴヵヶ]")]
punctuations = set(punctuations)
display(punctuations)出力結果は以下の通りです。
{'!」', '。', '「'}複合記号から単一記号を抽出し、集合に追加します。
for punctuation in punctuations:
punctuations = punctuations | set(punctuation)
display(set(punctuations))出力結果は以下の通りです。
{'!', '!」', '。', '「', '」'}最終的に上記のコードをまとめ、コーパス全体から記号を取得する関数を作成し、記号を取得します。
def build_punctuations(tagger, texts, flags = ["記号", "サ変接続"]):
gc.collect()
# textsがpd.Seriesでない時に、pd.Seriesに変換
if isinstance(texts, pd.Series) is False:
texts = pd.Series(texts)
punctuations = set()
for text in tqdm(texts):
# Ochasenより単語の品詞情報を取得
parsed = parse_by_ochasen(tagger=tagger, text=text)
# ひらがな、カタカナ、漢字、アルファベットを含まない、記号を全て取得
punctuation_candidate = parsed['表層形'][parsed['形態素の品詞型'].apply(lambda x: any([flag in x.split('-') for flag in flags]))]
punctuation_candidate = punctuation_candidate[~punctuation_candidate.str.contains(r"[一-龯ぁ-んァ-ンA-Za-z々ゝゞヽヾヴヵヶ]")]
punctuations = punctuations | set(punctuation_candidate.tolist())
# 複合記号から単一記号を抽出
for punctuation in punctuations:
punctuations = punctuations | set(punctuation)
return punctuations
headline_punctuations = build_punctuations(tagger=ochasen, texts=articles['headline'])
keywords_punctuations = build_punctuations(tagger=ochasen, texts=articles['keywords'])記号を含むテキストの例を表示します。
# headlineから、これら記号を含むテキストを表示
for punctuation in sorted(headline_punctuations, key=lambda x: len(x)):
print(f"punctuation: {punctuation}\n", articles['headline'][articles['headline'].apply(lambda x: punctuation in x)][0], '\n')
# keywordsから、これら記号を含むテキストを表示
for punctuation in sorted(keywords_punctuations, key=lambda x: len(x)):
print(f"punctuation: {punctuation}\n", articles['keywords'][articles['keywords'].apply(lambda x: punctuation in x)][0], '\n')記号や漢字の中には、パソコンの種類や環境に依存し、異なる環境で表示させた場合に、文字化けや表示できなくなる可能性のある文字「機種依存文字」が含まれます。これらの機種依存文字の中で記号の多くは、unicode正規化ライブラリを用いることで正規化することができます。また、星や音符などのあまり意味を持たない記号は取り除きます。一部の括弧は、見栄えのため用いられているだけであるため置換します。
以下では、置換するターゲットと除去するターゲットを定義しています。機種依存文字の第一水準、第二水準漢字に関しては、その数が膨大であることから、名前などに多く使われる一部の漢字を以下で定義し、置換を行います(第一水準漢字・第二水準漢字は、日本語の情報処理を標準化する目的にJISが定めた定義であり、平仮名、片仮名、漢字などの日本語の文字コードを定義したものです)。置換する漢字のリストは、 コチラ から取得しています。
# 機種依存文字の第一水準、第二水準漢字に関しては一部の漢字を以下で定義し、置換を行う。
JISx0208_replace_dict = {
'髙': "高",
'﨑': "崎",
'濵': "浜",
'賴': "頼",
'瀨': "瀬",
'德': "徳",
'蓜': "配",
'昻': "昂",
'桒': "桑",
'栁': "柳",
'犾': "犹",
'琪': "棋",
'裵': "裴",
'魲': "鱸",
'羽': "羽",
'焏': "丞",
'祥': "祥",
'曻': "昇",
'敎': "教",
'澈': "徹",
'曺': "曹",
'黑': "黒",
'塚': "塚",
'閒': "間",
'彅': "薙",
'匤': "匡",
'冝': "宜",
'埇': "甬",
'鮏': "鮭",
'伹': "但",
'杦': "杉",
'罇': "樽",
'柀': "披",
'﨤': "返",
'寬': "寛",
'神': "神",
'福': "福",
'礼': "礼",
'贒': "賢",
'逸': "逸",
'隆': "隆",
'靑': "青",
'飯': "飯",
'飼': "飼",
'緖': "緒",
'埈': "峻",
}
# 取得したpunctuationの観察から、置換すべき記号のdictionaryを作成する。
punctuation_replace_dict = {
**JISx0208_replace_dict,
'《': '〈',
'》': '〉',
'『': '「',
'』': '」',
'“': '"',
'!!': '!',
'〔': '[',
'〕': ']',
'χ': 'x'
}
# 取得したpunctuationの観察から、あまり意味を持たない記号のリストを作成し、これらを下記のコードで取り除く。
punctuation_remove_list = ['|', '■', '◆', '●', '★', '☆', '♪', '〃', '△', '○', '□']置換するために定義した機種依存文字の第一水準、第二水準漢字がデータの中に含まれている確認します。
# 観測された漢字をstoreするためのsetを定義
catched_replace_targets = set()
for column in articles.columns:
display_markdown(f'column: {column}', raw=True)
# 定義した置換すべき漢字がデータに含まれているかをチェック
for key in JISx0208_replace_dict.keys():
# articles[column]にその漢字が含まれている場合、catched_replace_targetsに追加する。
if articles[column].str.contains(key).any():
catched_replace_targets.update(key)
# 観測された漢字のsetを表示する
display(catched_replace_targets)出力は以下となります。機種依存文字の第一水準、第二水準漢字がデータの中に含まれていることがわかります。
column: headline
{'塚', '彅', '曺', '礼', '神', '祥', '福', '羽', '逸', '隆', '飯', '飼'}
column: keywords
{'塚', '彅', '德', '曺', '礼', '神', '祥', '福', '羽', '逸', '隆', '飯', '飼', '髙', '﨑'}機種依存文字の丸囲みの数字、ローマ数字、単位、省略文字などは、unicodedataライブラリを用いたunicode正規化より置換を行います。正規化形式に関してはNFKC(Normalization Form Compatibility Composition)を用いています。
# unicodedata.normalize関数より、unicode正規化を行う。
text = '丸囲みの数字:①, ローマ数字:Ⅷ, 単位:㎜㍉, 省略文字:㈱'
unicodedata.normalize('NFKC', text)出力結果は以下の通りとなり、正規化が行われていることがわかります。
'丸囲みの数字:1, ローマ数字:VIII, 単位:mmミリ, 省略文字:(株)'コーパス全体のテキストから記号の置換及び除去を行います。
for column in articles.columns:
# punctuation_remove_listに含まれる記号を除去する
articles[column] = articles[column].str.replace(fr"[{''.join(punctuation_remove_list)}]", '')
# punctuation_replace_dictに含まれる記号を置換する
for replace_base, replace_target in punctuation_replace_dict.items():
articles[column] = articles[column].str.replace(replace_base, replace_target)
# unicode正規化を行う
articles[column] = articles[column].apply(lambda x: unicodedata.normalize('NFKC', x))
# 精製後確認
articles.head(10)5.6.8. 本番提出用のクラスへ組み込み
ここまでの処理をhandle_punctuations_in_articles関数として SentimentGenerator クラスに追加します。
# 作成した記号置換用のdictと記号削除用のリストをhandle_punctuations_in_articles関数内で使用するため、SentimentGeneratorに追加
SentimentGenerator.punctuation_remove_list = punctuation_remove_list
SentimentGenerator.punctuation_replace_dict = punctuation_replace_dict
# 上記のコードを用いて、本番提出用のクラスにclassmethodを追加
@classmethod
def handle_punctuations_in_articles(cls, articles):
articles = articles.copy()
for column in articles.columns:
# punctuation_remove_listに含まれる記号を除去する
articles[column] = articles[column].str.replace(fr"[{''.join(cls.punctuation_remove_list)}]", '')
# punctuation_replace_dictに含まれる記号を置換する
for replace_base, replace_target in cls.punctuation_replace_dict.items():
articles[column] = articles[column].str.replace(replace_base, replace_target)
# unicode正規化を行う
articles[column] = articles[column].apply(lambda x: unicodedata.normalize('NFKC', x))
return articles
# SentimentGeneratorに定義したclassmethodを追加する
SentimentGenerator.handle_punctuations_in_articles = handle_punctuations_in_articles
# SentimentGenerator使用する全体流れを記述
articles = SentimentGenerator.load_articles(path=CONFIG["article_path"])
articles = SentimentGenerator.normalize_articles(articles)
articles = SentimentGenerator.handle_punctuations_in_articles(articles)5.7. テキストデータの可視化
データセットの解析及び可視化は、データ自体の特性を理解する上で役に立つだけでなく、期待していない情報も含んでいるかどうかを確認する上でも役立ちます。本節では、扱うテキストデータががどのような特性を持っているのかを、品詞情報や単語の頻度により解析及び可視化し確認します。また、その結果に応じた前処理をデータセットに実施していきます。
5.7.1. 品詞情報取得
ここからの解析や可視化処理は品詞情報を必要とします。品詞情報の取得処理には時間がかかるため、あらかじめコーパス全体において品詞情報を取得します。
# コーパス全体をochasenによってparseする。
# メモリー節約のため、解析で使用する['表層形', '形態素の品詞型']の情報のみを残す。
parsed_headline_by_ochasen = articles['headline'].apply(lambda x: parse_by_ochasen(tagger=ochasen, text=x)[['表層形', '形態素の品詞型']])
parsed_keywords_by_ochasen = articles['keywords'].apply(lambda x: parse_by_ochasen(tagger=ochasen, text=x)[['表層形', '形態素の品詞型']])
# parseされたテキストデータを確認します。
display(parsed_headline_by_ochasen.head())
display(parsed_keywords_by_ochasen.head())出力結果は以下の通りです。
publish_datetime
2020-01-01 00:00:00+09:00 表層形 形態素の品詞型
0 日 名詞-固有名詞-地域-国
...
2020-01-01 00:00:00+09:00 表層形 形態素の品詞型
0 人事 名詞-一般
1 、 ...
2020-01-01 00:00:00+09:00 表層形 形態素の品詞型
0 人事 名詞-一般
1 、 ...
2020-01-01 00:00:00+09:00 表層形 形態素の品詞型
0 人事 名詞-一般
1 ...
2020-01-01 00:00:00+09:00 表層形 形態素の品詞型
0 「 記号-括弧...
Name: headline, dtype: object
publish_datetime
2020-01-01 00:00:00+09:00 表層形 形態素の品詞型
0 ...
2020-01-01 00:00:00+09:00 表層形 形態素の品詞型
0 衆議院 名詞-固有名詞-組織
2020-01-01 00:00:00+09:00 表層形 形態素の品詞型
0 外務省 名詞-固有名詞-組織
2020-01-01 00:00:00+09:00 表層形 形態素の品詞型
0 厚生労働省 名詞-固有名詞-組織
2020-01-01 00:00:00+09:00 表層形 形態素の品詞型
0 中西宏明 名詞...
Name: keywords, dtype: object5.7.2. 品詞情報解析
まずは、コーパス全体における品詞の分布を解析します。コーパス全体の品詞分布を調べる前に、単一テキストから品詞分布を取得してみましょう。
text = 'テストテキスト。コーパスの品詞情報を取得します。'
# 品詞情報を取得するため、ochasenを用いる
parsed = parse_by_ochasen(tagger=ochasen, text=text)
parsed['形態素の品詞型']出力結果は以下の通りです。
0 名詞-サ変接続
1 名詞-一般
2 記号-句点
3 名詞-一般
4 助詞-連体化
5 名詞-一般
6 名詞-一般
7 助詞-格助詞-一般
8 名詞-サ変接続
9 動詞-自立
10 助動詞
11 記号-句点
Name: 形態素の品詞型, dtype: object形態素の品詞型は、「名詞 サ変接続」などのように多重のクラスとして成り立っています。全体を掴むため、最上位の品詞型のみ(この場合名詞のみ)を取得するようにします。
word_classes = parsed['形態素の品詞型'].apply(lambda x: x.split('-')[0])
word_classes出力結果は以下の通りです。
0 名詞
1 名詞
2 記号
3 名詞
4 助詞
5 名詞
6 名詞
7 助詞
8 名詞
9 動詞
10 助動詞
11 記号
Name: 形態素の品詞型, dtype: object上で観察された品詞リストから、品詞ごとの数をカウントします。
word_classes.groupby(word_classes).count().to_dict()出力結果は以下の通りです。
{'助動詞': 1, '助詞': 2, '動詞': 1, '名詞': 6, '記号': 2}テキストごとに品詞の出現数を累積するため、出現数を品詞ごとにdict型で管理します。
count_of_word_classes = {}
# key: 品詞型, value: カウント数
for key, value in word_classes.groupby(word_classes).count().to_dict().items():
# 品詞が存在しない場合、新しく追加する。
if key not in count_of_word_classes:
count_of_word_classes[key] = value
# 品詞が存在する場合、既存のカウントに観察されたカウントを足す。
else:
count_of_word_classes[key] += value
# 確認する
count_of_word_classes出力結果は以下の通りです。
{'助動詞': 1, '助詞': 2, '動詞': 1, '名詞': 6, '記号': 2}上記で作成したコードをまとめて、コーパス全体から品詞情報を累積し取得する関数を作成しています。この関数は実行時間短縮のため、すでにochasenよりparseされた情報を入力としています。
def get_count_of_word_classes(parsed_by_ochasen):
gc.collect()
count_of_word_classes = {}
for parsed in tqdm(parsed_by_ochasen):
# 一番大きいくくりの品詞型だけを取得する。
word_classes = parsed['形態素の品詞型'].apply(lambda x: x.split('-')[0])
# 単一テキストの品詞カウントをdictionaryにアップデート
# key: 品詞型, value: カウント数
for key, value in word_classes.groupby(word_classes).count().to_dict().items():
# dictionaryに品詞が存在しない場合、新しく追加する。
if key not in count_of_word_classes:
count_of_word_classes[key] = value
# dictionaryに品詞が存在する場合、既存のカウントに観察されたカウントを足す。
else:
count_of_word_classes[key] += value
return pd.Series(count_of_word_classes).sort_values()
# headline, keywords各々のコーパスから品詞情報を取得する。
headline_count_of_word_classes = get_count_of_word_classes(parsed_by_ochasen=parsed_headline_by_ochasen)
keywords_count_of_word_classes = get_count_of_word_classes(parsed_by_ochasen=parsed_keywords_by_ochasen) それでは、2つのテキストデータ集合(headline 及び keywords )について品詞型の分布を比較してみましょう。2つのテキストデータの品詞ごとの累計をpd.concatを用いて重ね、一つのテーブルにしています。
count_of_word_classes_df = pd.concat([headline_count_of_word_classes.rename('headline'), keywords_count_of_word_classes.rename('keywords')], axis=1, sort=True)
# 確認する
count_of_word_classes_df出力結果は以下の通りです。
二つのテキストデータの品詞情報の分布を比較するため、それぞれのテキストデータ全体の単語数で各々を割り、品詞の割合情報を取得します。
normalized_count_of_word_classes_df = count_of_word_classes_df / count_of_word_classes_df.sum()
# 小数点6桁までで表示します。
display(normalized_count_of_word_classes_df.applymap('{:,.6f}'.format))出力結果は以下の通りです。
headline と keywords の品詞情報の分布から、それぞれの特性を理解することができます。まず、keywordsは、名詞の割合が高いことがわかります。keywordsの名前の通り、各ニュースに関連するトピックの名詞情報が含まれていると想定されますが、その他の品詞情報も含まれていることから、少からず文章構造に近いキーワードも入っていることが想定されます。
また、`headline` は、名詞以外にも助詞、動詞の割合も高く、テキストデータが文章構造を持っていると想定されます。また、正規化した上でも記号がかなり多く含まれているため、必要に応じてさらに記号に対する正規化や除去を行う必要があります。その際は、有意味な情報を持つ記号を除去しないように注意が必要です。
次に、上で表示したテーブルからさらに細かく品詞分布の違いを理解するため可視化してみます。品詞毎の出現数がかなり不均等であるため、そのような場合に有用なtruncated barplotを用いて可視化しています。
# 上下切断表示のため、縦二つのaxesを用意する。
fig, ax = plt.subplots(2, 1, sharex=True, figsize=(12, 5))
# 上下両方のaxesに同様のプロットを行う。
normalized_count_of_word_classes_df.sort_values('headline').plot(kind='bar', ax=ax[0])
normalized_count_of_word_classes_df.sort_values('headline').plot(kind='bar', ax=ax[1])
# 上下両方のy軸範囲を設定する。
ax[0].set_ylim((normalized_count_of_word_classes_df).max().max() - 0.9, 1)
ax[1].set_ylim(0, 0.03)
# 上のaxesでは、bottom部分表示(ticker, labelなど)、下のaxesでは、top部分表示を除去する。
ax[0].spines['bottom'].set_visible(False)
ax[1].spines['top'].set_visible(False)
ax[0].xaxis.tick_top()
ax[0].tick_params(labeltop=False)
ax[1].xaxis.tick_bottom()
# プロット切断部に点線表示を行う。
d = 0.01
kwargs = dict(transform=ax[0].transAxes, color='k',linestyle=':', lw=1, clip_on=False)
ax[0].plot((-d, 1+d), (0, 0), **kwargs)
kwargs.update(transform=ax[1].transAxes)
ax[1].plot((-d, 1+d), (1, 1), **kwargs)
# 上のaxesだけにlegendを表示するため、下のaxesではlegendを除去する。
ax[1].legend().remove()
plt.tight_layout()
plt.xticks(rotation=0)
plt.show()出力結果は以下の通りです。`keywords` は、名詞の割合が高いことや、`headline` には助詞と同じ割合で記号が含まれていることがわかります。
5.7.3. wordcloudによる可視化
単一テキスト、もしくはコーパス全体を可視化する主な手法として、そのコーパスに含まれる単語や形態素の頻度を可視化する方法があります。 ここではその代表的な手法であるwordcloudを用いたコーパス全体における単語の頻度情報の可視化を実施します。
単語の可視化を行う前に、分析のノイズとなる*stopwords*(どのテキストにおいても多く登場し、特に重要な意味を持たないもの)を取得し、それらを排除します。本解析では、名詞、動詞、形容詞、副詞以外をstopwordsとしています。なお、名詞でも数値の情報を含む場合はstopwordsとしています。
前節で記号情報を取得するため用いた、build_punctuations関数を少し変更し、stopwordsを取得するコードを作成します。おおよそのコードは同様ですが、大きな違いは、skip_flagsで取得する品詞型を定義するだけでなく、non_skip_flagsにより取得しない品詞型(数値)を定義する処理を追加しています。これは、名詞の品詞型を持つものの中で、数値の品詞型を持つものを取り除くために追加しています。なお、こちらのコードに関しても、実行時間短縮のためにすでにochasenよりparseされた情報を用いています。
def build_stopwords(parsed_by_ochasen, non_skip_flags=["数"], skip_flags = ["名詞", "動詞", "形容詞", "副詞"]):
gc.collect()
stopwords = set()
for parsed in tqdm(parsed_by_ochasen):
# non_skip_flagsが入っているものは全てstopwordsとして扱う
# それ以外において、skip_flagsをひとつでも含んでいないものをstopwordsとして扱う
mask_include_non_skip_flags = parsed['形態素の品詞型'].apply(lambda x: any([non_skip_flag in x.split('-') for non_skip_flag in non_skip_flags]))
mask_exclude_skip_flags = parsed['形態素の品詞型'].apply(lambda x: not any([skip_flag in x.split('-') for skip_flag in skip_flags]))
#日、月、年度のようなユニット情報を含むものは全てstopwordsとして扱う
mask_include_unit_info = parsed['表層形'].apply(lambda x: False if re.fullmatch(r'\d+(秒|分|時|日|月|カ月|年|人|ドル|円)', x) is None else True)
stopword_candidate = parsed['表層形'][mask_include_non_skip_flags | mask_exclude_skip_flags | mask_include_unit_info]
# stopwordsセットにアップデートする。
stopwords = stopwords | set(stopword_candidate.tolist())
# 追加的に単一アルファベットをstopwordsとして追加する
stopwords = stopwords | set(string.ascii_lowercase) | set(string.ascii_uppercase)
# 追加的に単一数字をstopwordsとして追加する
stopwords = stopwords | set([str(idx) for idx in range(10)])
return stopwords
# headline, keywords各々のコーパスからsubwordsを取得する。
headline_stopwords = build_stopwords(parsed_by_ochasen=parsed_headline_by_ochasen)
keywords_stopwords = build_stopwords(parsed_by_ochasen=parsed_keywords_by_ochasen) headline , keywords の各々から取得したstopwordsの集合を組み合わせています。
stopwords = headline_stopwords | keywords_stopwords
# 表示するためにリストに変換する。
stopwords_list = sorted(stopwords)
# 異なる特性を持つ色んなstopwordsを表示するためランダムにシャッフルする。
random.Random(0).shuffle(stopwords_list)
print(stopwords_list[:50])出力結果は以下の通りです。
['9302', '243', '456ドル', 'あれ', '2678', '259人', '182ドル', '3395円', '554', '9985', '1775', '100200', '510円', '2430円', '4918', '1114', '-', '1日', '7038', '向', '963', '9771円', '450ドル', '39日', '7068', '5カ月', '5168', '1001', '11分', '18年', '1931', '123', '1834', '4925円', '8分', '454ドル', '4788', '181人', '3097', '280', '3580円', '259円', '6156', '138ドル', '4347', 'm', '402', '8240', '417', '6600']単語の頻度可視化方法の1つとしてwordcloudというものがあります。この方法は、頻度順に字の大きさが異なる等、全体の傾向を直感的に把握しやすい長所がありますが、逆にそれ以上の知見をなかなか得られないという短所もあります。
wordcouldへの入力は、単語がスペースで区切られているテキストデータです。テキストデータ全体を入力とするには、テキストデータ全体が各々単語にスペースで区切られている必要があります。そのため文と文を区切る改行等を削除しスペースで区切るようにしています。具体的には、owakatiを用いてテキストデータをparseし、単語をスペースで区切り、その後テキスト毎にスペースで繋げています。
tagger = owakati
words_with_space = articles['headline'].apply(lambda x: tagger.parse(x).strip("\n").rstrip())
words_with_space = ' '.join(words_with_space)
# 確認する
print(words_with_space[:200])出力結果は以下の通りです。期待通りの結果になっていることがわかります。
日 米 貿易協定 が 発効 TPP 土台 に 自由貿易 圏 拡大 日本 、 RCEP に 波及 期待 人事 、 衆院 人事 、 外務省 人事 、 厚生労働省 「 雇用 制度 全般 の 見直し を 」 中西 経団連会長 経済3団体 トップ の 年頭 所感 首相 「 全世代 安心 の 社会保障 へ 改革 」 年頭 所感 天皇陛下 の 年頭 所感 全文 「 災害 が ない 1年 に 」 陛下 、 新年上記のコードをまとめ、wordcloudを可視化するための関数を定義しています。stopwordsに含まれる単語は表示対象から除外されています。
def display_wordcloud(tagger, texts, stopwords, collocations):
# textsがpd.Seriesでない時に、pd.Seriesに変換
if isinstance(texts, pd.Series) is False:
texts = pd.Series(texts)
# テキストは単語別にスペースで区切りされ、テキストごとはスペースでつながっていることが期待値
words_with_space = texts.apply(lambda x: tagger.parse(x).strip("\n").rstrip())
words_with_space = ' '.join(words_with_space)
# wordcloudを表示するため、パラメータを渡しインスタンス化する。
# collocations=Falseの場合、連語による重複単語が表示されない。
wordcloud = WordCloud(
background_color="white",
font_path=CONFIG['font_path'],
stopwords=stopwords,
width=2000,
height=1000,
collocations=collocations,
random_state=0,
).generate(words_with_space)
# 表示サイズを設定し、表示する。
fig, ax = plt.subplots(1, 1, figsize=(16, 8))
ax.imshow(wordcloud, interpolation="bilinear")
plt.axis("off")
plt.show()上記関数を用いて headline 及び keywords の各々のコーパスの頻度を可視化します。
# headlineのwordcloud表示
display_wordcloud(tagger=owakati, texts=articles['headline'], stopwords=stopwords, collocations=False)headlineのwordcloudは以下の通りです。

# keywordsのwordcloud表示
display_wordcloud(tagger=owakati, texts=articles['keywords'], stopwords=stopwords, collocations=False)keywordsのwordcloudは以下の通りです。

以上の結果から、以下のことが観察されます。
-
headlineに「人事」や「発売」、「コロナ」、「米」という単語が多く含まれていることがわかります。
-
keywordsには「新型」や「日」、「発表」という単語が多く含まれていることがわかります。
-
「東証」や「株式市場」などマーケット関連の単語が双方に多く含まれています。
-
「コロナ」や「コロナウィルス」などの新型コロナウィルスに関連する単語が双方に多く含まれています。
これらの観察結果に注意して、次のscatter textの解析を実施します。
5.7.4. scatter textによる可視化
頻度の可視化方法の一つに、頻度の情報だけでなく、その単語の一般性を表す使用分布も共に可視化できるscatter textというものがあります。
scatter textをプロットするにあたり、wordcloudと同様に各々の単語がスペースで区切られている必要があります。しかし、こちらはwordcloudとは違い、コーパス全体を一つとして繋げる必要はありません。まず、wordcloudの時と同様にowakatiより、テキストをparseし、単語をスペースより区切ります。
tokenized = articles['headline'].apply(lambda x: tagger.parse(x).strip("\n").rstrip())
# 確認する
tokenized.head(3)続き、whitespace_nlp_with_sentences関数をテキスト毎に適用します。
parsed = tokenized.apply(st.whitespace_nlp_with_sentences)
# 確認する
parsed.head(3)可視化のため、corpusインスタンスを作る必要があります。get_unigram_corpus関数を用いてbigramsをcorpusから取り除き、remove_terms関数よりstopwordsを取り除いています。また、remove_infrequent_words関数を用いて、出現頻度が100回以下の単語は除去しています。
corpus = st.CorpusWithoutCategoriesFromParsedDocuments(
parsed.rename('parse').to_frame(), parsed_col='parse'
).build().get_unigram_corpus().remove_terms(stopwords, ignore_absences=True).remove_infrequent_words(minimum_term_count=100)Dispersion関数を用いて、単語ごとの頻度情報及び使用分布情報を取得します。
dispersion = st.Dispersion(corpus)
dispersion_df = dispersion.get_df()
# ビルドされた頻度情報及び使用分布情報から、どの基準を用いてプロットするかをX, Xpos, Y, Yposのcolumnsにセットする。
dispersion_df = dispersion_df.assign(
X=lambda df: df.Frequency,
Xpos=lambda df: st.Scalers.log_scale(df.X),
Y=lambda df: df["Rosengren's S"],
Ypos=lambda df: st.Scalers.scale(df.Y),
)
# 確認する
dispersion_df.head(5)出力結果は以下の通りです。

これまでと同様に上記で作成したコードをまとめて、scatter text可視化を行う関数を作成しています。
def display_scatter_text(tagger, texts, stopwords, filename='out'):
gc.collect()
# textsがpd.Seriesでない時に、pd.Seriesに変換。
if isinstance(texts, pd.Series) is False:
texts = pd.Series(texts)
# owakatiより、テキストをparseし、単語をスペースで区切り、whitespace_nlp_with_sentencesを適用。
tokenized = texts.apply(lambda x: tagger.parse(x).strip("\n").rstrip())
parsed = tokenized.apply(st.whitespace_nlp_with_sentences)
# bigrams及びstopwordsをcorpusから取り除き、出現頻度が100回以下の単語を除去する。
corpus = st.CorpusWithoutCategoriesFromParsedDocuments(
parsed.rename('parse').to_frame(), parsed_col='parse'
).build().get_unigram_corpus().remove_terms(stopwords, ignore_absences=True).remove_infrequent_words(minimum_term_count=100)
# Dispersion関数をより、単語ごとの頻度情報及び使用分布情報を取得。
dispersion = st.Dispersion(corpus)
dispersion_df = dispersion.get_df()
dispersion_df = dispersion_df.assign(
X=lambda df: df.Frequency,
Xpos=lambda df: st.Scalers.log_scale(df.X),
Y=lambda df: df["Rosengren's S"],
Ypos=lambda df: st.Scalers.scale(df.Y),
)
# dataframe_scattertext関数より、可視化したhtmlをビルドできる。
html = st.dataframe_scattertext(
corpus,
plot_df=dispersion_df,
ignore_categories=True,
x_label='Log Frequency',
y_label="Rosengren's S",
y_axis_labels=['More Dispersion', 'Medium', 'Less Dispersion'],
)
# htmlを書き出します。Google Driveの該当箇所に出力されるため、出力されたhtmlファイルをダウンロードし、ブラウザで開いて御覧ください。
open(f'{CONFIG["base_path"]}/visualizations/vis_{filename}_scatter.html', 'w').write(html) ここまで準備ができたら、まずは headline のテキストデータを用いてscatter text可視化を行います。
# 以下のコードを実行するとvisualizations配下にhtmlファイルが作成されます。作成されたファイルをブラウザで開いて確認ください。
display_scatter_text(tagger=owakati, texts=articles['headline'], stopwords=stopwords, filename='headline')出力結果は以下の通りです。
縦軸(y軸)は使用分布(Dispersion)を表します。y軸のDispersionは特定の単語がコーパス内でどれだけ均等に分布しているかを表す数値で、1 (Less Dispersion)に近いほどどのコーパスにも均等に現れる単語であり、0 (More Dispersion) に近いほど特定の分野でのみ現れていることを示しています。横軸(x軸)はコーパス全体における単語の使用頻度の対数スケールで表示しています。カーソルを単語に重ねると各単語の数値が表示されます。
この図からも「米」、「コロナ」、「株式市場」、「人事」などの単語が多く使用されていることが分かります。これはwordcloudで観察した結果と似ています。さらに注目すべき点は、「人事」は使用頻度が高いにもかかわらず、使用分布が狭く、特定の分野でのみ使用されていることが分かります。この結果から、この単語を含むテキストはコーパス全体と性質が異なると想定できます。この単語が有意味な情報を含むかを判断し、追加的な前処理を実施する必要があるかを後ほど検討します。
引き続き、 keywords のコーパスを用いてscatter text可視化を行います。
display_scatter_text(tagger=owakati, texts=articles['keywords'], stopwords=stopwords, filename='keywords')出力結果は以下の通りです。
keywords に関しても、「コロナウイルス」や、「株式市場」などが高頻度単語として観察されています。headlineにおける「人事」のような使用頻度と使用分布に著しい違いがある単語は観測できません。さらに追加的に解析を行いたい場合、品詞ごとにこれらの頻度や使用分布を可視化して解析することができます。品詞毎に、どのような単語が多く使われ、どのように分布しているかを観察し、コーパスの特性をさらに深く理解してみましょう。
5.7.5. トピック解析
コーパス全体の特性を理解するために、そのコーパス全体がどのようなトピックで構成されているかを解析するトピックモデリングの手法があります。潜在ディリクレ配分法(Latent Dirichlet Allocation, LDA)は、その中でもトピックモデリングの代表的アルゴリズムです。
LDAはコーパスがトピックの混合で成り立っていて、そのトピックが確率分布に従って単語を生成していると仮定し、その生成過程を逆に辿ることより、コーパス全体を構成するトピック情報を推定しています。LDAの学習時には、単語の頻度情報を持つメトリクスが用いられます。単語数が多くなり、メトリクスが大きくなるほど計算リソースが要求されます。ここでは現実的な処理時間で完了させるため、名詞以外の単語は全て取り除き解析しています。
build_stopwords関数を用いて、品詞情報が名詞以外のものを全てinvalid_tokensとして扱っています。また、名詞の中でも数を品詞型として含む場合も同様にinvalid_tokensとして扱っています。
def build_invalid_tokens(parsed_by_ochasen, non_skip_flags=['数'], skip_flags = ["名詞"]):
return build_stopwords(parsed_by_ochasen=parsed_by_ochasen, non_skip_flags=non_skip_flags, skip_flags=skip_flags)LDAの学習のために、owakatiを用いてトークナイズし、上記で定義したinvalid_tokensに含まれない名詞のみの単語にしています。
def tokenize_for_lda(tagger, texts, invalid_tokens):
# textsがpd.Seriesでない時に、pd.Seriesに変換
if isinstance(texts, pd.Series) is False:
texts = pd.Series(texts)
# owakatiを用いてトークナイズする
tokenized = texts.apply(lambda x: tagger.parse(x).split())
# 上記で定義したinvalid_tokensに含まれないトークンに精製する。
tokenized = tokenized.apply(lambda x: [token for token in x if token not in invalid_tokens])
return tokenized上記のtokenize_for_lda関数を用いてトークナイズし、その後単語のid、頻度をもつdictionaryを作り、gensim.models.ldamodel.LdaModelを用いてLDAを学習します。
def build_ldamodel(tagger, texts, invalid_tokens, num_topics=10):
tokenized = tokenize_for_lda(tagger=tagger, texts=texts, invalid_tokens=invalid_tokens)
# 頻度情報をもつ単語辞書を作る
dictionary = gensim.corpora.Dictionary(tokenized)
# 生成されたcorpusは(word_id, word_frequency)の情報を持つ
corpus = [dictionary.doc2bow(text) for text in tokenized]
ldamodel = gensim.models.ldamodel.LdaModel(corpus, num_topics=num_topics, id2word=dictionary, chunksize=5000, passes=10, random_state=0)
return ldamodel, corpus上記で作成したコードを用いて可視化を行います。以下のトピック解析コードは高い計算リソースが要求され、長い実行時間が必要ですので、そのことに留意し実行しましょう。
ここでは二つの可視化を行います。まず、LDAモデルより推定されたトピックがどのような単語と関連が深いかを表示します。これにより、コーパス全体をクラスター化でき、それぞれのクラスターがどのような特性や性質を持つか理解することができます。その後、トピック(クラスター)ごとの分布を可視化します。これにより、トピックのコーパスに対する寄与度(周辺確率分布)やトピック間の距離などを確認できます。
# headline, keywords両方において可視化を行う。
for column in ['headline', 'keywords']:
parsed_by_ochasen = {
'headline': parsed_headline_by_ochasen,
'keywords': parsed_keywords_by_ochasen,
}[column]
invalid_tokens = build_invalid_tokens(parsed_by_ochasen=parsed_by_ochasen)
ldamodel, corpus = build_ldamodel(tagger=owakati, texts=articles[column], invalid_tokens=invalid_tokens)
display_markdown(f'#### column: {column}', raw=True)
# 推定されたtopicと関連深い上位5つの単語をプリントする
for topic in ldamodel.print_topics(num_words=5):
print(topic)
# トピック可視化
# 可視化したトピックのidが0ではなく1から始まることに注意しましょう。
# 左方の円は、各々の10個のトピックを表す。
# 各円との距離は、それぞれトピックがどれだけ離れているかを表す。
vis = pyLDAvis.gensim.prepare(ldamodel, corpus, ldamodel.id2word, sort_topics=False)
# htmlを書き出します。出力されたhtmlファイルをダウンロードし、ブラウザで開いて御覧ください。
pyLDAvis.save_html(vis, f'{CONFIG["base_path"]}/visualizations/vis_{column}_lda.html') headline のトピックと関連する上位5つの単語の出力は以下の通りです。「米」と「中国」が同一のトピックに登場しやすいこと、「新型コロナ」、「感染」、「対策」が同一のトピックに登場しやすいことなど、直感に反しない結果が取得できていることがわかります。
column: headline
(0, '0.035*"減" + 0.030*"月" + 0.025*"期" + 0.024*"増" + 0.018*"東証"')
(1, '0.022*"新型コロナ" + 0.019*"感染" + 0.009*"対策" + 0.009*"発行" + 0.008*"知事"')
(2, '0.014*"政府" + 0.013*"バイデン" + 0.013*"オンライン" + 0.012*"欧州" + 0.011*"米"')
(3, '0.048*"発売" + 0.011*"用" + 0.011*"型" + 0.007*"発表" + 0.006*"シリーズ"')
(4, '0.056*"コロナ" + 0.030*"株" + 0.026*"米" + 0.021*"ぶり" + 0.017*"上昇"')
(5, '0.014*"支援" + 0.013*"開始" + 0.012*"連携" + 0.010*"サービス" + 0.008*"活用"')
(6, '0.060*"氏" + 0.023*"社長" + 0.016*"中国" + 0.012*"生産" + 0.010*"米"')
(7, '0.015*"米国" + 0.012*"ロンドン" + 0.011*"発表" + 0.009*"市場" + 0.009*"年末年始"')
(8, '0.112*"人事" + 0.014*"AI" + 0.014*"開発" + 0.009*"DX" + 0.007*"技術"')
(9, '0.016*"発表" + 0.013*"調査" + 0.009*"機能" + 0.009*"県" + 0.009*"推進"') 各単語の前にある数値は、該当するトピックへの寄与度を表しています。コーパスを10個のトピックに分類した時に、それぞれのトピックの特性を寄与する単語から理解することができます。次に、pyLDAvisを用いて headline のトピックを可視化しています。
ここからさらに細かな分析を行うことができます。上の左図の円はそれぞれのトピックを表しています。可視化におけるトピックの番号は1から始まることにご注意ください。各円間の距離は、トピックがそれぞれどれほど異なるかを表し、近いほど似ているトピックであることを表します。
keywords のトピックとそれに関連する上位5つの単語の出力は以下の通りです。こちらもコロナウィルス関連や株式市場関連など、直感に反しない結果となっています。
column: keywords
(0, '0.019*"大学" + 0.014*"教授" + 0.010*"検査" + 0.009*"医療" + 0.008*"ポイント"')
(1, '0.050*"コロナ" + 0.019*"社長" + 0.011*"生産" + 0.011*"工場" + 0.010*"中国"')
(2, '0.059*"日" + 0.057*"発表" + 0.032*"新製品" + 0.020*"株式会社" + 0.011*"販売"')
(3, '0.029*"連結決算" + 0.028*"売上高" + 0.025*"純利益" + 0.024*"減益" + 0.024*"決算"')
(4, '0.025*"政府" + 0.019*"首相" + 0.019*"米国政府" + 0.016*"大統領" + 0.013*"米国"')
(5, '0.014*"コロナ禍" + 0.011*"オンライン" + 0.008*"イベント" + 0.007*"時代" + 0.006*"サッカー"')
(6, '0.019*"動向" + 0.017*"民間" + 0.015*"市場" + 0.015*"統計" + 0.013*"政府統計"')
(7, '0.046*"新型" + 0.042*"ウイルス" + 0.039*"コロナウイルス" + 0.026*"感染" + 0.024*"株式市場"')
(8, '0.018*"株" + 0.017*"ロンドン" + 0.013*"投資" + 0.013*"外為市場" + 0.012*"ドル"')
(9, '0.009*"事業" + 0.009*"連携" + 0.008*"AI" + 0.007*"業務提携" + 0.007*"GoTo"')次に、pyLDAvisを用いた keywords のトピックを可視化しています。
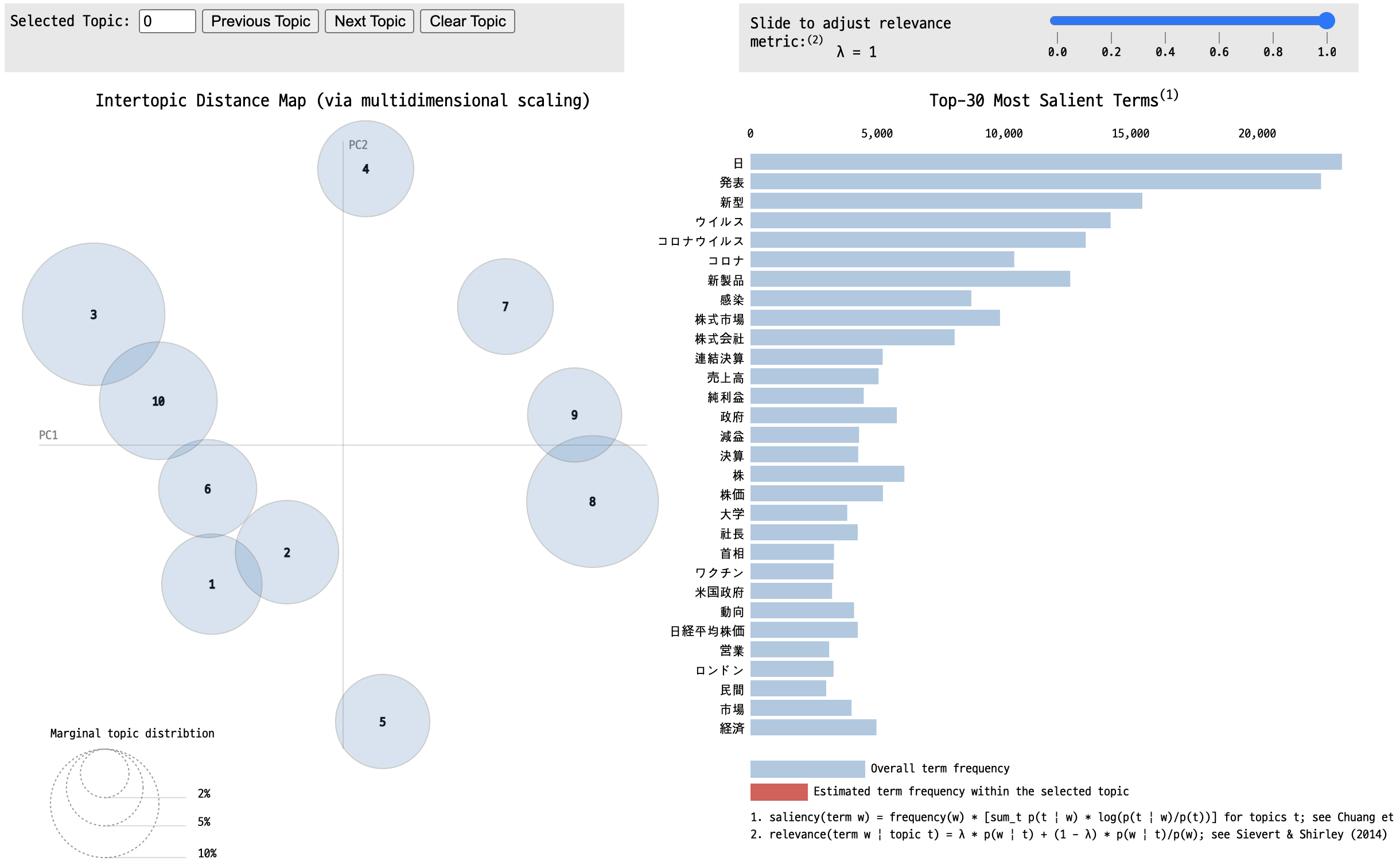
5.7.6. 解析結果を活用した追加的なデータの前処理
ここまでの解析によって得られた知見から、追加的なデータの前処理を検討します。テキスト内にノイズとなり得る単語の規則性が確認できた場合や、テキスト自体が無意味であるかノイズとなり得る場合がないかを考察しましょう。
前章での可視化及び解析を通じて、コーパス全体において、「人事」という単語が非常に高い頻度で観測されていました。しかし、CEO等の交代がプラスの効果を持つか、マイナスの効果を持つかはケースバイケースと思われるため、各社の人事情報をマーケットの予測に役立てる難易度は非常に高いと想定されます。このような仮説を基に、本チュートリアルでは人事の内容を含むニュースを除去しています。
# owakatiを用いて、'人事'の単語を含む記事を除去する方法もあるが、本番環境でのリソースを軽減させるため、単純に文字列から人事を含む全てのニュースの除去を行う。
# headlineもしくは、keywordsどちらかで人事を含むニュース記事のindexマスクを作成。
drop_mask = articles['headline'].str.contains('人事') | articles['keywords'].str.contains('人事')
# '人事'を含む例を表示する
articles[drop_mask].head()出力結果は以下の通りです。

'人事'という単語を含むニュースを取り除きます。
articles = articles[~drop_mask]
# '人事'を含むニュースが存在するか確認する。
(articles['headline'].str.contains('人事') | articles['keywords'].str.contains('人事')).any()出力結果は以下の通りです。人事を含むニュースが存在しないことが分かり、正しく取り除くことができています。
False5.7.7. 本番提出用のクラスへ組み込み
ここまでの処理をdrop_remove_list_words関数として SentimentGenerator クラスに追加します。
#上記のコードを用いて、本番提出用のクラスにclassmethodを追加
@classmethod
def drop_remove_list_words(cls, articles, remove_list_words=["人事"]):
articles = articles.copy()
for remove_list_word in remove_list_words:
# headlineもしくは、keywordsどちらかでremove_list_wordを含むニュース記事のindexマスクを作成
drop_mask = articles["headline"].str.contains(remove_list_word) | articles[
"keywords"
].str.contains(remove_list_word)
# remove_list_wordを含まないニュースだけに精製する。
articles = articles[~drop_mask]
return articles
# SentimentGeneratorに定義したclassmethodを追加する
SentimentGenerator.drop_remove_list_words = drop_remove_list_words
# SentimentGeneratorに使用する全体の流れを記述
articles = SentimentGenerator.load_articles(path=CONFIG["article_path"])
articles = SentimentGenerator.normalize_articles(articles)
articles = SentimentGenerator.handle_punctuations_in_articles(articles)
articles = SentimentGenerator.drop_remove_list_words(articles)5.8. 特徴量抽出機、前処理機の定義
ここまでの前処理等を踏まえ、BERTへテキストデータを投入する準備が整いました。ここからはBERTモデルを扱う上で必要な特徴量抽出時に使うデバイス(GPU)の定義、特徴量抽出のためのBERTモデルの定義、BERTモデルに係る前処理の定義等を行っていきます。
5.8.1. 本番提出用のクラスへ組み込み
SentimentGenerator クラスに複数の関数を追加していきます。
@classmethod
def _set_device(cls):
# 使用可能なgpuがある場合、そちらを利用し特徴量抽出を行う
if torch.cuda.device_count() >= 1:
cls.device = 'cuda'
print("[+] Set Device: GPU")
else:
cls.device = 'cpu'
print("[+] Set Device: CPU")
@classmethod
def _build_feature_extractor(cls):
# 特徴量抽出のため事前学習済みBERTモデルを用いる。
# ここでは、"cl-tohoku/bert-base-japanese-whole-word-masking"モデルを使用しているが、異なる日本語BERTモデルを用いても良い。
cls.feature_extractor = (
transformers.BertModel.from_pretrained(
"cl-tohoku/bert-base-japanese-whole-word-masking",
return_dict=True,
output_hidden_states=True,
)
)
# 使用するdeviceを指定
cls.feature_extractor = cls.feature_extractor.to(cls.device)
# 今回は特徴量抽出を行うのみであり、この事前モデル学習は行わないため、評価モードにセットする。
cls.feature_extractor.eval()
print("[+] Built feature extractor")
@classmethod
def _build_tokenizer(cls):
# BERTモデルの入力とするコーパスはそのBERTモデルが学習された時と同様の前処理を行う必要がある。
# 今回使用する"cl-tohoku/bert-base-japanese-whole-word-masking"モデルは、mecab-ipadic-NEologdによりトークナイズされ、その後Wordpiece subword encoderよりsubword化している。
# Subwordとは形態素に類似な概念として、単語をより小さい意味のある単位に変換したものである。
# transformersのBertJapaneseTokenizerを用いることで、その事前学習モデルの学習時と同様の前処理を簡単に使用することができる。
# そのため、ここではBertJapaneseTokenizerを利用し、トークナイズ及びsubword化を行う。
cls.bert_tokenizer = BertJapaneseTokenizer.from_pretrained("cl-tohoku/bert-base-japanese-whole-word-masking")
print("[+] Built bert tokenizer")
# SentimentGeneratorに定義したclassmethodを追加する
SentimentGenerator._set_device = _set_device
SentimentGenerator._build_feature_extractor = _build_feature_extractor
SentimentGenerator._build_tokenizer = _build_tokenizer
# SentimentGenerator使用する全体流れを記述
articles = SentimentGenerator.load_articles(path=CONFIG["article_path"])
articles = SentimentGenerator.normalize_articles(articles)
articles = SentimentGenerator.handle_punctuations_in_articles(articles)
articles = SentimentGenerator.drop_remove_list_words(articles)
SentimentGenerator._set_device()
SentimentGenerator._build_feature_extractor()
SentimentGenerator._build_tokenizer()5.8.2. BERTモデルを使用するための前処理
本節では以下の2つの異なるトークナイザを用いてトークナイズした結果を比較し、それぞれの前処理の違いを確認してみます。
-
SentimentGenerator.bert_tokenizer: mecab-ipadic-NEologd + Wordpiece
-
owakati: mecab-ipadic-NEologd
text = '我らは走り出す。'
display(SentimentGenerator.bert_tokenizer.tokenize(text))
display(owakati.parse(text).split())出力結果は以下の通りです。Subword化を行うbert_tokenizerの方がより小さい単位でトークン化されていることがわかります。このようなsubwordを用いると、学習時に出現していない単語(Out-of-Vocabulary)に関する問題を緩和させることができます。
['我', '##ら', 'は', '走り', '##出す', '。']
['我ら', 'は', '走り出す', '。']基本的にどのような言語モデルもトークナイズ後のトークンをそのまま受け取ることはできません。トークンを数字に対応させるためのid化が必要となります。事前学習モデルを用いる場合、各々のトークンはすでにidが付与されているため、モデルに入力するトークンデータをそのidに変換した上で、モデルの入力とする必要があります。BertJapaneseTokenizerのencodeメソッドはこのようなid化を行ってくれます。
display(SentimentGenerator.bert_tokenizer.encode(text))出力結果は以下の通りです。
[2, 3706, 28469, 9, 7498, 2813, 8, 3]以下のコードよりid化したトークンを、再びトークンに変換してみましょう。
for id in SentimentGenerator.bert_tokenizer.encode(text):
print(f'{id}: {SentimentGenerator.bert_tokenizer.decode(id)}')出力結果は以下の通りです。
2: [ C L S ]
3706: 我
28469: # # ら
9: は
7498: 走 り
2813: # # 出 す
8: 。
3: [ S E P ]idをトークンに再び戻した時、元のデータには存在していなかった[CLS]と[SEP]が現れていることがわかります。この二つは `special tokens `と呼ばれ、[CLS]は全ての文章の先頭に位置し、文章の分類タスクを行う際に用いられるものです。また、[SEP]は複数の文章を区切るために用いられます。BERTへの入力は、必ずこのフォーマットに従う必要があります。
BERTの入力値は上記で生成したtokenのids以外に, token_type_ids , attention_mask のベクトルを入力として受け取ります。 token_type_ids は複数の文章を区切るため用いられ、 attention mask は実際にトークンが存在する部分とzero paddingされた部分を区切るため用いられます。SentimentGenerator.bert_tokenizer.encode_plusメソッドによりこれらのベクトルを作ることができます。
encoded = SentimentGenerator.bert_tokenizer.encode_plus(
text,
None,
add_special_tokens=True,
return_token_type_ids=True,
truncation=True,
)
# 確認する
encoded出力結果は以下の通りです。
{'input_ids': [2, 3706, 28469, 9, 7498, 2813, 8, 3], 'token_type_ids': [0, 0, 0, 0, 0, 0, 0, 0], 'attention_mask': [1, 1, 1, 1, 1, 1, 1, 1]}これらはtorchモデルに入力するためにtensor形式に変換し、deviceを指定する必要があります。
input_ids = torch.tensor([encoded['input_ids']], dtype=torch.long).to(SentimentGenerator.device)
token_type_ids = torch.tensor([encoded['token_type_ids']], dtype=torch.long).to(SentimentGenerator.device)
attention_mask = torch.tensor([encoded['attention_mask']], dtype=torch.long).to(SentimentGenerator.device)
# 確認する
display(input_ids)
display(token_type_ids)
display(attention_mask)出力結果は以下の通りです。
tensor([[ 2, 3706, 28469, 9, 7498, 2813, 8, 3]])
tensor([[0, 0, 0, 0, 0, 0, 0, 0]])
tensor([[1, 1, 1, 1, 1, 1, 1, 1]])5.8.3. 特徴量抽出
前処理の最後で取得した三つのベクトル[input_ids, token_type_ids, attention_mask]をBERTモデルへ入力し、そのoutputを取得します。
output = SentimentGenerator.feature_extractor(input_ids=input_ids, token_type_ids=token_type_ids, attention_mask=attention_mask)
# outputをdictionary形式に変換し、その中からどのようなkeyが存在するかをみてみる。
output.__dict__.keys()存在しているkeyは以下の通りです。
dict_keys(['last_hidden_state', 'pooler_output', 'hidden_states', 'past_key_values', 'attentions', 'cross_attentions'])各keyから取得できる情報は以下の通りです。
-
last_hidden_stateにはモデルの最終層のhidden stateが格納されています。 -
pooler_outputにはモデル最終層出力の最初のトークンのhidden stateが格納されています。 -
hidden_statesにはモデル各層の出力全てのhidden stateが格納されています。 -
attentionsはattention softmax以降のattentions weightsが格納されています。 -
cross_attentionsはdecoderのcross-attention層における、attention softmax以降のattentions weightsが格納されています。
一般的にBERTの特徴量とは、最終層の一つ前のhidden stateを指します。本チュートリアルでも、最終層の一つ前のhidden stateを抽出し、特徴量として用いています。
hidden stateについて、最終層ではなく最終層の手前の情報を利用する理由は、最終層は個々の学習タスクに強く関連情報を持つことから、特徴量抽出には一般的により豊富な情報を持つ最終層の手前を使用します。この内容に関してより詳しく知りたい場合はこちらをご参照下さい。
以下のコードより特徴量を取得します。
features = output['hidden_states'][-2]
# 確認する。
display(features)
display(features.size())出力結果は以下の通りです。
tensor([[[-0.4128, -0.1108, -0.6859, ..., 0.5316, 0.3867, 0.4347],
[ 0.7700, 0.0892, 0.7817, ..., -1.0288, 0.4230, -0.8906],
[ 1.2572, 0.3211, -0.6861, ..., 0.0815, 0.7084, -1.0055],
...,
[ 1.0648, -1.3369, -0.2810, ..., 0.5657, 0.7713, -0.6337],
[-0.3294, -0.3912, 0.2754, ..., -0.0620, 1.1760, -0.9139],
[ 0.0639, 0.2225, 0.0474, ..., 0.1486, 0.0587, 0.0557]]],
grad_fn=<NativeLayerNormBackward>)
torch.Size([1, 8, 768]) features の次元を見ると、[1, 8, 768]の次元を持つことがわかります。これらは各々順番に[データ数、シーケンスサイズ、hidden stateのサイズ]を表しています。一つ注意すべきところは、長さの異なるsequenceを入力すると、以下のようにベクトルのサイズが変わってくることです。
text = 'こちらでは、より長い文章を用いて特徴量を抽出してみましょう。'
encoded = SentimentGenerator.bert_tokenizer.encode_plus(
text,
None,
add_special_tokens=True,
return_token_type_ids=True,
truncation=True,
)
input_ids = torch.tensor([encoded['input_ids']], dtype=torch.long).to(SentimentGenerator.device)
token_type_ids = torch.tensor([encoded['token_type_ids']], dtype=torch.long).to(SentimentGenerator.device)
attention_mask = torch.tensor([encoded['attention_mask']], dtype=torch.long).to(SentimentGenerator.device)
output = SentimentGenerator.feature_extractor(input_ids=input_ids, token_type_ids=token_type_ids, attention_mask=attention_mask)
features = output['hidden_states'][-2]
# 確認する
features.size()出力結果は以下の通りです。dimension1のシーケンスサイズの箇所の次元が変わっていることがわかります。
torch.Size([1, 22, 768])本チュートリアルではdimension1の次元を平均化し特徴量として扱うため、シークエンスの違いはそれほど問題とはなりませんが、並列化する上では問題となります。シーケンスの異なるベクトルを重ねることができないからです。このような問題を扱うため、subwordsのシーケンスのmax_lengthを決め、それより短い場合はmax_lengthの長さとなるように、ベクトルの末端を0で埋めるzero paddingがよく使われます。前処理を行う際にmax_lengthのパラメータを渡し、padding='max_legnth'を指定すると、max_lengthの長さがなるようにzero paddingすることができます。
text = 'こちらでは、より長い文章を用いて特徴量を抽出してみましょう。'
encoded = SentimentGenerator.bert_tokenizer.encode_plus(
text,
None,
max_length=512,
padding='max_length',
add_special_tokens=True,
return_token_type_ids=True,
truncation=True,
)
# 確認する
encoded出力結果は以下の通りです。zero paddingされていることがわかります。
{'input_ids': [2, 4871, 12, 9, 6, 221, 2894, 7204, 11, 585, 16, 1427, 1073, 11, 11674, 15, 16, 546, 17015, 205, 8, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], 'token_type_ids': [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], 'attention_mask': [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]}それでは、異なる長さを持つ複数の文章を用いて、paddingされたinputをモデルに同時に入力し並列に処理されるか確認してみましょう。
texts = ['短いテキスト', '少し長いテキストです', '長い長い長い長いテキストです']
input_ids = []
token_type_ids = []
attention_mask = []
for text in texts:
encoded = SentimentGenerator.bert_tokenizer.encode_plus(
text,
None,
add_special_tokens=True,
max_length=512,
padding="max_length",
return_token_type_ids=True,
truncation=True,
)
input_ids.append(encoded['input_ids'])
token_type_ids.append(encoded['token_type_ids'])
attention_mask.append(encoded['attention_mask'])
input_ids = torch.tensor(input_ids, dtype=torch.long).to(SentimentGenerator.device)
token_type_ids = torch.tensor(token_type_ids, dtype=torch.long).to(SentimentGenerator.device)
attention_mask = torch.tensor(attention_mask, dtype=torch.long).to(SentimentGenerator.device)
output = SentimentGenerator.feature_extractor(input_ids=input_ids, token_type_ids=token_type_ids, attention_mask=attention_mask)
features = output['hidden_states'][-2]
# 確認する
features.size()出力結果は以下の通りです。[3つの文章、シーケンスの長さ、hidden state]の次元の特徴量を取得でき、dimention1は指定したmax_lengthである512に一致していることがわかリます。
torch.Size([3, 512, 768])本チュートリアルでは最終的に、dimension1を平均化して、各テキストごとに768次元のベクトルを特徴量として抽出します。
features = features.mean(dim=1)
# 確認する
features.size()出力結果は以下の通りです。
torch.Size([3, 768])5.8.4. 本番提出用のクラスへ組み込み
上記のコードを纏め、テキストから前処理を行い、モデル入力に必要な各々のベクトルを返す関数を SentimentGenerator クラスに追加します。
@classmethod
def build_inputs(cls, texts, max_length=512):
input_ids = []
token_type_ids = []
attention_mask = []
for text in texts:
encoded = cls.bert_tokenizer.encode_plus(
text,
None,
add_special_tokens=True,
max_length=max_length,
padding="max_length",
return_token_type_ids=True,
truncation=True,
)
input_ids.append(encoded['input_ids'])
token_type_ids.append(encoded['token_type_ids'])
attention_mask.append(encoded['attention_mask'])
# torchモデルに入力するためにはtensor形式に変え、deviceを指定する必要がある。
input_ids = torch.tensor(input_ids, dtype=torch.long).to(cls.device)
token_type_ids = torch.tensor(token_type_ids, dtype=torch.long).to(cls.device)
attention_mask = torch.tensor(attention_mask, dtype=torch.long).to(cls.device)
return input_ids, token_type_ids, attention_mask
# 上記のコードでビルドしたベクトルをモデルに入力し、特徴量を抽出するコードを作成
@classmethod
def generate_features(cls, input_ids, token_type_ids, attention_mask):
output = cls.feature_extractor(input_ids=input_ids, token_type_ids=token_type_ids, attention_mask=attention_mask)
features = output['hidden_states'][-2].mean(dim=1).cpu().detach().numpy()
return features
# コーパス全体から特徴量を抽出するため、コーパス全体を同時にモデルへ入力することはメモリーの上限を遥かに超えてしまうので不可能に近い。
# 入力するコーパスを数回に分割し、上記で作成したコードbuild_inputsとgenerate_featuresを用いて並列化処理を行うため、以下のコードを作成する。
@classmethod
def generate_features_by_texts(cls, texts, batch_size=2, max_length=512):
n_batch = math.ceil(len(texts) / batch_size)
features = []
for idx in tqdm(range(n_batch)):
input_ids, token_type_ids, attention_mask = cls.build_inputs(texts=texts[batch_size*idx:batch_size*(idx+1)], max_length=max_length)
features.append(cls.generate_features(input_ids=input_ids, token_type_ids=token_type_ids, attention_mask=attention_mask))
features = np.concatenate(features, axis=0)
# 抽出した特徴量はnp.ndarray形式となっており、これらは、日付の情報を失っているため、pd.DataFrame形式に変換する。
return pd.DataFrame(features, index=texts.index)
# SentimentGeneratorに定義したclassmethodを追加する
SentimentGenerator.build_inputs = build_inputs
SentimentGenerator.generate_features = generate_features
SentimentGenerator.generate_features_by_texts = generate_features_by_texts
# SentimentGenerator使用する全体流れを記述
articles = SentimentGenerator.load_articles(path=CONFIG["article_path"])
articles = SentimentGenerator.normalize_articles(articles)
articles = SentimentGenerator.handle_punctuations_in_articles(articles)
articles = SentimentGenerator.drop_remove_list_words(articles)
SentimentGenerator._set_device()
SentimentGenerator._build_feature_extractor()
SentimentGenerator._build_tokenizer()
# 以下のコードでコーパス全体の特徴量を抽出できる。しかし、抽出には長い時間が要求されるため、注意。
headline_features = SentimentGenerator.generate_features_by_texts(texts=articles['headline'])
keywords_features = SentimentGenerator.generate_features_by_texts(texts=articles['keywords'])それでは上記のコードを実行し特徴量を抽出してみましょう。この処理は非常に時間がかかる(GPUがある環境で数時間、GPUがないと数十時間必要)ため、実行結果はPKLファイルで別途提供致します。詳細は5.2. 実行環境をご参照ください。もし、ご自分の環境で特徴量抽出を実行した場合は、その結果を以下のようにPKLファイルで保存しておくことをおすすめします。
# pklファイルとして保存しておく。
headline_features.to_pickle(f'{CONFIG["base_path"]}/headline_features/headline_features.pkl')
keywords_features.to_pickle(f'{CONFIG["base_path"]}/keywords_features/keywords_features.pkl')5.8.5. PCAによるスコア化
BERTで作成した特徴量は高次元の特徴量であり、機械学習モデルで利用する場合には、なんらかの単一のスコアに変換する必要があります。
データの次元圧縮テクニックの一つとして主成分分析(PCA:principal component analysis)があります。主成分分析とは、多変量解析手法のうち次元削減手法としてよく用いられる手法の一種で、相関のある多変数から、相関のない少数で全体のばらつきを最もよく表す変数を合成するものです。(引用:Qiita:主成分分析を Python で理解する)。PCAには通常のPCAとカーネルPCAがあり、2つの挙動はそれぞれ異なるので、用途などを考慮して使うものを決めます。 ( 引用: カーネル主成分分析とは )。
例えば、以下のようなコードでPCAを用いて次元圧縮をすることで、BERTで作成した特徴量は単一のスコアになり、機械学習モデルの特徴量として扱いやすくなります。
# 次元圧縮関数(PCA/KPCA)の定義
def _build_compressor(compress_method):
assert compress_method in ('pca', 'kpca')
if compress_method == 'pca':
return PCA(n_components=1)
if compress_method == 'kpca':
return KernelPCA(kernel='rbf', n_components=1)
# 次元圧縮処理を実施する関数
def compress_feature_n_samples(features, compress_method, max_samples=500):
feature_compressor = _build_compressor(compress_method=compress_method)
compressed_features = pd.Series(feature_compressor.fit_transform(features).reshape(-1), index=features.index)
sample_compressor = _build_compressor(compress_method=compress_method)
weekly_group = pd.Series(zip(compressed_features.index.year, compressed_features.index.week), index=compressed_features.index)
grouped_compressed_features = compressed_features.groupby(weekly_group).apply(lambda x: x[-max_samples:].reset_index(drop=True)).unstack()
return pd.Series(sample_compressor.fit_transform(grouped_compressed_features).reshape(-1), index=grouped_compressed_features.index)
# 上記関数を用いてスコアを生成しPKLファイルに保存しています。モデルやバックテストに利用可能です。
for features, feature_type in [(headline_features, 'headline_features'), (keywords_features, 'keywords_features')]:
for compress_method in ['pca']:
compress_feature_n_samples(features=features, compress_method=compress_method).to_pickle(f'{feature_type}_{compress_method}.pkl')ここで取得したPCAのスコアは、何か目的をもって学習させたものではないため、単体でポートフォリオに利用するのは難しいと思われますが、機械学習モデルの特徴量として、例えばrandom forestのモデルなどにはそのままPCAスコアを投入することが可能です。よりシンプルな利用方法として、例えばPCAのスコアと連動しやすい銘柄について相関係数などを利用して解析し、PCAスコアに合わせて次週の取引対象銘柄を限定するようなアプローチも考えられます。
本章ではBERTを用いてニュースデータから特徴量抽出を行ってきました。本章の最後に紹介したPCAによる次元圧縮では、圧縮時に目的関数を設定することはできないために、特定の目的のためのスコアとは言えません。そこで次章では、リカレントニューラルネットワークであるLSTMを用いて、週毎の可変な特徴量を統合し単一のスコアにする手法を紹介し、このスコアを活用する方法を紹介していきます。
6. BERT特徴量を用いてポートフォリオを構築しよう
5章ではBERTを用いた特徴量抽出および簡単なPCAによるスコア化の手法を紹介しました。PCAは次元圧縮の代表的な手法ですが、次元圧縮時に目的関数を設定することができないために、特定の目的に合わせたスコアではありません。
そのため,本章ではLSTMを用いて、週毎の可変な特徴量を統合し単一のスコアにする手法を紹介します。この手法を紹介する理由は、LSTMは目的関数を設定することができ、BERT特徴量から特定の目的に合致したスコアを構築することが可能となるためです。実際に特徴量を活用する場合は、その特徴量を用いて何かを予測したいと考えることが多く、目的変数を設定できるレイヤーを構築して、用途に特化したスコアを活用することがを可能となり、応用可能性が広がります。
なお、本章はLSTMのようなディープニューラルネットワークを活用することに習熟している方を対象としており、アドバンスな知識を前提とした章となります。そのため、ディープニューラルネットワーク自体の説明はありません。5章で抽出した特徴量でも様々な活用が可能ですので、本章は発展的な内容としてご活用ください。
本章の最後では、5章および6章のコードを使用したポートフォリオ構築モデルの実装例と動作確認方法を記載しているため、ご自身のモデルを実装される際に参考としてご活用ください。
6.1. 予測対象の検討
5章でBERT特徴量の抽出を行いましたが、特徴量はニュース毎に取得できますので、毎週数千のニュースに対してそれぞれ特徴量が出力されることになります。まずは、この特徴量を活用して何を予測するか目的を決めます。
シンプルに次の週にどの銘柄が値上がりするかを予測できれば、手っ取り早く収益を上げることができそうです。ただし、各週の数千個のニュースを利用して、次の週に値上がりする銘柄を予測するには、ニュース数と銘柄数のバランスを考えても少し難しい課題になりそうです。また、本コンペティションの課題においては、購入原資産全てを銘柄購入に利用する必要はなく、一部は現金で保持できることに着目します。
マーケット全体が値下がりするときにすべての現金を銘柄購入に利用すると収益が低下する可能性があります。つまり、次の週にマーケットが下落することがわかれば、現金比率を高めることによって、マーケット全体の下落の影響を低減することができるはずです。実際に、マーケットの状況に応じて現金比率を操作する運用を実施するファンドも存在しています。
以上の考察から、ニュースから抽出した特徴量を利用する予測モデルの予測対象としては、投資対象のユニバースの週次の平均リターンとし、BERT特徴量から下落の予兆を検知した場合は、現金比率を上げるという手法を採用することにします。他にもセクター(33業種分類など)のリターンを予測し、値上がりが予想されるセクターの代表的な銘柄を購入するなど様々な手法が考えられます。
6.1.1. 可変な特徴量を扱う方法
各週で公表されるニュースの数は可変であるため、ニュースデータから毎週抽出できる特徴量の次元数も可変となります。一般的にモデル構築するときは投入する特徴量の次元数は固定化する必要がありますので、可変な特徴量を用いてモデルを設計する場合には工夫が必要です。例えば、以下のような方法が考えられます。
-
予測時点から直近X個のニュースを解析対象にすることで、特徴量の次元数を固定化する
-
特徴量をPCAなどの次元圧縮手法を用いて一つのスコアにする(5章で紹介した方法)
-
LSTMのような可変長の入力が可能なレイヤーを作る
本章では、学習時に目的関数を設定でき、特定の目的に特化したスコアを設計することができるLSTMを可変長入力が可能なレイヤーとして活用する方法を紹介します。
6.2. LSTMによる可変特徴量の統合処理
この節では、LSTMのモデル作成及び、学習の方法を説明し、最終的にBERT特徴量を単一な特徴量として抽出する方法を説明します。
6.2.1. BERT特徴量ロード
まずはBERT特徴量をロードします。BERT特徴量は5章でご自分で保存したもの、もしくは、 こちら からダウンロードしたものをご利用ください。
headline_features = pd.read_pickle(f'{CONFIG["base_path"]}/headline_features/headline_features.pkl')
keywords_features = pd.read_pickle(f'{CONFIG["base_path"]}/keywords_features/keywords_features.pkl')
# 確認する。
headline_features.head(3)
keywords_features.head(3)6.2.2. データのロード
LSTMの学習時に用いるラベル(投資対象のユニバースの平均の週次リターン)を作成するため、株の価格情報と銘柄情報をロードします。
# stock_priceとstock_listをロードします。
stock_price = pd.read_csv(CONFIG["stock_price_path"])
stock_list = pd.read_csv(CONFIG["stock_list_path"])
# 確認する
stock_price.head(3)
stock_list.head(3)stock_listから投資対象銘柄を取得します。
codes = stock_list[stock_list["universe_comp2"] == True][
"Local Code"
].values投資対象銘柄を使用してstock_priceの銘柄を絞り込みます。
stock_price = stock_price.loc[stock_price.loc[:, "Local Code"].isin(codes)]ロードしたデータの生成を行います。まず、stock_priceを扱いやすい形に変換します。データのうち ['EndOfDayQuote Date', 'Local Code', "EndOfDayQuote Open", "EndOfDayQuote ExchangeOfficialClose"] のcolumnをラベル作成のために使用します。
-
EndOfDayQuote Date: データの日付
-
Local Code: 銘柄コード
-
EndOfDayQuote Open: 始値
-
EndOfDayQuote ExchangeOfficialClose: 終値
stock_price = stock_price[['EndOfDayQuote Date', 'Local Code', "EndOfDayQuote Open", "EndOfDayQuote ExchangeOfficialClose"]]
# それぞれのcolumn名をわかりやすく変更する
stock_price = stock_price.rename(columns={
'EndOfDayQuote Date': 'date',
'Local Code': 'asset',
'EndOfDayQuote Open': 'open',
'EndOfDayQuote ExchangeOfficialClose': 'close',
})
# データごとにindex形式が異なると大変扱いにくい。下記のコードより特徴量と同様のindexの形式を変更する。
# pd.to_datetimeより、string形式の日付をpd.Timestamp形式に変換する
# pd.Timestamp形式をpd.DatetimeIndex形式に変更し、time zoneをheadline_featuresと同様に設定する。
# この際、headline_featuresとkeywords_featuresはarticlesのindexを使用しているため、timezoneが一致している。どちらを用いても良い。
stock_price['date'] = pd.to_datetime(stock_price['date'])
stock_price['date'] = pd.DatetimeIndex(stock_price['date']).tz_localize(headline_features.index.tz)
# indexを['date', 'asset']順のpd.MultiIndex形式として設定する。
stock_price = stock_price.set_index(['date', 'asset']).sort_index()
# unstack()より銘柄情報をcolumnに移動させる。
stock_price = stock_price.unstack()
# 今回使用するデータは2020年以降のデータであるので、2020年以前のデータを切り捨てる。
stock_price = stock_price['2020-01-01':]
# 確認する
display(stock_price.head())出力結果は以下の通りです。stock_priceを以下のような形式を持つように変更しました。
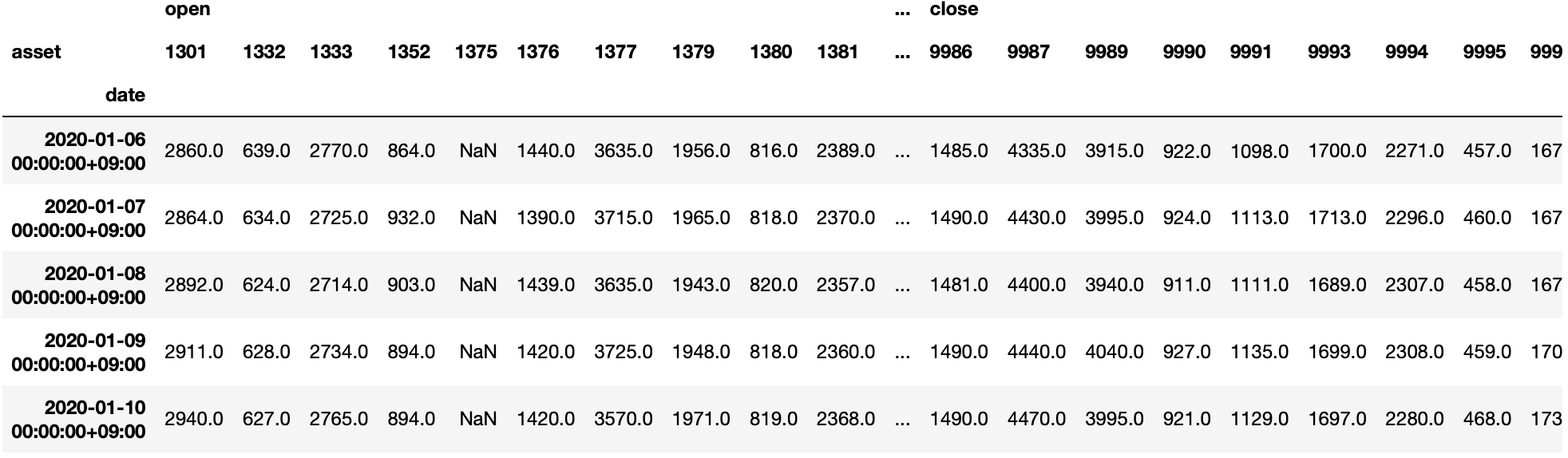
6.2.3. 週ごとにグループされた特徴量とラベルの作成
各週ごとの特徴量を統合するためには、週ごとの全ての特徴量をグループ化すると扱いやすくなります。ここでは、週ごとに特徴量と価格情報をグループ化する方法を説明します。また、週ごとの価格情報をグループ化し、週次の平均リターンを計算し、ラベルを作成する方法を説明します。
6.2.4. 本番提出用のクラスへ組み込み
SentimentGeneratorクラスに ""_build_weekly_group"" 関数を追加します。
@classmethod
def _build_weekly_group(cls, df):
# index情報から、(year, week)の情報を得る。
return pd.Series(list(zip(df.index.year, df.index.week)), index=df.index)
# SentimentGeneratorに定義したclassmethodを追加する
SentimentGenerator._build_weekly_group = _build_weekly_group
# 特徴量に適用してみる
display_markdown('#### features', raw=True)
features = headline_features
weekly_group = SentimentGenerator._build_weekly_group(df=features)
display(weekly_group.head(3))
display(weekly_group.tail(3))
# プライスに適用してみる。
# stock priceの2020年の1週目は、データが存在しないため、2020年の2週目から存在することがわかる。
# これらのindexをマッチさせる方法は後ほど説明する。
display_markdown('#### stock price', raw=True)
weekly_group = SentimentGenerator._build_weekly_group(stock_price)
display(weekly_group.head(3))
display(weekly_group.tail(3))出力結果は以下の通りです。
features
publish_datetime
2020-01-01 00:00:00+09:00 (2020, 1)
2020-01-01 00:00:00+09:00 (2020, 1)
2020-01-01 00:00:00+09:00 (2020, 1)
dtype: object
publish_datetime
2020-12-31 23:00:00+09:00 (2020, 53)
2020-12-31 23:12:31+09:00 (2020, 53)
2020-12-31 23:26:35+09:00 (2020, 53)
dtype: object
labels
index
2020-01-06 00:00:00-05:00 (2020, 2)
2020-01-07 00:00:00-05:00 (2020, 2)
2020-01-08 00:00:00-05:00 (2020, 2)
dtype: object
index
2021-01-27 00:00:00-05:00 (2021, 4)
2021-01-28 00:00:00-05:00 (2021, 4)
2021-01-29 00:00:00-05:00 (2021, 4)
dtype: object特徴量を週ごとにグループ化してみましょう。
weekly_group = SentimentGenerator._build_weekly_group(df=features)
features = features.groupby(weekly_group).apply(lambda x: x[:])
# 確認する
features.head(3)出力結果は以下の通りです。週の情報がindexのlevel0に付与され、グループ化されていることが分かります。

続いて、trainとtestを区切る週をboundary_weekとして設定し、train用に用いられる特徴量と、test用に用いられる特徴量を区切ります。boundry_weekは26とし、trainとtestを52週の半分、つまり、2020年前半のニュースを訓練用データ、2020年後半のニュースをテストデータとしています。
boundary_week = (2020, 26)
train_features = features[features.index.get_level_values(0) <= boundary_week]
test_features = features[features.index.get_level_values(0) > boundary_week]
display_markdown('#### train_features', raw=True)
display(train_features.head(3))
display(train_features.tail(3))
display_markdown('#### test_features', raw=True)
display(test_features.head(3))
display(test_features.tail(3))出力結果は以下の通りです。
ここでは、LSTMの学習に係るのラベルデータを作成するために、stock priceを週ごとにグループ化し、翌週の週初営業日の始値から週末営業日の終値にかけての平均リターンを作成する方法を説明します。まずは、当週の週初営業日の始値から週末営業日の終値にかけての平均リターンを作成してみましょう。週次の平均リターンを作成する関数を_compute_weekly_returnとして定義します。
def _compute_weekly_return(x):
# その週の初営業日のopenから最終営業日のcloseまでのリターンを計算する。
weekly_return = ((x['close'].iloc[-1] - x['open'].iloc[0]) / x['open'].iloc[0])
# その日のvolumneが0であるデータは、openが0となっている。
# openが0の場合、np.infの値となっているため、np.nanに変換し除去する。
# 銘柄ごとのリターンを単純平均し、marketのweekly_returnを計算する。
return weekly_return.replace([np.inf, -np.inf], np.nan).dropna().mean()
weekly_group = SentimentGenerator._build_weekly_group(df=stock_price)
weekly_return = stock_price.groupby(weekly_group).apply(_compute_weekly_return)
display(weekly_return.head(3))
display(weekly_return.tail(3))出力結果は以下の通りです。
(2020, 2) 0.017291
(2020, 3) -0.007994
(2020, 4) -0.005600
dtype: float64
(2020, 51) 0.001516
(2020, 52) -0.009117
(2020, 53) 0.005004
dtype: float64ここで、weekly_returnをshift(-1)することにより、翌週のreturn情報が現在のindexに入るようになります。
weekly_fwd_return = weekly_return.shift(-1).dropna()
# 確認する
display(weekly_fwd_return.head(3))
display(weekly_fwd_return.tail(3))出力結果は以下の通りです。
(2020, 2) -0.007994
(2020, 3) -0.005600
(2020, 4) -0.015110
dtype: float64
(2020, 50) 0.001516
(2020, 51) -0.009117
(2020, 52) 0.005004
dtype: float64ここで、ラベルデータを訓練期間/テスト期間に分割します。現在のデータは、2020年の第1週から第52週まであり、前半の第1週から第26週までを訓練期間、第27週から52週までをテスト期間とします。具体的には、訓練期間とテスト期間を区切る週を`boundary_week`として、訓練用に用いられる特徴量と、テスト用に用いられる特徴量を区切ります。
boundary_week = (2020, 26)
train_labels = weekly_fwd_return[weekly_fwd_return.index <= boundary_week]
test_labels = weekly_fwd_return[weekly_fwd_return.index > boundary_week]
display_markdown('#### train_labels', raw=True)
display(train_labels.head(3))
display(train_labels.tail(3))
display_markdown('#### test_labels', raw=True)
display(test_labels.head(3))
display(test_labels.tail(3))出力結果は以下の通りです。
train_labels
(2020, 2) -0.007994
(2020, 3) -0.005600
(2020, 4) -0.015110
dtype: float64
(2020, 24) 0.016623
(2020, 25) 0.001732
(2020, 26) -0.019522
dtype: float64
test_labels
(2020, 27) -0.017781
(2020, 28) 0.016613
(2020, 29) 0.001590
dtype: float64
(2020, 50) 0.001516
(2020, 51) -0.009117
(2020, 52) 0.005004
dtype: float64fwd_returnの上げ下げの情報のみをラベルとして用いるため、上げを1.0, 下げを0.0に変換します。
train_labels = (train_labels >= 0) * 1.0
test_labels = (test_labels >= 0) * 1.0
display_markdown('#### train_labels', raw=True)
display(train_labels.head(3))
display(train_labels.tail(3))
display_markdown('#### test_labels', raw=True)
display(test_labels.head(3))
display(test_labels.tail(3))出力結果は以下の通りです。うまく0.0と1.0に変換されています。
train_labels
(2020, 2) 0.0
(2020, 3) 0.0
(2020, 4) 0.0
dtype: float64
(2020, 24) 1.0
(2020, 25) 1.0
(2020, 26) 0.0
dtype: float64
test_labels
(2020, 27) 0.0
(2020, 28) 1.0
(2020, 29) 1.0
dtype: float64
(2020, 50) 1.0
(2020, 51) 0.0
(2020, 52) 1.0
dtype: float646.2.5. 本番提出用のクラスへ組み込み
上記のコードを関数として、SentimentGenerator クラスに追加します。
@classmethod
def build_weekly_features(cls, features, boundary_week):
assert isinstance(boundary_week, tuple)
weekly_group = cls._build_weekly_group(df=features)
features = features.groupby(weekly_group).apply(lambda x: x[:])
train_features = features[features.index.get_level_values(0) <= boundary_week]
test_features = features[features.index.get_level_values(0) > boundary_week]
return {'train': train_features, 'test': test_features}
@classmethod
def build_weekly_labels(cls, stock_price, boundary_week):
def _compute_weekly_return(x):
# その週の初営業日のopenから最終営業日のcloseまでのリターンを計算する。
weekly_return = ((x['close'].iloc[-1] - x['open'].iloc[0]) / x['open'].iloc[0])
# その日のvolumneが0であるデータは、openが0となっている。
# openが0の場合、np.infの値となっているため、np.nanに変換し除去する。
# 銘柄ごとのリターンを単純平均し、marketのweekly_returnを計算する。
return weekly_return.replace([np.inf, -np.inf], np.nan).dropna().mean()
assert isinstance(boundary_week, tuple)
weekly_group = cls._build_weekly_group(df=stock_price)
weekly_fwd_return = stock_price.groupby(weekly_group).apply(_compute_weekly_return).shift(-1).dropna()
train_labels = weekly_fwd_return[weekly_fwd_return.index <= boundary_week]
test_labels = weekly_fwd_return[weekly_fwd_return.index > boundary_week]
train_labels = (train_labels >= 0) * 1.0
test_labels = (test_labels >= 0) * 1.0
return {'train': train_labels, 'test': test_labels}
# SentimentGeneratorに定義したclassmethodを追加する
SentimentGenerator.build_weekly_features = build_weekly_features
SentimentGenerator.build_weekly_labels = build_weekly_labels
# SentimentGeneratorに定義したclassmethodを追加する
SentimentGenerator.build_weekly_features = build_weekly_features
SentimentGenerator.build_weekly_labels = build_weekly_labels6.2.6. Pytorch Dataset作成
pytorchを用いたモデルを効率よく学習させるためには、custom Datasetクラスと、それを用いたDataloaderを定義する必要があります。ここでは、学習で用いるDatasetを定義する方法を説明します。Datasetの__getitem__は、Dataloaderを介してデータを取得するときに呼ばれます。具体的には、__init__で事前に定義したデータをidを用いて取得する仕組みになっています。そのため、idが与えられたら、そのidからfeatureとlabelを取得するような構造で__init__でデータを事前に定義しておく必要があります。以下にPytorchのDataset及びDataLoaderに関する参考記事を少し紹介しています。
Pytorch関連記事 |
Qiita:pyTorchのtransforms,Datasets,Dataloaderの説明と自作Datasetの作成と使用 |
ここでは、例としてtrainデータのみを用いて、Datasetを作っています。任意に特徴量としては、headlineを使い、boundary_weekに2020年の26週目を設定します。
features = headline_features
boundary_week = (2020, 26)
# 上記で作成したコードを用いて週次の特徴量とラベルを作成
weekly_features = SentimentGenerator.build_weekly_features(features=features, boundary_week=boundary_week)['train']
weekly_labels = SentimentGenerator.build_weekly_labels(stock_price=stock_price, boundary_week=boundary_week)['train']
# 共通する週のみのデータを使うため、共通するindex情報を取得する。
mask_index = weekly_features.index.get_level_values(0).unique() & weekly_labels.index
display(mask_index)出力結果は以下の通りです。
Index([ (2020, 2), (2020, 3), (2020, 4), (2020, 5), (2020, 6), (2020, 7),
(2020, 8), (2020, 9), (2020, 10), (2020, 11), (2020, 12), (2020, 13),
(2020, 14), (2020, 15), (2020, 16), (2020, 17), (2020, 18), (2020, 19),
(2020, 20), (2020, 21), (2020, 22), (2020, 23), (2020, 24), (2020, 25),
(2020, 26)],
dtype='object')共通するindexのみのデータだけでreindexします。
weekly_features = weekly_features[weekly_features.index.get_level_values(0).isin(mask_index)]
weekly_labels = weekly_labels.reindex(mask_index)
display_markdown('#### weekly_features', raw=True)
display(weekly_features.head(3))
display(weekly_features.tail(3))
display_markdown('#### weekly_labels', raw=True)
display(weekly_labels.head(3))
display(weekly_labels.tail(3))出力結果は以下の通りです。

idからweekの情報を取得できるよう、id_to_weekを作成します。
id_to_week = {id: week for id, week in enumerate(sorted(weekly_labels.index))}
id_to_week出力結果は以下の通りです。
{0: (2020, 2),
1: (2020, 3),
2: (2020, 4),
3: (2020, 5),
4: (2020, 6),
5: (2020, 7),
6: (2020, 8),
7: (2020, 9),
8: (2020, 10),
9: (2020, 11),
10: (2020, 12),
11: (2020, 13),
12: (2020, 14),
13: (2020, 15),
14: (2020, 16),
15: (2020, 17),
16: (2020, 18),
17: (2020, 19),
18: (2020, 20),
19: (2020, 21),
20: (2020, 22),
21: (2020, 23),
22: (2020, 24),
23: (2020, 25),
24: (2020, 26)}_getitem_で付与されたidから、データを取得するロジックを説明します。
# 例として、任意的にid = 10を用いる。
id = 10
# idからweekの情報を取得する。
week = id_to_week[id]
# 学習時のリソース軽減のため、全ての特徴量を入力とするわけではなく、直近n個を入力とする。ここでは1000個として定義する。
max_sequence_length = 1000
x = weekly_features.xs(week, axis=0, level=0)[-max_sequence_length:]
y = weekly_labels[week]
# 上記のコードよりidが付与されたとき、idから週の情報を取得し、その週の情報から、特徴量とラベルを手にすることができた。
display_markdown('#### 特徴量', raw=True)
display(x.head(3))
print('shape:', x.shape)
display_markdown('#### ラベル', raw=True)
display(y)出力結果は以下の通りです。
pytorchを用いた学習・推論では、データをtorch.Tensorタイプとして扱うことが要求されます。以下で、np.ndarrayをtensor形式に変換することができます。
x = torch.tensor(x.values, dtype=torch.float)
y = torch.tensor(y, dtype=torch.float)
display(x)
display(y)出力結果は以下の通りです。
tensor([[-0.2525, 0.3046, -0.2245, ..., -0.4402, -0.2707, 0.2823],
[ 0.0670, 0.1914, -0.1088, ..., -0.0879, -0.2142, 0.1802],
[-0.2898, -0.3260, -0.1711, ..., -0.1327, -0.2654, 0.1255],
...,
[-0.2813, -0.0425, 0.0015, ..., -0.7122, 0.1824, -0.0727],
[-0.7515, 0.1514, -0.0536, ..., -0.5100, -0.3639, -0.2901],
[ 0.0920, 0.0485, -0.2583, ..., -0.3228, 0.3854, 0.0924]])
tensor(1.)今回、学習に用いる週次のデータセットにおいて、LSTMの学習には週毎のニュースの件数が若干不足している傾向にあることから、過学習防止のため、少し工夫をしています。具体的には、全体的な特徴量(ニュースの情報)の順序は維持しつつ複数に分割し、その分割の中でシャッフルを行う方法を取ります。この方法を用いることで、モデルに入力するデータを増やすことでき、過学習を防止に繋がる効果が期待できます。
def _shuffle_by_local_split(x, split_size=50):
return torch.cat([splitted[torch.randperm(splitted.size()[0])] for splitted in x.split(split_size, dim=0)], dim=0)
x = _shuffle_by_local_split(x=x)
display(x)出力結果は以下の通りです。
tensor([[-0.1477, 0.1549, -0.0650, ..., 0.0304, 0.0071, 0.3565],
[-0.2660, 0.6258, -0.1581, ..., -0.2906, -0.3727, 0.0437],
[-0.2384, -0.1165, -0.2715, ..., -0.3553, -0.6599, -0.1545],
...,
[-0.7515, 0.1514, -0.0536, ..., -0.5100, -0.3639, -0.2901],
[-0.1901, 0.2114, -0.2073, ..., -0.3650, -0.3166, 0.2325],
[-0.4610, 0.4689, -0.0572, ..., -0.2271, -0.2781, -0.1097]])学習中においては、データを1つずつ読み込んで学習を行うより、複数個を同時に並列演算を行う方(mini batch)が時間短縮に繋がります。そのためには、データ行列を重ねる必要があり、データのsequenceが同一である必要があります。本節では、このようなシークエンスの異なるデータを扱うため、max_sequence_lengthを決め、最大のsequenceに合わせます。また、sequenceがmax_sequence_lengthに達しない場合は、前から0を埋め(zero padding)、sequenceを合わせています。なお、本節ではmax_sequence_lengthは1000と定義してあります。
# sequenceがmax_sequence_lengthに達しないrandomのtensorをxとして、定義し、以下のコードでzero paddingを行ってみる。
x = torch.randn(100, 768)
display_markdown('#### Padding前', raw=True)
display(x)
display(x.shape)
if x.size()[0] < max_sequence_length:
x = F.pad(x, pad=(0, 0, max_sequence_length - x.size()[0], 0))
display_markdown('#### Padding後', raw=True)
display(x)
display(x.shape)出力結果は以下の通りです。
Padding前
tensor([[-0.0767, 1.8950, -0.9323, ..., 0.1885, -1.3335, 0.3923],
[-0.5709, 0.4231, 0.4268, ..., -0.8555, -0.6662, -0.0097],
[ 0.3191, -0.3961, -0.9253, ..., -1.0401, 0.4225, -0.2478],
...,
[-0.0769, -0.0747, -0.2437, ..., 0.3740, 0.0970, 0.6437],
[ 1.1534, 0.8583, 1.2623, ..., 0.0882, 0.5125, -0.1485],
[ 2.1272, 0.8173, 0.8997, ..., -0.5132, 0.5023, 0.3106]])
torch.Size([100, 768])
Padding後
tensor([[ 0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],
...,
[-0.0769, -0.0747, -0.2437, ..., 0.3740, 0.0970, 0.6437],
[ 1.1534, 0.8583, 1.2623, ..., 0.0882, 0.5125, -0.1485],
[ 2.1272, 0.8173, 0.8997, ..., -0.5132, 0.5023, 0.3106]])
torch.Size([1000, 768])上記のコードをまとめて、pytorchのDatasetクラスを作成します。
class Dataset(_Dataset):
def __init__(self, weekly_features, weekly_labels, max_sequence_length):
# 共通する週のみを使うため、共通するindex情報を取得する
mask_index = (
weekly_features.index.get_level_values(0).unique() & weekly_labels.index
)
# 共通するindexのみのデータだけでreindexを行う。
self.weekly_features = weekly_features[
weekly_features.index.get_level_values(0).isin(mask_index)
]
self.weekly_labels = weekly_labels.reindex(mask_index)
# idからweekの情報を取得できるよう、id_to_weekをビルドする
self.id_to_week = {
id: week for id, week in enumerate(sorted(weekly_labels.index))
}
self.max_sequence_length = max_sequence_length
def _shuffle_by_local_split(self, x, split_size=50):
return torch.cat(
[
splitted[torch.randperm(splitted.size()[0])]
for splitted in x.split(split_size, dim=0)
],
dim=0,
)
def __len__(self):
return len(self.weekly_labels)
def __getitem__(self, id):
# 付与されたidから週の情報を取得し、その週の情報から、特徴量とラベルを取得する。
week = self.id_to_week[id]
x = self.weekly_features.xs(week, axis=0, level=0)[-self.max_sequence_length :]
y = self.weekly_labels[week]
# pytorchでは、データをtorch.Tensorタイプとして扱うことが要求される。
# 全体的な特徴量(ニュースの情報)の順序は維持しつつ、入力とする特徴量を数分割し、その分割の中でシャッフルを行う。
x = self._shuffle_by_local_split(torch.tensor(x.values, dtype=torch.float))
y = torch.tensor(y, dtype=torch.float)
# max_sequence_lengthに最大のsequenceを合わせ、sequenceがmax_sequence_lengthに達しない場合は、前から0を埋め、sequenceを合わせる
if x.size()[0] < self.max_sequence_length:
x = F.pad(x, pad=(0, 0, self.max_sequence_length - x.size()[0], 0))
return x, y6.2.7. LSTMによる特徴量合成モデル作成
LSTMを用いて上げ下げの確率を出力とするモデルを定義し、binary_cross_entropyを損失関数として学習を行います。モデルへの入力Sequenceがかなり長いため、入力の最初の方の情報の消失が激しいと想定されます。そのため今回は、LSTMにおいて bidirectional を利用しています。具体的なLSTMの定義は以下のソースコードを確認してください。出力層でのsentiment score(上げ下げの情報)及び出力の直前の層の高次元の情報を抽出し、特徴量として用いることを想定しています。
class FeatureCombiner(nn.Module):
def __init__(self, input_size, hidden_size, compress_dim=4, num_layers=2):
super().__init__()
self.input_size = input_size
self.hidden_size = hidden_size
# LSTMの定義
# batch_firstより、出力次元の最初がbatchとなる。
# dropoutを用いて、内部状態のconnectionをdropすることより過学習を防ぐ。
# Sequenceがかなり長く、入力の始めの方の情報の消失を防ぐため、bidirectionalのモデルを使う。
self.cell = nn.LSTM(
input_size=input_size,
hidden_size=hidden_size,
num_layers=num_layers,
batch_first=True,
dropout=0.5,
bidirectional=True,
)
# より高次元の特徴量を抽出できるようにするため、classifierの手前で、compress_dim次元への線形圧縮を行う。
self.compressor = nn.Linear(hidden_size * 2, compress_dim)
# sentiment probabilityの出力層。
self.classifier = nn.Linear(compress_dim, 1)
# outputの範囲を[0, 1]とする。
self.sigmoid = nn.Sigmoid()
def forward(self, x):
# 入力値xから出力までの流れを定義する。
output, _ = self.cell(x)
output = self.sigmoid(self.classifier(self.compressor(output[:, -1, :])))
return output
def extract_feature(self, x):
# 入力値xから特徴量抽出までの流れを定義する。
output, _ = self.cell(x)
output = self.compressor(output[:, -1, :])
return output6.2.8. 特徴量合成モデルのハンドラー作成
前節において、データのインデクシングロジックや、特徴量合成モデルは作成しました。しかし、これらだけではモデル学習は行えません。学習のロジックや、学習されたモデルのセーブ及びロード、推定、特徴量抽出を実装する必要があります。本節では、これらを実装するためにFeatureCombinerHandlerのクラスを定義しています。
class FeatureCombinerHandler:
def __init__(self, feature_combiner_params, store_dir):
# モデル学習及び推論に用いるデバイスを定義する
if torch.cuda.device_count() >= 1:
self.device = 'cuda'
print("[+] Set Device: GPU")
else:
self.device = 'cpu'
print("[+] Set Device: CPU")
# モデルのcheckpointや抽出した特徴量及びsentimentをstoreする場所を定義する。
self.store_dir = store_dir
os.makedirs(store_dir, exist_ok=True)
# 上記で作成したfeaturecombinerを定義する。
self.feature_combiner = FeatureCombiner(**feature_combiner_params).to(
self.device
)
# 学習に用いるoptimizerを定義する。
self.optimizer = torch.optim.Adam(
params=self.feature_combiner.parameters(), lr=0.001,
)
# ロス関数の定義
self.criterion = nn.BCELoss().to(self.device)
# モデルのcheck pointが存在する場合、モデルをロードする
self._load_model()
# 学習に必要なデータ(並列のためbatch化されたもの)をサンプルする。
def _sample_xy(self, data_type):
assert data_type in ("train", "val")
# data_typeより、data_typeに合致したデータを取得するようにしている。
if data_type == "train":
# dataloaderをiteratorとして定義し、next関数として毎時のデータをサンプルすることができる。
# Iteratorは全てのデータがサンプルされると、StopIterationのエラーを発するが、そのようなエラーが出たとき、
# Iteratorを再定義し、データをサンプルするようにしている。
try:
x, y = next(self.iterable_train_dataloader)
except StopIteration:
self.iterable_train_dataloader = iter(self.train_dataloader)
x, y = next(self.iterable_train_dataloader)
elif data_type == "val":
try:
x, y = next(self.iterable_val_dataloader)
except StopIteration:
self.iterable_val_dataloader = iter(self.val_dataloader)
x, y = next(self.iterable_val_dataloader)
return x.to(self.device), y.to(self.device)
# モデルのパラメータをアップデートするロジック
def _update_params(self, loss):
# ロスから、gradientを逆伝播し、パラメータをアップデートする
loss.backward()
self.optimizer.step()
# 学習されたfeature_combinerのパラメータをcheck_pointとしてstoreするロジック
def _save_model(self, epoch):
torch.save(
self.feature_combiner.state_dict(),
os.path.join(self.store_dir, f"{epoch}.ckpt"),
)
print(f"[+] Epoch: {epoch}, Model is saved.")
# 学習されたcheckpointが存在す場合、feature_combinerにそのパラメータをロードするロジック
def _load_model(self):
# cudaで学習されたモデルなどを、cpu環境下でロードするときはこのパラメータが必要となる。
params_to_load = {}
if self.device == "cpu":
params_to_load["map_location"] = torch.device("cpu")
# .ckptファイルを探し、古い順から新しい順にソートする。
check_points = glob(os.path.join(self.store_dir, "*.ckpt"))
check_points = sorted(
check_points, key=lambda x: int(x.split("/")[-1].replace(".ckpt", "")),
)
# check_pointが存在しない場合は、スキップする。
if len(check_points) == 0:
print("[!] No exists checkpoint")
return
# 複数個のchieck_pointが存在する場合、一番最新のものを使い、モデルのパラメータをロードする
check_point = check_points[-1]
self.feature_combiner.load_state_dict(torch.load(check_point, **params_to_load))
print("[+] Model is loaded")
# Datasetからdataloaderを定義するロジック
def _build_dataloader(
self, dataloader_params, weekly_features, weekly_labels, max_sequence_length
):
# 上記3で作成したしたdatasetを定義する
dataset = Dataset(
weekly_features=weekly_features,
weekly_labels=weekly_labels,
max_sequence_length=max_sequence_length,
)
# datasetのdataをiterableにロードできるよう、dataloaderを定義する、このとき、shuffle=Trueを渡すことで、データはランダムにサンプルされるようになる。
return DataLoader(dataset=dataset, shuffle=True, **dataloader_params)
# train用に、featuresとlabelsを渡し、datasetを定義し、dataloaderを定義するロジック
def set_train_dataloader(
self, dataloader_params, weekly_features, weekly_labels, max_sequence_length
):
self.train_dataloader = self._build_dataloader(
dataloader_params=dataloader_params,
weekly_features=weekly_features,
weekly_labels=weekly_labels,
max_sequence_length=max_sequence_length,
)
# dataloaderからiteratorを定義する
# iteratorはnext関数よりデータをサンプルすることが可能となる。
self.iterable_train_dataloader = iter(self.train_dataloader)
# validation用に、featuresとlabelsを渡し、datasetを定義し、dataloaderを定義するロジック
def set_val_dataloader(
self, dataloader_params, weekly_features, weekly_labels, max_sequence_length
):
self.val_dataloader = self._build_dataloader(
dataloader_params=dataloader_params,
weekly_features=weekly_features,
weekly_labels=weekly_labels,
max_sequence_length=max_sequence_length,
)
# dataloaderからiteratorを定義する
# iteratorはnext関数よりデータをサンプルすることが可能となる。
self.iterable_val_dataloader = iter(self.val_dataloader)
# 学習ロジック
def train(self, n_epoch):
# n_epochの回数分、全学習データを複数回用いて学習する。
for epoch in range(n_epoch):
# 各々のepochごとのaverage lossを表示するため、lossをstoreするリストを定義する。
train_losses = []
test_losses = []
# train_dataloaderの長さは、全ての学習データを一度用いるときの長さと同様である。
# batchを組むと、その分train_dataloaderの長さは可変し、ちょうど一度全てのデータで学習できる長さを返す。
for iter_ in tqdm(range(len(self.train_dataloader))):
# パラメータをtrainableにするため、feature_combinerをtrainモードにする。
self.feature_combiner.train()
# trainデータをサンプルする。
x, y = self._sample_xy(data_type="train")
# feature_combinerに特徴量を入力し、sentiment scoreを取得する。
preds = self.feature_combiner(x=x)
# sentiment scoreとラベルとのロスを計算する。
train_loss = self.criterion(preds, y.view(-1, 1))
# 計算されたロスは、後ほどepochごとのdisplayに使用するため、storeしておく。
train_losses.append(train_loss.detach().cpu())
# lossから、gradientを逆伝播させ、パラメータをupdateする。
self._update_params(loss=train_loss)
# validation用のロースを計算する。
# 毎回計算を行うとコストがかかってくるので、iter_毎5回ごとに計算を行う。
if iter_ % 5 == 0:
# 学習を行わないため、feature_combinerをevalモードにしておく。
# evalモードでは、dropoutの影響を受けない。
self.feature_combiner.eval()
# 各パラメータごとのgradientを計算するとリソースが高まる。
# evaluationの時には、gradient情報を持たせないことで、メモリーの節約に繋がる。
with torch.no_grad():
# validationデータをサンプルする
x, y = self._sample_xy(data_type="val")
# feature_combinerに特徴量を入力し、sentiment scoreを取得する。
preds = self.feature_combiner(x=x)
# sentiment scoreとラベルとのロスを計算する。
test_loss = self.criterion(preds, y.view(-1, 1))
# 計算されたロスは、後ほどepochごとのdisplayに使用するため、storeしておく。
test_losses.append(test_loss.detach().cpu())
# 毎epoch終了後、平均のロスをプリントする。
print(
f"epoch: {epoch}, train_loss: {np.mean(train_losses):.4f}, val_loss: {np.mean(test_losses):.4f}"
)
# 毎epoch終了後、モデルのパラメータをstoreする。
self._save_model(epoch=epoch)
# 特徴量から、合成特徴量を抽出するロジック
def combine_features(self, features):
# 学習を行わないため、feature_combinerをevalモードにしておく。
self.feature_combiner.eval()
# gradient情報を持たせないことで、メモリーの節約する。
with torch.no_grad():
# 特徴量をfeature_combinerのextract_feature関数に入力し、出力層手前の特徴量を抽出する。
# 抽出するとき、tensorをcpu上に落とし、np.ndarray形式に変換する。
return (
self.feature_combiner.extract_feature(
x=torch.tensor(features, dtype=torch.float).to(self.device)
)
.cpu()
.numpy()
)
# 特徴量から、翌週のsentimentを予測するロジック
def predict_sentiment(self, features):
# 学習を行わないため、feature_combinerをevalモードにしておく。
self.feature_combiner.eval()
# gradient情報を持たせないことで、メモリーの節約する。
with torch.no_grad():
# 特徴量をfeature_combinerに入力し、sentiment scoreを抽出する。
# 抽出するとき、tensorをcpu上に落とし、np.ndarray形式に変換する。
return (
self.feature_combiner(x=torch.tensor(features, dtype=torch.float).to(self.device))
.cpu()
.numpy()
)
# weeklyグループされた特徴量を入力に、合成特徴量もしくは、sentiment scoreを抽出するロジック
def generate_by_weekly_features(
self, weekly_features, generate_target, max_sequence_length
):
assert generate_target in ("features", "sentiment")
generate_func = getattr(
self,
{"features": "combine_features", "sentiment": "predict_sentiment"}[
generate_target
],
)
# グループごとに特徴量もしくは、sentiment scoreを抽出し、最終的に重ねて返すため、リストを作成する。
outputs = []
# ユニークな週indexを取得する。
weeks = sorted(weekly_features.index.get_level_values(0).unique())
for week in tqdm(weeks):
# 各週ごとの特徴量を取得し、直近から、max_sequence_length分切る。
features = weekly_features.xs(week, axis=0, level=0)[-max_sequence_length:]
# 特徴量をモデルに入力し、合成特徴量もしくは、sentiment scoreを抽出し、outputsにappendする。
# np.expand_dims(features, axis=0)を用いる理由は、特徴量合成機の入力期待値は、dimention0がbatchであるが、
# featuresは、[1000, 768]の次元をもち、これらをunsqueezeし、[1, 1000, 768]に変換する必要がある。
outputs.append(generate_func(features=np.expand_dims(features, axis=0)))
# outputsを重ね、indexの情報とともにpd.DataFrame形式として返す。
return pd.DataFrame(np.concatenate(outputs, axis=0), index=weeks)6.2.9. 特徴量合成モデルの学習及び特徴量合成
本節では、実際作成したコードを元に、特徴量合成機の学習を行います。さらに、学習されたモデルを用いて、特徴量とsentiment scoreを抽出します。本実装では、モデルの過学習を防止するため、二つのランダム性を与えています。これは、学習のたびに異なるランダム性を与えられ、学習の再現は不可能となります。
学習における再現可能性を重要視する場合、ランダム性を固定する必要があります。しかし、本実装においては二つのランダム性を同時に固定しないといけないことから、そのための実装を実施するとコードの難易度が高まってしまいます。以上のことから、本チュートリアルではランダム性の固定を省略しています。学習の実行毎に少し異なるモデルが構築されることに留意しましょう。ただし、推論処理においてはここで固定化しなかったランダム性の影響はありませんので、同一のモデルを利用する限りは同一の予測結果が取得されます。推論処理の再現可能性はバックテスト評価において重要です。
まずは、上記で作成したFeatureCombinerHandlerをインスタンス化します。そのとき、feature_combiner_paramsに{"input_size": 768, "hidden_size": 128}を渡していますが、これはBERTから抽出した特徴量のサイズが768であるためです。LSTMが持つ内部状態のパラメータの次元においては、適切な値を設定しましょう。ここでは、128次元と設置しているのですが、過学習の恐れが高いときやパラメータを減らしても十分学習可能な時には、より低い値をセットしてみましょう。
feature_combiner_handler = FeatureCombinerHandler(feature_combiner_params={"input_size": 768, "hidden_size": 128}, store_dir=f'{CONFIG["base_path"]}/test')続いて、学習用とvalidation用のデータを構築します。一般的に、データは学習に用いられるTrainデータと、パラメータなどの調整のため用いられるvalidationデータ、学習後のモデルを評価するためのtestデータに分けることが多いですが、本チュートリアルでは、LSTMを十分に学習するにはデータ数が少ないため、TrainとTestデータに分割し、validation lossの算出時にもtestデータを用います。まずは、上記で作成したbuild_weekly_featuresとbuild_weekly_labelsを用いて、データセットを生成します。
boundary_week = (2020, 26)
weekly_features = SentimentGenerator.build_weekly_features(features, boundary_week)
weekly_labels = SentimentGenerator.build_weekly_labels(stock_price, boundary_week)学習を行う前に、データのサンプル及び、batch処理を行ってくれるDataloaderをビルドする必要があります。このとき、batch_sizeを4にすることで、4つのデータを並列に学習し、num_workersを2にすることでdataloaderはcpu 2coreを用いて、並列的に読み込まれます。max_sequence_lengthを1,000にすることで、学習中には1,000個のsequenceをmaxとして入力します。
# train dataloaderをsetする。
feature_combiner_handler.set_train_dataloader(
dataloader_params={
"batch_size": 4,
"num_workers": 2,
},
weekly_features=weekly_features['train'],
weekly_labels=weekly_labels['train'],
max_sequence_length=1000
)
# validation dataloaderをsetする。
feature_combiner_handler.set_val_dataloader(
dataloader_params={
"batch_size": 4,
"num_workers": 2,
},
weekly_features=weekly_features['test'],
weekly_labels=weekly_labels['test'],
max_sequence_length=1000
)学習を行ってみましょう。n_epochは全てのデータを一度用いた学習回数を表し、ここでは、テストであるため1と設定しています。
feature_combiner_handler.train(n_epoch=1)出力結果は以下の通りです。
epoch: 0, train_loss: 0.7934, val_loss: 0.6816
[+] Epoch: 0, Model is saved.学習後、特徴量抽出機から、特徴量やsentiment scoreを抽出することができます。今回は、一度学習されたモデルをロードし、特徴量とsentiment scoreを抽出してみます。上で定義した、feature_combiner_handlerを同様に定義すると、check_pointを探し、モデルがロードされます。
feature_combiner_handler = FeatureCombinerHandler(feature_combiner_params={"input_size": 768, "hidden_size": 128}, store_dir=f'{CONFIG["base_path"]}/test')sentiment scoreは以下のように取得できます。max_sequence_lengthは学習時と同様に、直近から利用する特徴量の最大の数を決めることができますが、評価時には、十分長い(全部かほぼ全部)の特徴量を合成するため、10,000を与えます。
sentiment_score = feature_combiner_handler.generate_by_weekly_features(weekly_features=weekly_features['test'], generate_target='sentiment', max_sequence_length=10000)
display(sentiment_score.head(3))
display(sentiment_score.tail(3))出力結果は以下の通りです。
また、より高次元の特徴量は以下のように取得できます。
combined_features = feature_combiner_handler.generate_by_weekly_features(weekly_features=weekly_features['test'], generate_target='features', max_sequence_length=10000)
display(combined_features.head(3))
display(combined_features.tail(3))出力結果は以下の通りです。
上で作成したFeatureCombinerHandlerは、本番環境においても特徴量の合成時に用います。SentimentGenerator クラスに、インスタンスとしてビルドしておきましょう。
SentimentGenerator.headline_feature_combiner_handler = FeatureCombinerHandler(feature_combiner_params={"input_size": 768, "hidden_size": 128}, store_dir=f'{CONFIG["base_path"]}/headline_features')
SentimentGenerator.keywords_feature_combiner_handler = FeatureCombinerHandler(feature_combiner_params={"input_size": 768, "hidden_size": 128}, store_dir=f'{CONFIG["base_path"]}/keywords_features')上記のコードをまとめ、headlineとkeywordsそれぞれにおいて、特徴量合成機を学習し、特徴量を抽出するコードを作成します。
boundary_week = (2020, 26)
for features, feature_type in [(headline_features, 'headline_features'), (keywords_features, 'keywords_features')]:
# feature_typeに合致するfeature_combiner_handlerをSentimentGeneratorから取得する。
feature_combiner_handler = {
'headline_features': SentimentGenerator.headline_feature_combiner_handler,
'keywords_features': SentimentGenerator.keywords_feature_combiner_handler,
}[feature_type]
# 学習及び、validationに用いる、データをビルドする
weekly_features = SentimentGenerator.build_weekly_features(features, boundary_week)
weekly_labels = SentimentGenerator.build_weekly_labels(stock_price, boundary_week)
# train dataloaderをsetする。
# このとき、batch_sizeを4にすることで、4つのデータを並列に学習し、
# num_workersを2にすることでdataloaderはcpu 2coreを用いて、並列的にロードされる。
feature_combiner_handler.set_train_dataloader(
dataloader_params={
"batch_size": 4,
"num_workers": 2,
},
weekly_features=weekly_features['train'],
weekly_labels=weekly_labels['train'],
max_sequence_length=1000
)
# validation dataloaderをsetする。
feature_combiner_handler.set_val_dataloader(
dataloader_params={
"batch_size": 4,
"num_workers": 2,
},
weekly_features=weekly_features['test'],
weekly_labels=weekly_labels['test'],
max_sequence_length=1000
)
# 学習
feature_combiner_handler.train(n_epoch=20)
# 特徴量及びsentiment scoreを抽出し、pickleとしてstoreする。
feature_combiner_handler.generate_by_weekly_features(weekly_features=weekly_features['test'], generate_target='sentiment', max_sequence_length=10000).to_pickle(os.path.join(f'{CONFIG["base_path"]}/{feature_type}', 'LSTM_sentiment.pkl'))
feature_combiner_handler.generate_by_weekly_features(weekly_features=weekly_features['test'], generate_target='features', max_sequence_length=10000).to_pickle(os.path.join(f'{CONFIG["base_path"]}/{feature_type}', 'LSTM_features.pkl'))6.2.10. 本番提出用のクラス作成
ここまでの、ニュースデータの読み込み、前処理、BERT特徴量、LSTMによる特徴量合成までの一連の処理を generate_lstm_features 関数として、SentimentGeneratorクラスに追加します。
@classmethod
def generate_lstm_features(
cls,
article_path,
start_dt=None,
boundary_week=(2020, 26),
target_feature_types=None,
):
# target_feature_typesが指定されなかったらデフォルト値設定
dfault_target_feature_types = [
"headline",
"keywords",
]
if target_feature_types is None:
target_feature_types = dfault_target_feature_types
# feature typeが想定通りであることを確認
assert set(target_feature_types).issubset(dfault_target_feature_types)
# ニュースデータをロードする。
articles = cls.load_articles(start_dt=start_dt, path=article_path)
# 前処理を行う。
articles = cls.normalize_articles(articles)
articles = cls.handle_punctuations_in_articles(articles)
articles = cls.drop_remove_list_words(articles)
# headlineとkeywordsの特徴量をdict型で返す。
lstm_features = {}
for feature_type in target_feature_types:
# コーパス全体のBERT特徴量を抽出する。
features = cls.generate_features_by_texts(texts=articles[feature_type])
# feature_typeに合致するfeature_combiner_handlerをclsから取得する。
feature_combiner_handler = {
"headline": cls.headline_feature_combiner_handler,
"keywords": cls.keywords_feature_combiner_handler,
}[feature_type]
# 特徴量を週毎のグループ化する。
weekly_features = cls.build_weekly_features(features, boundary_week)["test"]
# Sentiment scoreを抽出する。
lstm_features[
f"{feature_type}_features"
] = feature_combiner_handler.generate_by_weekly_features(
weekly_features=weekly_features,
generate_target="sentiment",
max_sequence_length=10000,
)
return lstm_features ここまでSentimentGeneratorに追加したclass methodをまとめ、SentimentGeneratorクラスを仕上げます。5章で実装した処理も一部利用してることに注意してください。
class SentimentGenerator(object):
article_columns = None
device = None
feature_extractor = None
headline_feature_combiner_handler = None
keywords_feature_combiner_handler = None
punctuation_replace_dict = None
punctuation_remove_list = None
@classmethod
def initialize(cls, base_dir="../model"):
# 使用するcolumnをセットする。
cls.article_columns = ["publish_datetime", "headline", "keywords"]
# BERT特徴量抽出機をセットする。
cls._set_device()
cls._build_feature_extractor()
cls._build_tokenizer()
# LSTM特徴量合成機をセットする。
cls.headline_feature_combiner_handler = FeatureCombinerHandler(
feature_combiner_params={"input_size": 768, "hidden_size": 128},
store_dir=f"{base_dir}/headline_features",
)
cls.keywords_feature_combiner_handler = FeatureCombinerHandler(
feature_combiner_params={"input_size": 768, "hidden_size": 128},
store_dir=f"{base_dir}/keywords_features",
)
# 置換すべき記号のdictionaryを作成する。
JISx0208_replace_dict = {
"髙": "高",
"﨑": "崎",
"濵": "浜",
"賴": "頼",
"瀨": "瀬",
"德": "徳",
"蓜": "配",
"昻": "昂",
"桒": "桑",
"栁": "柳",
"犾": "犹",
"琪": "棋",
"裵": "裴",
"魲": "鱸",
"羽": "羽",
"焏": "丞",
"祥": "祥",
"曻": "昇",
"敎": "教",
"澈": "徹",
"曺": "曹",
"黑": "黒",
"塚": "塚",
"閒": "間",
"彅": "薙",
"匤": "匡",
"冝": "宜",
"埇": "甬",
"鮏": "鮭",
"伹": "但",
"杦": "杉",
"罇": "樽",
"柀": "披",
"﨤": "返",
"寬": "寛",
"神": "神",
"福": "福",
"礼": "礼",
"贒": "賢",
"逸": "逸",
"隆": "隆",
"靑": "青",
"飯": "飯",
"飼": "飼",
"緖": "緒",
"埈": "峻",
}
cls.punctuation_replace_dict = {
**JISx0208_replace_dict,
"《": "〈",
"》": "〉",
"『": "「",
"』": "」",
"“": '"',
"!!": "!",
"〔": "[",
"〕": "]",
"χ": "x",
}
# 取り除く記号リスト。
cls.punctuation_remove_list = [
"|",
"■",
"◆",
"●",
"★",
"☆",
"♪",
"〃",
"△",
"○",
"□",
]
@classmethod
def _set_device(cls):
# 使用可能なgpuがある場合、そちらを利用し特徴量抽出を行う
if torch.cuda.device_count() >= 1:
cls.device = "cuda"
print("[+] Set Device: GPU")
else:
cls.device = "cpu"
print("[+] Set Device: CPU")
@classmethod
def _build_feature_extractor(cls):
# 特徴量抽出のため事前学習済みBERTモデルを用いる。
# ここでは、"cl-tohoku/bert-base-japanese-whole-word-masking"モデルを使用しているが、異なる日本語BERTモデルを用いても良い。
cls.feature_extractor = transformers.BertModel.from_pretrained(
"cl-tohoku/bert-base-japanese-whole-word-masking",
return_dict=True,
output_hidden_states=True,
)
# 使用するdeviceを指定
cls.feature_extractor = cls.feature_extractor.to(cls.device)
# 今回、学習は行わない。特徴量抽出のためなので、評価モードにセットする。
cls.feature_extractor.eval()
print("[+] Built feature extractor")
@classmethod
def _build_tokenizer(cls):
# BERTモデルの入力とするコーパスはそのBERTモデルが学習された時と同様の前処理を行う必要がある。
# 今回使用する"cl-tohoku/bert-base-japanese-whole-word-masking"モデルは、mecab-ipadic-NEologdによりトークナイズされ、その後Wordpiece subword encoderよりsubword化している。
# Subwordとは形態素の類似な概念として、単語をより小さい意味のある単位に変換したものである。
# transformersのBertJapaneseTokenizerは、その事前学習モデルの学習時と同様の前処理を簡単に使用することができる。
# この章ではBertJapaneseTokenizerを利用し、トークナイズ及びsubword化を行う。
cls.bert_tokenizer = BertJapaneseTokenizer.from_pretrained(
"cl-tohoku/bert-base-japanese-whole-word-masking"
)
print("[+] Built bert tokenizer")
@classmethod
def load_articles(cls, path, start_dt=None, end_dt=None):
# csvをロードする
# headline、keywordsをcolumnとして使用。publish_datetimeをindexとして使用。
articles = pd.read_csv(path)[cls.article_columns].set_index("publish_datetime")
# str形式のdatetimeをpd.Timestamp形式に変換
articles.index = pd.to_datetime(articles.index)
# NaN値を取り除く
articles = articles.dropna()
# 必要な場合、使用するデータの範囲を指定する
return articles[start_dt:end_dt]
@classmethod
def normalize_articles(cls, articles):
articles = articles.copy()
# 欠損値を取り除く
articles = articles.dropna()
for column in articles.columns:
# スペース(全角スペースを含む)はneologdn正規化時に全て除去される。
# ここでは、スペースの情報が失われないように、スペースを全て改行に書き換え、正規化後スペースに再変換する。
articles[column] = articles[column].apply(lambda x: "\n".join(x.split()))
# neologdnを使って正規化を行う。
articles[column] = articles[column].apply(lambda x: neologdn.normalize(x))
# 改行をスペースに置換する。
articles[column] = articles[column].str.replace("\n", " ")
return articles
@classmethod
def handle_punctuations_in_articles(cls, articles):
articles = articles.copy()
for column in articles.columns:
# punctuation_remove_listに含まれる記号を除去する
articles[column] = articles[column].str.replace(
fr"[{''.join(cls.punctuation_remove_list)}]", ""
)
# punctuation_replace_dictに含まれる記号を置換する
for replace_base, replace_target in cls.punctuation_replace_dict.items():
articles[column] = articles[column].str.replace(
replace_base, replace_target
)
# unicode正規化を行う
articles[column] = articles[column].apply(
lambda x: unicodedata.normalize("NFKC", x)
)
return articles
@classmethod
def drop_remove_list_words(cls, articles, remove_list_words=["人事"]):
articles = articles.copy()
for remove_list_word in remove_list_words:
# headlineもしくは、keywordsどちらかでremove_list_wordを含むニュース記事のindexマスクを作成。
drop_mask = articles["headline"].str.contains(remove_list_word) | articles[
"keywords"
].str.contains(remove_list_word)
# remove_list_wordを含まないニュースだけに精製する。
articles = articles[~drop_mask]
return articles
@classmethod
def build_inputs(cls, texts, max_length=512):
input_ids = []
token_type_ids = []
attention_mask = []
for text in texts:
encoded = cls.bert_tokenizer.encode_plus(
text,
None,
add_special_tokens=True,
max_length=max_length,
padding="max_length",
return_token_type_ids=True,
truncation=True,
)
input_ids.append(encoded["input_ids"])
token_type_ids.append(encoded["token_type_ids"])
attention_mask.append(encoded["attention_mask"])
# torchモデルに入力するためにはtensor形式に変え、deviceを指定する必要がある。
input_ids = torch.tensor(input_ids, dtype=torch.long).to(cls.device)
token_type_ids = torch.tensor(token_type_ids, dtype=torch.long).to(cls.device)
attention_mask = torch.tensor(attention_mask, dtype=torch.long).to(cls.device)
return input_ids, token_type_ids, attention_mask
@classmethod
def generate_features(cls, input_ids, token_type_ids, attention_mask):
output = cls.feature_extractor(
input_ids=input_ids,
token_type_ids=token_type_ids,
attention_mask=attention_mask,
)
features = output["hidden_states"][-2].mean(dim=1).cpu().detach().numpy()
return features
@classmethod
def generate_features_by_texts(cls, texts, batch_size=2, max_length=512):
n_batch = math.ceil(len(texts) / batch_size)
features = []
for idx in tqdm(range(n_batch)):
input_ids, token_type_ids, attention_mask = cls.build_inputs(
texts=texts[batch_size * idx : batch_size * (idx + 1)],
max_length=max_length,
)
features.append(
cls.generate_features(
input_ids=input_ids,
token_type_ids=token_type_ids,
attention_mask=attention_mask,
)
)
features = np.concatenate(features, axis=0)
# 抽出した特徴量はnp.ndarray形式となっており、これらは、日付の情報を失っているため、pd.DataFrame形式に変換する。
return pd.DataFrame(features, index=texts.index)
@classmethod
def _build_weekly_group(cls, df):
# index情報から、(year, week)の情報を得る。
return pd.Series(list(zip(df.index.year, df.index.week)), index=df.index)
@classmethod
def build_weekly_features(cls, features, boundary_week):
assert isinstance(boundary_week, tuple)
weekly_group = cls._build_weekly_group(df=features)
features = features.groupby(weekly_group).apply(lambda x: x[:])
train_features = features[features.index.get_level_values(0) <= boundary_week]
test_features = features[features.index.get_level_values(0) > boundary_week]
return {"train": train_features, "test": test_features}
@classmethod
def generate_lstm_features(
cls,
article_path,
start_dt=None,
boundary_week=(2020, 26),
target_feature_types=None,
):
# target_feature_typesが指定されなかったらデフォルト値設定
dfault_target_feature_types = [
"headline",
"keywords",
]
if target_feature_types is None:
target_feature_types = dfault_target_feature_types
# feature typeが想定通りであることを確認
assert set(target_feature_types).issubset(dfault_target_feature_types)
# ニュースデータをロードする。
articles = cls.load_articles(start_dt=start_dt, path=article_path)
# 前処理を行う。
articles = cls.normalize_articles(articles)
articles = cls.handle_punctuations_in_articles(articles)
articles = cls.drop_remove_list_words(articles)
# headlineとkeywordsの特徴量をdict型で返す。
lstm_features = {}
for feature_type in target_feature_types:
# コーパス全体のBERT特徴量を抽出する。
features = cls.generate_features_by_texts(texts=articles[feature_type])
# feature_typeに合致するfeature_combiner_handlerをclsから取得する。
feature_combiner_handler = {
"headline": cls.headline_feature_combiner_handler,
"keywords": cls.keywords_feature_combiner_handler,
}[feature_type]
# 特徴量を週毎のグループ化する。
weekly_features = cls.build_weekly_features(features, boundary_week)["test"]
# Sentiment scoreを抽出する。
lstm_features[
f"{feature_type}_features"
] = feature_combiner_handler.generate_by_weekly_features(
weekly_features=weekly_features,
generate_target="sentiment",
max_sequence_length=10000,
)
return lstm_features6.3. 合成特徴量の解析
前章においてLSTMモデルを作成し、合成特徴量であるfeaturesとsentiment scoreを抽出しました。sentiment scoreは、featuresから線形次元圧縮されたものであり、featuresと比べより低次元の情報を保持しています。しかし、使用時の容易性を考慮し、以降のチュートリアルにおいては、sentiment scoreのみを用いてマーケット予測のモデリングを行います。本節では、sentiment scoreがどのような性質を持っているかを確認するため、予測対象となるマーケットのforward returnとの関係性を解析します。
6.3.1. 合成特徴量のデータのロード
抽出したsentiment scoreを読み込みます。columnは、次元順に付与されたidを表します。sentimentの場合は1次元のみのデータとなっているため、0でインデクシングし、解析ではpd.series形式として扱います。
headline_features = pd.read_pickle(f'{CONFIG["base_path"]}/headline_features/LSTM_sentiment.pkl')[0].rename('features')
keywords_features = pd.read_pickle(f'{CONFIG["base_path"]}/keywords_features/LSTM_sentiment.pkl')[0].rename('features')
display(headline_features.head())
display(keywords_features.head())出力結果は以下の通りです。現在、LSTMの出力値は、値上がりと値下がりの確率となり、値下がり時は0、値上がり時は1に近い値を出力するように学習しています。十分なデータを揃えてモデルの学習を収束することができれば、実際に0に近い値、1に近い値なども出力するようになりますが、今回のように収束するほどのデータ量がない場合、学習時に観察したラベルの平均値や0.5近辺にモデルの出力は近くなります。マーケットデータのような一般的に学習の難しいデータでは、この現象が起きやすいことに注意してください。ただし、出力自体はきちんと入力データに対して変化していることが確認できるので、相対的な出力の強さを計測することでスコア化することもでき、相関係数や順位相関係数を用いてスコアの評価を実施することも可能です。
(2020, 27) 0.601928
(2020, 28) 0.606229
(2020, 29) 0.603833
(2020, 30) 0.601890
(2020, 31) 0.605760
Name: features, dtype: float32
(2020, 27) 0.506807
(2020, 28) 0.508067
(2020, 29) 0.506754
(2020, 30) 0.506794
(2020, 31) 0.507054
Name: features, dtype: float326.3.2. 評価用ラベルをビルド
上記で作成したマーケットのweekly_fwd_returnの作成ロジックと同様に、評価用ラベルである次週のマーケットのリターンを作成します。
# boundary_weekを学習時境界と同様に設定し、weekly_fwd_returnsをビルドする。
weekly_group = SentimentGenerator._build_weekly_group(df=stock_price)
weekly_returns = stock_price.groupby(weekly_group).apply(_compute_weekly_return)
weekly_fwd_returns = weekly_returns.shift(-1).rename('weekly_fwd_returns')
# 特徴量の期間と同様の期間のデータのみを使用する。
weekly_fwd_returns = weekly_fwd_returns.reindex(headline_features.index)
display(weekly_fwd_returns)出力結果は以下の通りです。
(2020, 27) -0.017781
(2020, 28) 0.016613
(2020, 29) 0.001590
(2020, 30) -0.048742
(2020, 31) 0.029370
(2020, 32) 0.039417
(2020, 33) 0.000009
(2020, 34) -0.006018
(2020, 35) 0.003958
(2020, 36) 0.023614
(2020, 37) 0.021705
(2020, 38) -0.000459
(2020, 39) -0.024606
(2020, 40) 0.017951
(2020, 41) -0.022318
(2020, 42) 0.000046
(2020, 43) -0.033692
(2020, 44) 0.040975
(2020, 45) 0.000463
(2020, 46) -0.004318
(2020, 47) 0.008869
(2020, 48) -0.002206
(2020, 49) -0.003282
(2020, 50) 0.001516
(2020, 51) -0.009117
(2020, 52) 0.005004
Name: weekly_fwd_returns, dtype: float646.3.3. 合成特徴量とラベル間の相関の確認
合成特徴量と上で作成したラベル間の相関を調べます。
# 二つのpd.Seriesをconcatenateする。
# indexの違いがあるため、片方だけ存在するデータはドロップする。
df = pd.concat([headline_features, weekly_fwd_returns], axis=1, sort=True).dropna()
# 二つのコラムのシークエンス間の相関は、以下のように取得できる。
display(df.corr()[df.columns[0]][df.columns[-1]])出力結果は以下の通りです。
0.6040216860152573次に、corr関数にmethodを指定して、pearsonの相関係数及びspearmanの順位相関係数を計算します。
def display_corr(df):
display(pd.Series(
{
"pearson": df.corr(method='pearson')[df.columns[0]][df.columns[-1]],
"spearman": df.corr(method='spearman')[df.columns[0]][df.columns[-1]]
}
))
display_corr(df)出力結果は以下の通りです。
pearson 0.604022
spearman 0.566496
dtype: float64上記の関数をheadline, keywords両方に適用し、ラベルとの相関を表示します。
for features, feature_type in [(headline_features, 'headline_features'), (keywords_features, 'keywords_features')]:
display_markdown(f'#### feature_type: {feature_type}', raw=True)
df = pd.concat([features, weekly_fwd_returns], axis=1, sort=True).dropna()
display_corr(df)出力結果は以下の通りです。headline_featuresはpearson相関係数が0.60、spearmanの相関係数が0.57となっています。keywords_featuresは若干相関係数が下がりますが、それでも十分に高い相関係数を保持しています。
参考までに相関係数0.6というのは株式予測における予測スコアと未来の変化率の相関係数としては高い数値です。通常、株式の予測モデル(高値・安値の予測モデルではないことに注意してください)と未来の変化率の相関係数(情報係数ともよばれます)は、10年程度の十分に長い期間で検定した時は0.1から0.2に到達すれば優秀なモデルといわれています(シストレのススメ 3.5.投資指標の探索要領より引用 http://we.love-profit.com/entry/2018/04/01/152750 )。
0.6という今回の結果は、2020年後半という非常に限定された期間のバックテスト結果ですので、この手法によるスコアが未来まで高いパフォーマンスを発揮するかは現時点で判断できません。これは学習に利用した2020年前半のデータ・ラベルの分布と評価に利用した期間のデータ・ラベルの分布が似通っていることが原因だろうと推測されます。5章でコーパスを確認したときも、「コロナウィルス」などが頻出単語として登場しましたが、2020年のように年間を通して一つの「コロナウィルス」という単語がニュースデータで支配的であることは稀であり、この非常に高いパフォーマンスは2020年のデータ・ラベルの分布が原因であろうと考察されます。
feature_type: headline_features
pearson 0.604022
spearman 0.566496
dtype: float64
feature_type: keywords_features
pearson 0.565515
spearman 0.474872
dtype: float646.4. 結果の可視化
結果の妥当性を検証するため、さらに詳しい可視化を実施していきます。結果の可視化は主に以下の観点のために必要です。
-
時系列的に予測の方向性などが集中していないか
-
上げ・下げのどちらかにスコアが偏っていないか
-
どの時期に精度が高く、どの時期に精度が低いか
実際に相関係数や精度は単一の評価軸であり、可視化を通して、その結果が本当に妥当性が高いかを検証するのは非常に重要な作業です。
6.4.1. 回帰分析による可視化
回帰分析による可視化を行います。
# 回帰を行うため、xとyとなるコラムを設定する。
x_column = 'features'
y_column = 'weekly_fwd_returns'
# stats.linregressを用いて、単回帰直線の係数とバイアスを取得する。
df = pd.concat([headline_features, weekly_fwd_returns], axis=1, sort=True).dropna()
coef, bias, _, _, _ = stats.linregress(x=df[x_column], y=df[y_column])
print(f'coef: {coef:.4f}, bias: {bias:.4f}')出力結果は以下の通りです。
coef: 6.6302, bias: -4.0035これらの情報をseabornのregression plotと共に表示します。
def display_regplot(df, x_column='features', y_column='weekly_fwd_returns'):
# stats.linregressを用いて、単回帰直線の係数とバイアスを取得する。
coef, bias, _, _, _ = stats.linregress(x=df[x_column], y=df[y_column])
# seabornのregplotを用いて、単回帰直線及び、scatter sampleを表示する。
_, ax = plt.subplots(1, 1, figsize=(6, 4))
sns.regplot(
x=x_column,
y=y_column,
data=df,
ax=ax,
line_kws={
"label": "y={0:.4f}x+{1:.4f}".format(coef, bias), # 取得した係数とバイアスを用いて単項式を表示する。
},
)
plt.legend()
plt.show()
for features, feature_type in [(headline_features, 'headline_features'), (keywords_features, 'keywords_features')]:
display_markdown(f'#### feature_type: {feature_type}', raw=True)
df = pd.concat([features, weekly_fwd_returns], axis=1, sort=True).dropna()
display_regplot(df=df)出力結果は以下の通りです。headline_featuresは、x軸のfeaturesがkeywords_featuresより若干ですが幅広に分布しており、keywords_featuresよりも上手く学習が出来た可能性を示しています。また。スコアが低い時にy軸の次の週の投資対象のユニバースの平均変化率が低く、スコアが高い時に平均変化率が高い傾向がはっきりと確認できます。また、スコアが中間の場合は平均変化率も0近辺に集中しており、全体的に信頼性の高い結果となっていることがわかります。keywords_featuresの結果も良いものですが、headline_featuresほどは優れていません。お互いの相関が低ければ、アンサンブルを考慮する価値はありそうですので、時系列の可視化を実施してみます。
6.4.2. 時系列的な関係の可視化
barplotにより、特徴量とラベル間での時系列的な関係を確認します。
df.plot(kind='bar', figsize=(16, 3))出力結果は以下の通りです。
二つのデータを一つの軸上で単純にプロットすると値のノルム、平均、分散の違いから、相互的な動きを確認しにくいです。ここでは、手元にあるデータを平均と分散を用いてノーマライズしたzscore標準化( https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.zscore.html )を使って相互の関係を可視化してみましょう。
def normalize(df):
# zscore normalizeする。
return pd.DataFrame(stats.zscore(df), index=df.index, columns=[f'Z({column})' for column in df.columns])
def display_bar_plot(df):
# zscore normalizeしたデータを用いてbarplotする。
normalize(df).plot(kind='bar', figsize=(16, 3))
plt.show()
for features, feature_type in [(headline_features, 'headline_features'), (keywords_features, 'keywords_features')]:
display_markdown(f'#### feature_type: {feature_type}', raw=True)
df = pd.concat([features, weekly_fwd_returns], axis=1, sort=True).dropna()
display_bar_plot(df=df)出力結果は以下の通りです。headline_featuresは時系列的に上下の予測が固まっておらず、安定的に分布しており次の週のマーケットのセンチメントを的確に捉えている可能性が高そうです。headline_featuresとkeywords_featuresの予測スコアは時系列的に似通っているため、無理にアンサンブルなどは実施せず、以降はシンプルにheadline_featuresを活用するものとします。
6.5. ストラテジーへの適用の実装例
ここでは、予測スコアを利用して現金比率を操作するサンプルコードを示します。本章はLSTMにより目的関数を設定したスコアをニュースデータから取得することが目的であり、バックテストコードを紹介することが目的ではないため、ここではサンプル実装を示す程度にとどめます。以下の実装例では、データを扱いやすくするためにzscore標準化を実施し、その分布に応じて現金比率を操作するロジックを実装しています。
def get_cash_ratio(cls, df_sentiment):
"""
headline_m2_sentimentの値が低い時はリスクとみなし
現金保有量を多くする。
入力:
センチメント (DataFrame): センチメント情報
出力:
現金比率 (Dataframe): 入力値に現金比率を追加したもの
"""
# リスク値マッピング用の分布取得期間
DIST_START_DT = "2020-06-29"
DIST_END_DT = "2020-09-25"
# リスク値を計算する期間
USE_START_DT = "2020-10-02"
# 出力用にコピー
df_sentiment = df_sentiment.copy()
# headline_m2_sentiment_0の値が高いほどポジティブなので符号反転させる
sentiment_dist = sorted(df_sentiment.loc[DIST_START_DT:DIST_END_DT, "headline_m2_sentiment_0"].values * -1)
sentiment_use = df_sentiment.loc[USE_START_DT:, "headline_m2_sentiment_0"].values * -1
display(sentiment_dist)
display(sentiment_use)
# DIST_START_DT:DIST_END_DTの分布を使用してリスク判定する
z = zscore(sentiment_dist)
# 閾値を決定
p = np.percentile(z, [25, 50, 75])
# リスク値を計算する
u = zscore(sentiment_use)
# 分布から現金比率の割合を決定
d = np.digitize(u, p)
# 出力用に整形して 0, 10, 20, 30 のいずれか返すようにする
df_sentiment.loc[USE_START_DT:, "risk"] = d * 10
return df_sentiment現金比率の操作以外の活用方法としては、LSTMのような学習レイヤーが存在すると、ユニバースの時価総額やROEが高い銘柄と低い銘柄のどちらがより多くのリターンを産み出すかを予測させるようなストラテジーを構築することもできます。是非自由な発想でBERT特徴量を活用してみてください。
6.6. 投稿用コードの実装例
5章からここまでで、ニュースデータから現金比率を操作するまでのコードを提示してきました。これまで提示したコードを組み合わせて実装することで、ランタイム環境で動作する投稿用のモデルを作ることができますが、具体的な実装方法に悩まれるかもしれません。本チュートリアルでは実際に投稿してリーダーボードで動作を確認可能な実装例を handson/Chapter06/archive/src 配下に配置しています。本チュートリアル内では実装例の詳細な解説はいたしませんが、実装例のコードをご覧いただくことで独自実装や改良等のヒントとなるかもしれません。
以下では、実装例のコードを実際に動作させるために必要なファイルの配置や投稿のためのパッケージ作成を解説いたします。本作業内容は handson/Chapter06/20210224_chapter06_tutorial_test_predictor.ipynb として nootbook にも記載していますので、実際の動作確認などはそちらをご使用ください。なお、実装例の確認については Google Colab 環境で実施します。
実装例の配置場所
handson/Chapter06/
|-- 20210224_chapter06_tutorial_test_predictor.ipynb <= 実装例の動作確認用ノートブック
|-- 20210226_chapter06_tutorial.ipynb <= 本章の作業用ノートブック
`-- archive
|-- model
| `-- 本ディレクトリ内に事前学習済みのモデルやパラメーターを配置します。
|-- requirements.txt <= 実装例を動作させるために必要なモジュールを記載しています。
`-- src
|-- module.py <= 5章/6章のコードをまとめたもの
`-- predictor.py <= 4章で作成したScoringServiceクラスに現金比率操作用コード追加した実装例6.6.1. 事前準備
本ノートブックは Google Colaboratory で実行することを想定しています。実行時には以下の事前準備が必要です。
-
コンペティションページから必要なファイルのダウンロード
-
Google Drive に必要ファイルを配置
6.6.2. コンペティションページから必要なファイルのダウンロード
■以下の10個のファイルを本コンペティションのデータタブから取得します。 https://signate.jp/competitions/443/data
2章で作成した学習済みモデル
-
01 my_model_label_high_20.pkl
-
02 my_model_label_low_20.pkl
LSTMモデルの学習済みパラメータ (headline_features)
-
03 19.ckpt
LSTMモデルの出力 (headline_features)
-
04 LSTM_sentiment.pkl
動作確認用データ
-
05 nikkei_article.csv.gz
-
06 stock_fin.csv.gz
-
07 stock_fin_price.csv.gz
-
08 stock_list.csv.gz
-
09 stock_price.csv.gz
-
10 tdnet.csv.gz
■以下の4つのファイルをチュートリアルのリポジトリから取得します。 https://github.com/JapanExchangeGroup/J-Quants-Tutorial/tree/main/handson/Chapter06
動作確認用ノートブック (本ノートブック)
-
11 20210224_chapter06_tutorial_test_predictor.ipynb
実装例のrequirements.txt
-
12 archive/requirements.txt
実装例のコード
-
13 archive/src/module.py
-
14 archive/src/predictor.py
6.6.3. Google Drive に必要なファイルを配置
Google Drive の My Drive 配下に以下のフォルダ構造でファイルを配置します。ファイル名の後ろに「download:数字」として、先程のダウンロード時の説明で使用した番号を記載しています。
MyDrive/JPX_competition/
├── Chapter06
│ ├── 20210224_chapter06_tutorial_test_predictor.ipynb <= 本ノートブック download:11
│ └── archive <= 投稿用パッケージの起点となるフォルダ
│ ├── model
│ │ ├── headline_features
│ │ │ ├── 19.ckpt <= 6章で作成した LSTM モデルの学習済みパラメータ download:03
│ │ │ └── LSTM_sentiment.pkl <= 6章で作成したセンチメント download:04
│ │ ├── my_model_label_high_20.pkl <= 2章で作成した最高値予測モデル download:01
│ │ ├── my_model_label_low_20.pkl <= 2章で作成した最安値予測モデル download:02
│ ├── src
│ │ ├── module.py <= 5章/6章のコードをまとめたもの download:13
│ │ └── predictor.py <= 4章のコードに一部追記してニュースデータを使用して現金比率操作を追記したもの download:14
│ └── requirements.txt
└── data_dir_comp2
├── nikkei_article.csv.gz <= download:05
├── stock_fin.csv.gz <= download:06
├── stock_fin_price.csv.gz <= download:07
├── stock_list.csv.gz <= download:08
├── stock_price.csv.gz <= download:09
└── tdnet.csv.gz <= download:106.6.4. 実行環境設定
本ノートブックを実行するにあたって必要な環境設定を実施します。
-
Google Driveのマウント
-
モジュールをimportするためにsys.pathを追加
-
autoreload 拡張有効化
-
必要なライブラリのインストール
-
使用するディレクトリの設定
-
入力パラメータ作成
-
BERTの事前学習済みモデルをダウンロード
Google Driveのマウント
Google Driveをマウントします。
import sys
if 'google.colab' in sys.modules:
# Google Drive をマウントします
from google.colab import drive
mount_dir = "/content/drive"
drive.mount(mount_dir)使用するディレクトリの設定
環境に応じて使用するディレクトリを設定します。配置した.pyファイルをimportできるようにsys.pathに配置先のディレクトリを追加しています。
if 'google.colab' in sys.modules:
# Google Colab環境では上記に示したディレクトリ設定を使用します。
# archiveディレクトリを指定します。
archive_path = f"{mount_dir}/MyDrive/JPX_competition/Chapter06/archive"
# 実装例のコードを配置したディレクトリを指定します。
src_path = f"{mount_dir}/MyDrive/JPX_competition/Chapter06/archive/src"
# sys.pathを設定
sys.path.append(src_path)
# ダウンロードしてきたデータを配置したディレクトリを設定します。
dataset_dir = f"{mount_dir}/MyDrive/JPX_competition/data_dir_comp2"
# 2章のモデルを配置したディレクトリを設定します。
# このディレクトリにBERTの事前学習済みモデルをダウンロードして保存します。
model_path = f"{mount_dir}/MyDrive/JPX_competition/Chapter06/archive/model"
# テスト用に出力したポートフォリオを保存するディレクトリを設定します
output_path = f"{mount_dir}/MyDrive/JPX_competition/Chapter06"
else:
# archiveディレクトリを指定します。
archive_path = "archive"
# 実装例のコードを配置したディレクトリを指定します。
src_path = "archive/src"
# sys.pathを設定
sys.path.append(src_path)
# ダウンロードしてきたデータを配置したディレクトリを設定します。
dataset_dir = "/notebook/data_dir_comp2"
# 2章のモデルを配置したディレクトリを設定します。
# このディレクトリにBERTの事前学習済みモデルをダウンロードして保存します。
model_path = "archive/model"
# テスト用に出力したポートフォリオを保存するディレクトリを設定します
output_path = "."必要なライブラリのインストール
必要なライブラリをインストールします。
# neologdnのためにg++をインストール
! apt-get update
! apt-get install -y --no-install-recommends g++# 必要なライブラリをインストール
!pip install -r $archive_path/requirements.txt入力パラメータ作成
ランタイム環境でpredictメソッドが呼ばれるときに渡される inputs パラメーターを実行環境に合わせて作成します。
# predictメソッドへの入力パラメーターを設定します。
# ランタイム環境での実行時と同一フォーマットにします
inputs = {
"stock_list": f"{dataset_dir}/stock_list.csv.gz",
"stock_price": f"{dataset_dir}/stock_price.csv.gz",
"stock_fin": f"{dataset_dir}/stock_fin.csv.gz",
"stock_fin_price": f"{dataset_dir}/stock_fin_price.csv.gz",
# ニュースデータ
"tdnet": f"{dataset_dir}/tdnet.csv.gz",
"disclosureItems": f"{dataset_dir}/disclosureItems.csv.gz",
"nikkei_article": f"{dataset_dir}/nikkei_article.csv.gz",
"article": f"{dataset_dir}/article.csv.gz",
"industry": f"{dataset_dir}/industry.csv.gz",
"industry2": f"{dataset_dir}/industry2.csv.gz",
"region": f"{dataset_dir}/region.csv.gz",
"theme": f"{dataset_dir}/theme.csv.gz",
# 目的変数データ
"stock_labels": f"{dataset_dir}/stock_labels.csv.gz",
# 購入日指定データ
"purchase_date": f"{dataset_dir}/purchase_date.csv"
}6.6.5. BERTの事前学習済みモデルをダウンロード
ランタイム環境ではインターネットにアクセスできないため、BERTの事前学習済みモデルを {model_path}/transformers 配下にダウンロードしておきます。
SentimentGeneratorのload_feature_extractorおよびload_bert_tokenizerメソッドにdownloadおよびsave_localパラメータをTrueとして実行することで、BERTの事前学習済みモデルをダウンロードおよび保存します。次にSentimentGenratorを読み込みます。
from module import SentimentGenerator事前学習済みのBERTモデルをダウンロードして保存します。
SentimentGenerator.load_feature_extractor(model_path, download=True, save_local=True)事前学習時に使用したTokenizerも合わせてダウンロードして保存します。
SentimentGenerator.load_bert_tokenizer(model_path, download=True, save_local=True)BERTの事前学習済みモデルが保存されていることを確認します。
! ls -lhR $model_path出力
/content/drive/MyDrive/JPX_competition/comp2/chapter06/archive/model:
total 71M
drwx------ 2 root root 4.0K Mar 11 07:37 headline_features
-rw------- 1 root root 36M Mar 11 07:37 my_model_label_high_20.pkl
-rw------- 1 root root 36M Mar 11 07:37 my_model_label_low_20.pkl
drwx------ 3 root root 4.0K Mar 11 07:37 transformers_pretrained
/content/drive/MyDrive/JPX_competition/comp2/chapter06/archive/model/headline_features:
total 5.1M
-rw------- 1 root root 5.1M Mar 11 07:37 19.ckpt
-rw------- 1 root root 958 Mar 11 07:37 LSTM_sentiment.pkl
/content/drive/MyDrive/JPX_competition/comp2/chapter06/archive/model/transformers_pretrained:
total 4.0K
drwx------ 3 root root 4.0K Mar 11 07:37 cl-tohoku
/content/drive/MyDrive/JPX_competition/comp2/chapter06/archive/model/transformers_pretrained/cl-tohoku:
total 4.0K
drwx------ 2 root root 4.0K Mar 11 07:37 bert-base-japanese-whole-word-masking
/content/drive/MyDrive/JPX_competition/comp2/chapter06/archive/model/transformers_pretrained/cl-tohoku/bert-base-japanese-whole-word-masking:
total 423M
-rw------- 1 root root 707 Mar 11 07:37 config.json
-rw------- 1 root root 423M Mar 11 07:37 pytorch_model.bin
-rw------- 1 root root 112 Mar 11 07:37 special_tokens_map.json
-rw------- 1 root root 397 Mar 11 07:37 tokenizer_config.json
-rw------- 1 root root 252K Mar 11 07:37 vocab.txt6.6.6. ランタイム環境を想定したテスト実行
ランタイム環境で実行されるのと同等の呼び出し方でテストを行います。まずは、ScoringServiceクラスを読み込みます。
from predictor import ScoringServiceget_modelメソッドを呼び出すことで以下を実施します。
-
BERTの事前学習済みモデルを読み込み
-
BERTの事前学習済みモデルに使用したTokenizerを読み込み
-
事前学習済みの最高値・最安値モデルを読み込み
ScoringService.get_model(model_path)今回はランタイム環境と同一のデータセットを使用していないため、ダウンロードしたデータを使用して動作確認するために予測出力対象日 (start_dt) を 2020-12-28 と指定したpurchase_dateファイルを作成します。このコードを実行することで既に purchase_date.csv が存在している場合は上書きされることに注意してください。
! echo "Purchase Date" > $dataset_dir/purchase_date.csv
! echo "2020-12-28" >> $dataset_dir/purchase_date.csv予測を実行します。
ret = ScoringService.predict(inputs)6.6.7. 出力の確認
予測出力の実行結果を確認します。確認ポイントは以下になります。
-
出力のフォーマットが規定されているものと一致していること
print("\n".join(ret.split("\n")[:10]))出力
date,Local Code,budget
2020-12-28,4165,20000
2020-12-28,7694,20000
2020-12-28,4167,20000
2020-12-28,3677,20000
2020-12-28,4493,20000
2020-12-28,7358,20000
2020-12-28,8848,20000
2020-12-28,3328,20000
2020-12-28,6050,20000# 出力を保存
with open(f"{output_path}/chapter06-tutorial-1.csv", mode="w") as f:
f.write(ret)6.6.8. 投稿用パッケージを作成
上記で動作確認したモデルを投稿用にパッケージ化します。
import os
import zipfile
# 提出用パッケージ名
package_file = "chapter06-model.zip"
# パッケージファイルパス
package_path = f"{output_path}/{package_file}"
# zipファイルを作成
with zipfile.ZipFile(package_path, "w") as f:
# requirements.txt を追加
print(f"[+] add {archive_path}/requirements.txt to requirements.txt")
f.write(f"{archive_path}/requirements.txt", "requirements.txt")
# model/配下を追加
for root, dirs, files in os.walk(model_path):
for file in files:
add_path = os.path.join(root, file)
rel_path = os.path.relpath(
os.path.join(root, file),
os.path.join(model_path, '..')
)
print(f"[+] add {add_path} to {rel_path}")
f.write(add_path, rel_path)
# src/module.py を追加
print(f"[+] add {src_path}/module.py to src/module.py")
f.write(f"{src_path}/module.py", "src/module.py")
# src/predictor.py を追加
print(f"[+] add {src_path}/predictor.py to src/predictor.py")
f.write(f"{src_path}/predictor.py", "src/predictor.py")
print(f"[+] please check {package_path}") 上記コードを最後まで実行するとGoogle Drive に投稿用の chapter06-model.zip ファイルが作成されているため、そちらをダウンロードして投稿しましょう。
7. tips集
本章では、本コンペティションに関連する金融・データ解析一般についてのtipsを紹介します。
7.1. コンペティションフォーラムの紹介
J-Quantsでは、コンペティションに関連して執筆された記事の投稿やチュートリアルへのご質問をフォーラム( "https://signate.jp/competitions/423/discussions" )にて募集しております(コンペの登録が必要)。また、下記内容以外にも有志の方による素晴らしいスレッドがありますので、ぜひご確認ください。
| タイトル | URL |
|---|---|
参考書籍・記事・知見共有スレッド |
|
Web記事投稿スレッド |
|
チュートリアル質問用スレッド |
7.2. 金融用語集
本コンペティションで必要となる専門用語を解説してくれているサイトをご紹介します。
もし、専門用語で困った場合は、下記リンク先のコンテンツを確認していただければ幸いです。
| タイトル | 運営元 | URL |
|---|---|---|
証券用語解説集 |
野村證券 |
|
金融・証券用語解説集 |
大和証券 |
|
ファイナンス用語集 |
みずほ証券 |
|
初めてでもわかりやすい用語集 |
SMBC日興証券 |
|
用語解説 |
三菱UFJモルガン・スタンレー証券株式会社 |
|
金融用語解説(知るぽると) |
金融広報中央委員会 |
|
金融・証券用語集 |
日本証券業協会 |
|
用語集 |
EY新日本有限責任監査法人 |
|
会計監査用語解説集 |
日本公認会計士協会 |
|
財務諸表等の用語、様式及び作成方法に関する規則 |
e-GOV |
|
用語集 |
野村アセットマネジメント |
|
用語集 |
アセットマネジメントOne |
|
用語集 |
大和アセットマネジメント |
|
わかりやすい用語集 |
三井住友DSアセットマネジメント |
7.3. 東証マネ部
「東証 マネ部!」は身近なお金の話から、プロが教える資産運用のノウハウまで 、資産形成についてわかりやすく解説するサイトです。 今回は、コンペに関係がありそうな記事をピックアップしてみました。コンペティションの息抜きにぜひご確認ください。
| タイトル | リンク |
|---|---|
投資に不可欠な財務三表の見方 |
|
財務ニュースを読む |
|
長期投資に欠かせない運用コストを意識しよう |
|
プロの投資家が注目する指標「ROE」とは? |
|
ディープラーニングが拓く「AI投資」の可能性 |
|
AIが導く金融市場の未来 |
|
4大投資指標のワナ~解析力の鍛錬~ |
|
AIを使った市場の予測に挑む「AlpacaJapan」 |
|
「AIと資産運用」 |
|
投資に役立つ「会社四季報」活用のポイント |
|
最低投資金額50万円以下の銘柄特集 |
|
クチコミで投資を楽しめるアプリ「ferci(フェルシー)」 |
|
コロナ後の世界 |
|
株式場況を読む~専門用語の理解~ |
|
決算ニュースを読む~会計用語の理解~ |
|
公的統計を補完する「オルタナティブデータ」とは? |
7.4. 参考になる書籍
本コンペティションに参考になる書籍を紹介致します。
| タイトル | 著者 | 概要 |
|---|---|---|
ファイナンス機械学習―金融市場分析を変える機械学習アルゴリズムの理論と実践 |
マルコス・ロペス・デ・プラド |
機械学習を用いて金融データを分析する上での知識を網羅的に学ぶことができる。金融のドメイン知識をデータサイエンティストが学ぶには最適な本。 |
アセットマネージャーのためのファイナンス機械学習 |
マルコス・ロペス・デ・プラド |
ファイナンス機械学習に続き、ノイズ除去、クラスタリング、ラベリング、特徴量の重要度分析などの本コンペでも関連の深いトピックを学ぶことができる。ただし、「ファイナンス機械学習」と比較すると網羅性はないので、2冊目として読むことを推奨。 |
Kaggleで勝つデータ分析の技術 |
門脇 大輔 他 |
モデルのチューニング・アンサンブルなど機械学習のコンペに関連するテクニックを効率的に学ぶことができる。 |
株を買うなら最低限知っておきたい ファンダメンタル投資の教科書 改訂版 |
足立 武志 |
ファンダメンタル分析に必要な基礎知識を学ぶことができる。 |
経済・ファイナンスデータの計量時系列分析 |
沖本竜義 |
ARIMAモデルをベースとした古典的な時系列解析を学ぶことができる。ARIMAモデル自体を予測モデルとして使うことは、コンペではまれだが、金融データに対して時系列分析を実施する上での実務上の課題なども学ぶことができる。 |
金融・経済分析のためのテキストマイニング |
和泉 潔他 |
市場レポートや経済ニュースなどのテキストデータを分析し、資産運用や市場分析に活かす手法を解説している。数式は少なく、金融テキストマイニングの独特な注意点や思考法を中心に整理しており、初めて金融分野のテキストマイニングをする人には助かる一冊。 |
統計学入門 |
東京大学教養学部統計学教室 編 |
文科と理科両方の学生のために,統計的なものの考え方の基礎がやさしく解説されており、統計学の体系的な知識を与えるように,編集・執筆された一冊。 |
Pythonデータサイエンスハンドブック |
Jake VanderPlas 著、菊池 彰 訳 |
本チュートリアルにおいても利用されているJupyter、NumPy、pandas、Matplotlib、scikit-learn等をカバーしている一冊。それぞれのトピックについて、押さえておくべき基本、tips、便利なコマンドなどが紹介されている。 |
7.5. 参考になるコンペティション
本コンペティションに関連したコンペティションを紹介いたします。
| タイトル | 概要 | URL |
|---|---|---|
Two Sigma: Using News to Predict Stock Movements |
ニュースデータを用いた株価の予測 |
|
Fintech Data Championship |
日本株式のポートフォリオで次の1カ月後に、最も上昇する組み合わせを検討 |
|
Algorithmic Trading Challenge |
投資戦略に関する収益率・取引高等のデータから、各戦略への資金の割り当ての重みを最適化 |
|
大手ヘッジファンドX: 金融モデリングチャレンジ |
独自に導出した様々な特徴量から将来の動きを予想 |
|
財務・非財務情報を活用した株主価値予測 |
会計年度2014-2017年の各企業の財務・非財務情報から、会計年度2018年の期末時価総額を予測 |
|
The Winton Stock Market Challenge |
過去の株価とマスクされた特徴量から将来の株価を予想 |
|
Numerai |
マスクされた銘柄・特徴量から週次で予測結果を提出 |
|
Quantconnect |
条件を満たしたモデルでリターンを追求 |
|
Bloomberg |
ESG要素を効果的に投資判断に組み込んでいるかなどの評価 |
https://www.bloomberg.co.jp/company/stories/investment_contest_2020/ |
Jane Street Market Prediction |
株の取引戦略を採用するかどうかを予測 |
7.6. ファンダメンタルズ分析の活用方法
ファンダメンタルズ分析とは、企業の成長性、収益性、割安性、安定性、効率性などを分析し、投資判断などに活用する手法です。ここでは成長性、収益性、割安性、安定性、効率性の代表的な指標を紹介します。
(成長性)
成長性とは、売上や利益の増加が継続しているかを指し、企業価値の増大に直結する指標です。本コンペのデータでは、純資産や営業利益の上昇率に着目することで、その銘柄の成長性を測ることが出来ます。営業利益の上昇率を計算する場合は、季節性を考慮し、前年同期比と比較することが多いです。
また、年間を通して同一の指標で評価を行いたいときは、直近の四半期のデータで移動平均などを取る方法があります。成長性について利用される様々な指標として売上高増加率、営業利益増加率、経常利益増加率、総資本増加率、純資本増加率、従業員増加率、一株当たり当期純利益(EPS)(成長性分析で企業の成長度を測る 知っておくべき指標や分析方法 より引用 https://keiei.freee.co.jp/articles/c0201686 )などがあります。
なお、過去の成長性を解析することはできますが、その成長性が長期間に渡って継続するかを予測することは、様々な要因が関係するため難しい問題です。また、株価そのものではなく成長性自体をモデルの予測対象にして、その予測に基づき投資を行うスタイルも存在します。
(収益性)
収益性は、営業利益率や経常利益率等を指し、それぞれ営業利益、経常利益を売上高で割ることで計算されます。営業利益率や経常利益率が高い企業は優れたビジネスモデルを保持していたり、販管費を低く保つオペレーションが徹底されていたりすることが多く、優良企業を判断する上での指標となっています。そして、この収益性の変化率を成長性と扱うこともできます。
一般的に投資家が期待する収益性は、業種において大きく異なることに注意が必要です。
例えば、様々ある業種のうち、情報通信と食品に期待される営業利益率は大きく異なることが想定されます。この場合、銘柄情報にはセクター情報が含まれているため、セクター平均の営業利益率を計算し、その差分を計算することで、セクター平均からの上振れや下振れを特徴量にすることができます。
(割安性)
株式が割安であるとは、その企業の株価が企業価値と比較して安いということです。代表的な指標としてはPBRが挙げられます。この指標は、企業の純資産と発行済み株式数を割って、1株当たりの純資産を計算します。そして、現在の株価をこの1株当たりの純資産で割ってPBRを求めます。この指標が1を割っている場合は、その企業の本来の価値よりも安い値段で株を買えることになるので、割安であると考えることができます。PBRが高い銘柄をグロース銘柄、低い銘柄をバリュー銘柄として扱いそれぞれ異なる特性を持った銘柄として分析することもあり、企業の状態を知る上で重要な指標です。
現状の日本マーケットにおいては、PBRが1未満の銘柄が数多くあります(Yahooファイナンス 低PBRランキングより引用 https://info.finance.yahoo.co.jp/ranking/?kd=12 )。 これらの極めて割安な銘柄はディープバリュー株と呼ばれています。PBRが低い理由として以下のような理由も考えられますので、PBRをもって一概に割安銘柄とするのではなく、各企業のその他の決算情報を参照するなど、複数の情報を考慮することも重要です。
-
株式市場全体が調整局面にあるなどの理由により、企業実態より株価が売り込まれている。
-
含み損の実現や業績の悪化による純資産の減少を株価が先取りして織り込んで下落している。
-
不人気のため安値に放置されている。
(安定性)
安定性は、大型株や安定性が重視される金融・銀行のような特定のセクターで重視される指標です。安定性を計算する代表的な指標は「自己資本比率」です。
「自己資本比率」は総資本における自己資本の割合を計算して得られます。自己資本比率が高ければ、自己資本が多い、つまり返済義務のないお金を潤沢に持っているということになるので「中長期的に見て倒産しにくい会社」ということができ、株式の中長期保有を行う上で倒産リスクを減らすための重要なチェックポイントとなっています。(自己資本比率|会社経営の「安全性」をあらわす指標 より引用 https://advisors-freee.jp/article/category/cat-big-03/cat-small-08/9011/ )
なお、以下の効率性に関する記載でも紹介しているROEでは、当期純利益と自己資本の割合を見ますが、自己資本が低い株はROEが高くなるので注意が必要です。つまり、借り入れを増やしリスクを取っている銘柄ではROEが高くなりやすく、安定性が低くなる可能性があります。また、小型株においては安定性よりも成長性を重視することもあるという点に注意が必要です。特定のセクターや特定の領域において重要視される指標をモデルに投入する場合、セクターの情報を特徴量として投入するなど、一緒に銘柄を分類できる情報をモデルに投入することで、それらの特性を学ばせることが可能です。
(効率性)
効率性は、近年注目されているROEやROAから計算される指標です。
ROEは、当期純利益 ÷ 自己資本 × 100として計算され、自己資本に対してどれだけの利益が生み出されたのかを示します。
ROAは、借り入れなどを含む総資産を使ってどれだけ利益を生み出したかを表す指標です。
ROEやROAは、効率性を示す指標として注目されており、政府が2017年に公表した成長戦略「未来投資戦略2017」において、「《KPI》大企業(TOPIX500)の ROA について、2025 年までに欧米企業に遜色のない水準を目指す。」(未来投資戦略2017 より引用 https://www.kantei.go.jp/jp/singi/keizaisaisei/pdf/miraitousi2017_sisaku.pdf )というKPIが設定され注目を浴びています。
ROEが高い銘柄ほど効率性が高いと考えることができ、企業価値を高めるための施策としてROEの向上、または維持を目標とする企業が多く、ROE重視の流れの背景は「投資指標としての ROE」(https://www.tr.mufg.jp/houjin/jutaku/pdf/u201503_1.pdf) で詳しく解説されています。
上記のファンダメンタル情報は、本コンペティションで提供されるデータで計算可能ですので、様々なファンダメンタル情報を勉強することは、特徴量設計の次の一歩に繋がるでしょう。
7.7. テクニカル分析の活用方法
テクニカル分析は、将来の株価の変化を過去に発生した価格や出来高等の時系列パターンから予想・分析しようとする手法であり、メジャーな分析手法の一つです。テクニカル分析にはトレンド分析、オシレーター分析、フォーメーション分析、ローソク足分析(テクニカル指標一覧より引用 https://info.monex.co.jp/technical-analysis/indicators/ )があり、2章においてもオシレーターの代表的な分析手法の一つである「移動平均乖離率」を特徴量の一つとして採用しています。
ここでは、テクニカル分析を更に活用するための注意事項を説明します。テクニカル分析を特徴量として採用する場合、テクニカル分析により得た新規の情報がすでに投入済みの特徴量と比較して、どの程度新しい情報を保持しているか、という観点から考えることが重要です。
例えば、移動平均と移動平均乖離率は、それぞれ似たような情報を保持していることが容易に想像がつきます。これらの情報を特徴量として考えた場合、「20日移動平均乖離率」の方が0平均となるため、定常性を仮定することができ、扱いやすいことから移動平均乖離率を2章では採用しています。
ストキャスティクス(詳細は https://info.monex.co.jp/technical-analysis/indicators/006.html を参照)やRSI(詳細は https://info.monex.co.jp/technical-analysis/indicators/005.html を参照)のようなオシレーター系の分析も、似通った情報を保持していることが推測できます。
機械学習のモデル構築において、若干のパラメータを変更したテクニカル分析を複数個特徴量として投入することは、ほとんどの場合良い結果に結びつきません。これは、パラメータ違いのテクニカル分析や同一種類のテクニカル分析は、ほぼ同一の情報を保持していることが多く、複数個特徴量を投入したとしても、パフォーマンスが向上する程の新規の情報を発見することが難しいためです。また、時系列解析はサンプル数が限られていることが多く、特徴量の種類を多くすると学習に必要な十分なデータ量を確保できないため、むやみに特徴量を増やすべきではなく、特徴量自体にパフォーマンス向上に結びつく新しい情報が含まれていることを重視しましょう。
例えば、2章にあるような移動平均乖離率と標準偏差の組み合わせは、お互いに直近時系列に対してトレンドとボラティリティという異なる情報を保持しているため、パフォーマンス向上に期待が持てます。テクニカル分析は順張り系、逆張り系のような系統でくくることができる(第1回 数多くあるテクニカル指標を体系的に解説より引用 https://kabu.com/investment/guide/technical/01.html )ので、それらの系統の中から選択したり、異なる系統として時間時系列に対して依存しない手法、例えば、過去の高値圏にどれだけ近づいているかを計算するような方法なども考えられます。
7.8. ファクター分析の活用方法
ファクター分析とは、投資が産み出すリターンを説明するファクターを定義し、そのファクターの挙動から分析を行う手法です。
例えば、ファーマ-フレンチの3ファクターモデルでは、株式投資が産み出すリターンをリスクプレミアム、時価総額リスクファクター、簿価時価比率リスクファクターの3要素に分解してます。(Wikipedia ファーマ-フレンチの3ファクターモデルより引用 https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A1%E3%83%BC%E3%83%9E-%E3%83%95%E3%83%AC%E3%83%B3%E3%83%81%E3%81%AE3%E3%83%95%E3%82%A1%E3%82%AF%E3%82%BF%E3%83%BC%E3%83%A2%E3%83%87%E3%83%AB )
株式投資におけるファクター分析を知っておくことは、どのような特徴量を設計するかという考察を行うために役立ちます。
例えば、主要なファクターである時価総額について考えてみましょう。本コンペで利用できるデータを利用し、株価と発行済株式数から各銘柄の時価総額を計算することができます。一般的にマーケットは小型株が優位なときもあれば、大型株が優位なときもあるため、どちらに投資するべきかを簡単に決めることはできません。しかし、この時価総額が株価のリターンの説明要因の一つであるということを知っていれば、少なくとも特徴量に追加することで何らかの学習を行える可能性があるのではと考える事ができます。時価総額が入力データに含まれていない場合、モデルは時価総額ファクターに関連した相場変動を理解することが難しくなりますので、特徴量として投入したほうが良さそうだということが推測されます。
また、近年新たな投資手法として現れたスマートベータ投資も、このファクター分析を利用したアプローチの一つであり、ファクター分析は新しい投資手法を考える上で、基礎知識の一つになっています。スマートベータ投資とは、特定のファクターをベンチマークとして制御する手法です。具体的には、高配当、バリュー、低リスク、最小分散、クオリティ、モメンタム、及びこれらの組み合わせ等が、ベンチマークとして制御するファクターの候補となっています(スマートベータとリターン特性についてより引用 https://www.mizuho-ir.co.jp/publication/report/2020/fe36.html )。
ファクター分析で扱われているファクターは、リターンの要因として定義され、株価にも何らかの影響力があると考えられたものです。様々なファクターについて勉強することが、特徴量設計の次の一歩に繋がるでしょう。
7.9. 複数個のモデルの出力をアンサンブルするアプローチ
アンサンブルの活用について説明します。機械学習における「アンサンブル」とは、複数のモデルを組み合わせることでパフォーマンスの高いモデルを作成する手法を意味します。アンサンブルに使うモデルは多様性があればある程基本的には好ましく、多様性のあるモデルを作り、最終的にアンサンブルすることで、単一モデルでは達成できないパフォーマンスを最終的に達成する可能性があります。
アンサンブルには、シンプルに複数のモデルの出力の平均を取るモデル平均法、scikit-learnライブラリのStandardScaler( https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html )による標準化を実施して分布をある程度揃えてから足し合わせる方法などがあります。また、より高度な手法であるスタッキングもscikit-learnライブラリにはStackingClassifer/StackingRegressorがあるため容易に実施(スタッキングで分類・回帰 (scikit-learn) より引用 https://qiita.com/maskot1977/items/de7383898123fa378d86 )することが可能です。kaggleで活用されている様々なアンサンブルの方法がKAGGLE ENSEMBLING GUIDE( https://mlwave.com/kaggle-ensembling-guide/ )では紹介されており、英文ですが読む価値があります。
ここでは、時価総額に着目して学習の対象を分けて複数個のモデルを作るアプローチを考えてみます。一般的に時価総額が低い銘柄は、大きな値動きが発生しやすいことが知られています。これは市場の流動性に違いがあり、同一額の投資が発生しても、小型株のほうがよりインパクトが大きいためです。今回のコンペティションでは、全銘柄を予測対象としていますが、実際にモデルを作ると全銘柄の時価総額の下位の銘柄を学習対象から除外すると、よりモデルのパフォーマンスが高くなることがあります。これは時価総額が低い銘柄は、ランダム性がより高く、またファンダメンタルに従わないことが多いためです。
では、以下の2つのモデルをつくった場合を考えてみます。
A: 全銘柄を対象に学習したモデル
B: 時価総額の下位の銘柄を学習から除外した上で、パフォーマンスをチューニングしたモデル
この2つが異なることを学習したとした場合、Bのモデルの出力に対してStandardScalerによる標準化を実施し、Aのモデルの出力に足し合わせると、Bのモデルが学んだことをBの学習対象の銘柄に足し合わせることができます。Bの出力に対しては、StandardScalerによる標準化を実施しているため分布が0平均となっており、学習対象外の銘柄に対する影響も限定することができます。
異なる特性をもったデータを学習させることで、モデルが異なることを学び、結果的にモデル同士の出力の相関が低くなります。モデル間の出力の相関が低いもの同士をアンサンブルさせると、相関の高いもの同士をアンサンブルさせた時よりも、アンサンブルの効果は高く出ることが多いため、上記のように学習対象を変えることで複数のモデルを作り、アンサンブルを実施するようなアプローチは有用です。
7.10. プライベート期間の性能の向上のために考慮すべきこと
金融時系列はサンプル数が少ないため、特徴量を大量に生成し、特徴量選択をすべてモデルに任せるアプローチを採用する場合、ライブ性能の劣化に注意する必要があります。特徴量をどんどん増やすと、訓練期間のパフォーマンスは伸びていても、評価期間のパフォーマンスの向上が止まることがあります。100種類のデータを使うモデルと10種類のデータを使うモデルが、同一の訓練期間で同一の精度を達成した場合、評価期間・ライブ期間では、少ないデータを使ったモデルの方が高い性能を期待できる可能性が高いことが、経験的にわかっています。これは、説明変数の取りうるパターンが多いと、未来で同じ現象を発生する確率が下がっていくためと考えられます。モデルの複雑さとデータへの適合度とのバランスを取るためには、オッカムの剃刀(Wikipedia オッカムの剃刀より引用 https://ja.wikipedia.org/wiki/%E3%82%AA%E3%83%83%E3%82%AB%E3%83%A0%E3%81%AE%E5%89%83%E5%88%80 ) のような発想が必要となります。
7.11. 本コンペでは利用できないが、モデルを将来的に発展させるために検討する価値のある外部データ
日本株のデータ以外に特徴量設計に利用可能と思われるデータを紹介します。本コンペでは、あらかじめ定められたデータしか利用することはできませんが、今後手元で新たなモデルを作成するときの知識としてご活用下さい。
為替データ: ドル円の値動きが株式市場に影響を与えていることはよく知られています。特に日本市場の株式は輸出関連銘柄が多いため、ドル円の値動きは直接収益に関連します。よって、為替データを説明変数に採用するアプローチも想定されます。為替データは、いくつかのFX会社がAPIを提供しています。
金利データ: 金利データとは、例えば米国債10年金利のような各国の債券の金利を指します。一般的に、機関投資家は債券と株式の両方を投資対象とするため、債券市場の動きは株式市場に反映されます。こちらは、APIによるデータ習得は容易ではありませんが、そこまで数は多くないため、説明変数として利用することは難しくありません。
米国株データ: Alpaca US( https://alpaca.markets/data )やIEX Cloud( https://iexcloud.io/ )など、様々な米国株の株価/ETFのデータを提供するサービスが存在します。日本株式のマーケットは、米国株式のマーケットクローズ後にオープンするため、米国市場が日本市場に与える影響を解析することで、様々な情報を分析することが可能です。
他にも政府が発表するGDPなどの各国の経済動向、金などのコモディティ市場も、密接に株式市場の長期トレンドの形成に関わっていますので、様々な外部データの利用を検討することで新たなモデルを作ることができる可能性があります。
7.12. モデルの再学習の運用について
長期間に渡りモデルを運用しようとする場合、再学習の運用を考慮しておく必要があります。再学習の運用とは、例えば2019年までのデータを用いてモデルを学習し2020年で運用した場合、2020年末に2020年のデータを用いて再学習を行うといったようなことを指します。再学習を行うにあたっていくつか考慮しておくべきポイントを紹介します。
7.12.1. 再学習を行う必要があるほど新規のデータが存在するか
再学習は、新規のデータが溜まった時に実施します。モデルにも依存しますが、モデルが挙動を変えるには、既存の学習に用いたデータ量と比較してある程度の量の新規データが存在しないと、再学習を実施してもモデルの挙動は変わりません。再学習する際に有用な新規データ量は一概には言えず、モデルによって変わります。毎日モデルをトレーニングするような運用も可能ですが、データ量が多少増えただけでは、ほぼ同じ挙動となる可能性が高いです。
7.12.2. 再学習を行うことでモデルの出力分布が変わらないか
こちらは、システムで運用する場合に発生しやすい問題です。例えば、投資する際の購入タイミングを、モデルの出力が0.8以上といったしきい値を用いた実装をしていたとします。この際に再学習を行うことでモデルの出力が変わると、想像以上に購入したり、逆に購入を実施しなくなったりします。再学習を行った場合、直近数週間程度のデータは利用せずに、古いモデルと新しいモデルで出力を比較し、出力の分布が変わっていないことを確認するのが良いでしょう。
7.13. Google Colaboratoryの使用法
Google Colaboratoryは、ブラウザから Python をノートブック形式で記述、実行できるサービスです。環境構築が不要となっており、本チュートリアルもGoogle Colaboratoryで実行することが可能となっています。また、時間等の制限はございますがGPUを利用できることや、ノートブックの共有が簡単にできることなど、多くの利点を備えています (参考元 )。
7.13.1. Colab でノートブックが動作する時間は?
本チュートリアルをGoogle Colaboratoryで実行する際には時間制限にご注意ください。ノートブックは、インスタンスが起動された後 12 時間経過すると自動的にランタイムがリセットされ実行環境が初期化されます。また、ノートブックのアイドル状態が 90 分続くとタイムアウトし、こちらもランタイムがリセットされます。(詳細はGoogle ColaboratoryのQ&Aをご参照ください。)。
7.13.2. 2章でGoogle Colaboratoryを使用するために
本コンペの2章のチュートリアルをGoogle Colaboratory上で動かすためには、まず以下の手順でGoogle Drive上にファイルを設置します。
-
Google DriveのMy Driveに
JPX_competitionというフォルダーを作成します。 -
SIGNATEのコンペティションサイトよりダウンロードした各種データを1で作成したフォルダーにアップロードします。
次にGoogle Colaboratory上でチュートリアルのノートブックを展開します。ノートブックはGoogle Colaboratory上でも実行可能となっており、そのまま編集なしで実行できます。以下、具体的な方法を説明します。
-
ノートブックをダウンロードします。 こちらのGithubリポジトリよりRawボタンを右クリックし、「リンク先を名前をつけて保存」を選択して先程作成した
JPX_competitionに保存してください。 -
Google Driveにアップロードした
20210121-chapter02-tutorial.ipynbファイルをダブルクリックして Google Colaboratory で開きます。 -
コンペティションデータをノートブックで読み込むために、Google Driveへマウントします。マウント方法についてはこちらの記事をご参照ください。
7.14. 内国株の売買制度
本節では、本コンペティションの題材となっている株式の売買制度について説明します。
7.14.1. 制限値幅
東京証券取引所では、一日の売買における値動きの幅を価格水準に応じて一定に制限しており、この値幅を 制限値幅 といいます。制限値幅は、前日の終値又は最終気配値段など(以下、「基準値段」と言います)を基準としており、その値幅の大きさは基準値段によって異なります。詳細はこちらをご参照ください。
7.14.2. 呼値の単位
内国株式の売買の注文をする際の値段の刻みことを 呼値の単位 といい、この呼値の単位は、売買の対象となる銘柄及びその値段の水準に応じて異なります。各値段の水準における詳細な呼値の単位については、こちらをご参照ください。なお、銘柄によっては呼値の単位は整数ではなく、小数点があるものもございますのでご留意ください。
7.15. バックテスト用ライブラリ
有名なバックテスト/ポートフォリオライブラリとしてはZipline( https://github.com/quantopian/zipline )やBacktrader( https://github.com/mementum/backtrader )があります。Ziplineは人気のあるライブラリでしたが、開発元のQuantopianがなくなったため、現在開発が止まっています。Backtraderは機能が多用ですが、初心者には若干敷居が高いです。バックテストライブラリは定番と言えるものが無く、取引戦略を実装する場合、フレームワークは利用せず個別に自分の取引戦略に合致したバックテストのコードを書いて評価し、結果はmatplotlibなどの描画用ライブラリで直接描画することも多く、本チュートリアルもその方式を採用しています。
ポートフォリオを構築せずに、まずはポートフォリオを構築するための予測モデル自体の評価を情報係数(IC)や分位点リターンなどを利用して行うバックテストも存在します。その手法は本チュートリアルでは扱いませんが、qlib( https://github.com/microsoft/qlib )やalphalense( https://github.com/quantopian/alphalens )などのライブラリに様々な方法が紹介されていますので、是非御覧ください。日本語ではあまり網羅的なサイトは無いのですが、書籍で紹介した「ファイナンス機械学習―金融市場分析を変える機械学習アルゴリズムの理論と実践」において網羅的な説明がされています。
| ライブラリ名 | 説明 | Github |
|---|---|---|
Zipline |
イベント駆動型のアルゴリズムトレーディングのバックテストライブラリ |
|
backtrader |
バックテストとライブトレードのライブラリ |
|
qlib |
Microsoftの開発するAI投資向けのバックテストライブラリ |
|
alphalense |
株式ファクターにフォーカスしたバックテストライブラリ |
8. J-QuantsAPI
8.1. 概要
この章では、各種データをダウンロードできるJ-QuantsAPIについてご紹介します。APIの詳細な仕様はこちら("https://jpx-jquants.com/apidoc.html")をご確認ください。
8.2. APIの利用
APIを利用するには、SIGNATEでのコンペティションへのご登録とJ-QuantsAPIの利用登録が必要となります。
8.3. 必要なパッケージのインポート
import os
import json
import requests
import base64| パッケージ名 | 目的 |
|---|---|
os |
ディレクトリ、ファイル操作のため |
json |
レスポンスの加工のため |
requests |
APIのGETやPOSTを利用するため |
base64 |
TDnetのファイルダウンロードAPIでBase64形式で返ってくるデータをデコードするため |
8.4. Refresh API
はじめに、idTokenをリフレッシュするRefresh API("/refresh")をご紹介します。このAPIでは、J-Quantsのログイン後の画面でご確認いただくことができるrefreshTokenを使用します。
Refresh APIを使うためのサンプルコードは以下のようになります。
def call_refresh_api(refreshtoken: str):
"""
idTokenをリフレッシュするメソッド。
Parameters
----------
refreshtoken : str
refreshtoken。ログイン後の画面からご確認いただけます。
Returns
-------
resjson : dict
新しいidtokenが格納されたAPIレスポンス(json形式)
"""
headers = {"accept": "application/json"}
data = {"refresh-token": refreshtoken}
response = requests.post(
"https://api.jpx-jquants.com/refresh", headers=headers, data=json.dumps(data)
)
resjson = json.loads(response.text)
return resjsonこのAPIを使うことで新しいidtokenを払い出すことができます。使用例は以下の通りです。
refreshtoken = <Your refreshtoken>
call_refresh_api(refreshtoken)以下のようなレスポンスが返ります。なお、idtokenの有効期限は1時間(3600sec)となっております。
{"idToken": "<Your New idtoken>",
"expiresIn": 3600}8.5. 共通で使用するメソッド
ここでは、API共通の関数を用意しております。
サンプルコードは以下の通りです。引数"apitype"に各APIを指定することで呼び出すことができます。
def call_jquants_api(params: dict, idtoken: str, apitype: str, code: str = None):
"""
J-QuantsのAPIを試すメソッド。
Parameters
----------
params : dict
リクエストパラメータ。
idtoken : str
idTokenはログイン後の画面からご確認いただけます。
apitype: str
APIの種類。"news", "prices", "lists"などがあります。
code: str
銘柄を指定するAPIの場合に設定します。
Returns
-------
resjson : dict
APIレスポンス(json形式)
"""
datefrom = params.get("datefrom", None)
dateto = params.get("dateto", None)
date = params.get("date", None)
includedetails = params.get("includedetails", "false")
keyword = params.get("keyword", None)
headline = params.get("headline", None)
paramcode = params.get("code", None)
nexttoken = params.get("nextToken", None)
headers = {"accept": "application/json", "Authorization": idtoken}
data = {
"from": datefrom,
"to": dateto,
"includeDetails": includedetails,
"nextToken": nexttoken,
"date": date,
"keyword": keyword,
"headline": headline,
"code": paramcode,
}
if code:
code = "/" + code
r = requests.get(
"https://api.jpx-jquants.com/" + apitype + code,
params=data,
headers=headers,
)
else:
r = requests.get(
"https://api.jpx-jquants.com/" + apitype, params=data, headers=headers
)
resjson = json.loads(r.text)
return resjson8.6. Stock Lists API
銘柄一覧を取得するAPIについて紹介いたします。
このAPIでは、企業名や業種区分などの基本情報を取得することができます。全銘柄の一覧を取得する"/lists"と銘柄コードを指定した"/lists/{code}"が利用できます。
idtk=<your idtoken>
# Codeを指定しない場合
paramdict = {}
paramdict["includedetails"] = "True"
call_jquants_api(paramdict, idtk, "lists")
# Codeを指定する場合
paramdict = {}
paramdict["includedetails"] = "True"
call_jquants_api(paramdict, idtk, "lists", "8697")レスポンスは以下のようになります。
{"list": [{"33 Sector(name)": "Other Financing Business",
"Effective Date": "20201230",
"prediction_target": "True",
"Section/Products": "First Section (Domestic)",
"33 Sector(Code)": 7200.0,
"Name (English)": "Japan Exchange Group,Inc.",
"IssuedShareEquityQuote IssuedShare": 536351448.0,
"Local Code": "8697"}]}8.7. Prices API
株価情報を取得するPrice APIをご紹介します。
検索期間や銘柄コードを指定することで、四本値、売買高、前日比変化率などを取得することができます。銘柄コードを指定する場合は"/prices/{code}"でAPIをご利用ください。"includeDetails"をTrueにした場合は、全てのデータ系列を取得します。
idtk=<your idtoken>
# Codeを指定しない場合
paramdict = {}
paramdict["date"] = "2020-12-30"
paramdict["includedetails"] = "True"
call_jquants_api(paramdict, idtk, "prices")
# Codeを指定する場合
paramdict = {}
paramdict["datefrom"] = "2020-01-17"
paramdict["dateto"] = "2020-01-31"
paramdict["includedetails"] = "True"
call_jquants_api(paramdict, idtk, "prices", "8697")レスポンスのサンプルは以下の通りです。
{"prices": [{"EndOfDayQuote Open": 2005.0,
"EndOfDayQuote PreviousClose": 1972.0,
"EndOfDayQuote CumulativeAdjustmentFactor": 1.0,
"EndOfDayQuote VWAP": 1994.792,
"EndOfDayQuote Low": 1989.0,
"EndOfDayQuote PreviousExchangeOfficialClose": 1972.0,
"EndOfDayQuote High": 2008.0,
"EndOfDayQuote Date": "2020/01/20",
"EndOfDayQuote Close": 1990.0,
"EndOfDayQuote PreviousExchangeOfficialCloseDate": "2020/01/17",
"EndOfDayQuote ExchangeOfficialClose": 1990.0,
"EndOfDayQuote ChangeFromPreviousClose": 18.0,
"EndOfDayQuote PercentChangeFromPreviousClose": 0.913,
"EndOfDayQuote PreviousCloseDate": "2020/01/17",
"Local Code": "8697",
"EndOfDayQuote Volume": 528600.0},
{"EndOfDayQuote Open": 1989.0,
"EndOfDayQuote PreviousClose": 1990.0,
"EndOfDayQuote CumulativeAdjustmentFactor": 1.0,
"EndOfDayQuote VWAP": 1976.539,
"EndOfDayQuote Low": 1965.0,
"EndOfDayQuote PreviousExchangeOfficialClose": 1990.0,
"EndOfDayQuote High": 1995.0,
"EndOfDayQuote Date": "2020/01/21",
"EndOfDayQuote Close": 1977.0,
"EndOfDayQuote PreviousExchangeOfficialCloseDate": "2020/01/20",
"EndOfDayQuote ExchangeOfficialClose": 1977.0,
"EndOfDayQuote ChangeFromPreviousClose": -13.0,
"EndOfDayQuote PercentChangeFromPreviousClose": -0.653,
"EndOfDayQuote PreviousCloseDate": "2020/01/20",
"Local Code": "8697",
"EndOfDayQuote Volume": 571000.0},
...]}8.8. Stock Fins API
各銘柄の財務諸表データを取得するAPIをご紹介します。
特定の日の全銘柄の情報を取得する"/stockfins"と1銘柄の情報を取得する"/stockfins/{code}"がございます。
idtk=<your idtoken>
# Codeを指定しない場合
paramdict = {}
paramdict["date"] = "2020-12-30"
paramdict["includedetails"] = "True"
call_jquants_api(paramdict, idtk, "stockfins")
# Codeを指定する場合
paramdict = {}
paramdict["datefrom"] = "2020-01-01"
paramdict["dateto"] = "2020-12-30"
paramdict["includedetails"] = "True"
call_jquants_api(paramdict, idtk, "stockfins", "8697")レスポンスは以下のようになります。
{"stockfin": [{"Result_FinancialStatement TotalAssets": 56671198.0,
"base_date": "2020/01/30",
"Result_FinancialStatement FiscalPeriodEnd": "2019/12",
"Result_FinancialStatement ReportType": "Q3",
"Result_FinancialStatement OrdinaryIncome": 48586.0,
"Result_FinancialStatement CashFlowsFromOperatingActivities": "",
"Local Code": "8697",
"Result_FinancialStatement NetSales": 87433.0,
"Result_FinancialStatement CashFlowsFromFinancingActivities": "",
"Result_FinancialStatement CashFlowsFromInvestingActivities": "",
"Result_FinancialStatement AccountingStandard": "ConsolidatedIFRS",
"Result_FinancialStatement NetIncome": 33317.0,
"Result_FinancialStatement OperatingIncome": 48176.0},
{"Result_FinancialStatement TotalAssets": 56671198.0,
"base_date": "2020/03/23",
"Result_FinancialStatement FiscalPeriodEnd": "2019/12",
"Result_FinancialStatement ReportType": "Q3",
"Result_FinancialStatement OrdinaryIncome": 48586.0,
"Result_FinancialStatement CashFlowsFromOperatingActivities": "",
"Local Code": "8697",
"Result_FinancialStatement NetSales": 87433.0,
"Result_FinancialStatement CashFlowsFromFinancingActivities": "",
"Result_FinancialStatement CashFlowsFromInvestingActivities": "",
"Result_FinancialStatement AccountingStandard": "ConsolidatedIFRS",
"Result_FinancialStatement NetIncome": 33317.0,
"Result_FinancialStatement OperatingIncome": 48176.0}]}8.9. Stock Labels API
基準日から一定期間の株価の最大上昇率、最大下落率を取得するAPIをご紹介します。
Stock Labels APIは期間や銘柄コードを指定することで該当する株価騰落率のデータを取得できます。
# Codeを指定しない場合
paramdict = {}
paramdict["date"] = "2018-05-31"
paramdict["includedetails"] = "true"
call_jquants_api(paramdict, idtk, "stocklabels")
# Codeを指定する場合
paramdict = {}
paramdict["from"] = "2020-02-01"
paramdict["to"] = "2020-02-28"
paramdict["includedetails"] = "true"
call_jquants_api(paramdict, idtk, "stocklabels", "1301")レスポンスのサンプルは以下の通りです。
{"labels": [{"label_low_10": -0.01748,
"label_low_20": -0.10699,
"label_low_5": 0.0021,
"label_high_20": 0.02203,
"base_date": "2020-02-04",
"label_high_10": 0.02203,
"label_date_5": "2020-02-12",
"label_date_10": "2020-02-19",
"label_high_5": 0.02203,
"label_date_20": "2020-03-05",
"Local Code": "1301"},
{"label_low_10": -0.02507,
"label_low_20": -0.11072,
"label_low_5": -0.00557,
"label_high_20": 0.01776,
"base_date": "2020-02-05",
"label_high_10": 0.01776,
"label_date_5": "2020-02-13",
"label_date_10": "2020-02-20",
"label_high_5": 0.01776,
"label_date_20": "2020-03-06",
"Local Code": "1301"}],
"scrollId": "eyJMb2NhbCBDb2RlIjogIjEzMDEiLCAiYmFzZV9kYXRlIjogIjIwMjAtMDItMDUifQ=="}8.10. News API
日経新聞の記事情報を取得するAPIをご紹介します。
News APIはヘッドライン、キーワード、期間などで該当するニュース記事データを検索できます。
idtk=<your idtoken>
paramdict = {}
paramdict["datefrom"] = "2020-02-01"
paramdict["dateto"] = "2020-02-25"
paramdict["code"] = "8697"
paramdict["headline"] = "日本取引所"
paramdict["keyword"] = "エネルギー"
call_jquants_api(paramdict, idtk, "news")レスポンスフィールドの詳細は以下の通りです。
-
media_code: 媒体の略号です。今回は"TNY"のデータのみ提供しております。
-
men_name: 面の名前です。地方経済面の場合などに収録されますが、今回は全て""です。
-
headline: 見出しです。改行コード"\n"が含まれます。
-
keywords: 記事の文中から主題語として切り出したキーワードです。改行コード"\n"でそれぞれのキーワードが区切られております。
-
classifications: 記事の分類です。当該記事に紐づくさまざまなコードが収録されております。マスタデータは こちらからダウンロードいただけます。
-
"#W〜": 記事の主題を表す内容別の136分類です。分類体系は「企業活動」(大分類:企業)と「企業を取り巻く環境」(大分類:政治・経済・技術・社会)から構成しております。マスタデータはtheme.csvをご参照ください。
-
"#B〜": 記事の主題と関連する業界別の63分類です。日経新業種分類を元に定義しております。マスタデータはindustry.csvをご参照ください。
-
"#A〜": 記事の主題と関連する地域別に「海外地域」「国」「国内地域」単位で分類しております。マスタデータはregion.csvをご参照ください。
-
"#K〜": 記事種別です。記事のタイプ別に7種類に分類しております。
-
"#T〜": 株式コードです。
-
"#N〜": 日経会社コードです。
-
"#PD〜": 業界コードです。株式コードおよび一部主要企業の日経会社コードを一括して指定可能なコードです。マスタデータはindustry2.csvをご参照ください。
-
コラム名: 主要なコラムや大型連載記事が検索可能です。例えば「春秋」など。
-
"$〜": 記事分類キーワードです。新聞を紙面単位で指定可能です。
-
レスポンスのサンプルは以下の通りです。
{"news": [{"article_id": "TDSKDBDGXLASFL21HM9_21022020000000",
"publish_datetime": "2020-02-21T16:34:00Z",
"media_code": "TNY",
"media_name": "日本経済新聞電子版",
"men_name": "",
"headline": "日本取引所CEO、東商取のエネルギー市場「早期に統合したい」",
"keywords": "最高経営責任者\n東京商品取引所\n日本取引所グループ\n清田瞭\nエネルギー市場\n大阪取引所\n統合\n定例\n早期",
"classifications": "T8697\nPD521\nN0040431\nN0075107\nN0040779",
"stock_code": "8697"}],
"scrollId": "FGluY2x1ZGVfY29u"}8.11. TDnet API
適時開示を取得できるTDnetAPIを紹介します。
TDnetAPIはTDnetで開示された資料に関する情報を取得、またはダウンロードすることができるapiです。
資料に関する情報を取得するAPIは、通常は("/tdfiles")、銘柄コードを指定する場合は、”/tdnet/{code}でAPIをご利用ください。 "includeDetails"をTrueにした場合は、全てのデータ系列を取得します。
idtk=<your idtoken>
# Codeを指定しない場合
paramdict = {}
paramdict["date"] = "2020-12-30"
paramdict["includedetails"] = "True"
call_jquants_api(paramdict, idtk, "tdnet")
# Codeを指定する場合
paramdict = {}
paramdict["datefrom"] = "2020-01-01"
paramdict["dateto"] = "2020-02-28"
paramdict["includedetails"] = "True"
call_jquants_api(paramdict, idtk, "tdnet", "8697")レスポンスのサンプルは以下のようになります。なおdisclosureItemsは公開項目コードを示します。一覧はこちらからダウンロードください。
{"tdnet": [{"pdfSumaryFlag": "1",
"modifiedHistory": "1",
"name": "JPX",
"disclosureItems": ["11384"],
"code": "86970",
"disclosedDate": "2020-01-30",
"datetime": "2020-01-30:12:00:00",
"handlingType": None,
"disclosedTime": "12:00:00",
"pdfGeneralFlag": "1",
"disclosureNumber": "20200129453073",
"xbrlFlag": "1",
"title": "2020年3月期 第3四半期決算短信〔IFRS〕(連結) "},
{"pdfSumaryFlag": "0",
"modifiedHistory": "1",
"name": "JPX",
"disclosureItems": ["11804"],
"code": "86970",
"disclosedDate": "2020-01-30",
"datetime": "2020-01-30:12:00:00",
"handlingType": None,
"disclosedTime": "12:00:00",
"pdfGeneralFlag": "1",
"disclosureNumber": "20200129453074",
"xbrlFlag": "0",
"title": "Consolidated financial results for the nine months ended December 31, 2019"},
...]}公開項目コードを用いると出力結果を絞ることが可能です。 例えば、第三四半期決算短信(連結・日本基準・公開項目コード11310)は以下のようなコードとなります。
resp = call_jquants_api({}, idtk, "tdnet")
[f for f in resp["tdnet"] if "11310" in f["disclosureItems"]]こちらのコードを実行すると、第3四半期決算短信のみ抽出することができます。
[{"name": "J-インターライフ",
"disclosureItems": ["11310"],
"datetime": "2021-01-13:16:00:00",
"code": "14180",
"handlingType": None,
"disclosureNumber": "20210112443207",
"title": "2021年2月期\u3000第3四半期決算短信〔日本基準〕(連結)"},
{"name": "S\u3000FOODS",
"disclosureItems": ["11310"],
"datetime": "2021-01-13:15:00:00",
"code": "22920",
"handlingType": None,
"disclosureNumber": "20210113443358",
"title": "2021年2月期第3四半期決算短信〔日本基準〕(連結)"},
{"name": "いちご",
"disclosureItems": ["11310"],
"datetime": "2021-01-13:15:00:00",
"code": "23370",
"handlingType": None,
"disclosureNumber": "20210113443616",
"title": "2021年2月期 第3四半期 決算短信〔日本基準〕(連結)"},
...]このAPIのレスポンスのdisclosureNumberを用いることで、PDFファイルやXBRLファイルを取得する(/tdfiles)もございます。
決算短信はサマリ-PDF("fileTypeFlag"が"s")やXBRL("fileTypeFlag"が"x")をダウンロードすることができます。そのほかの資料は全文PDFのみですので、("fileTypeFlag"が"g")をご指定ください。
ただし、これらのファイルが取得できるものは2020年以降開示されたものに限ります。
def call_tdfiles_api(params: dict, idtoken: str, outputdir: str = None):
"""
TDnetで開示された資料をダウンロードするAPI。
Parameters
----------
params : dict
リクエストパラメータ。
idtoken : str
idtokenはログイン後の画面からご確認いただけます。
outputdir : str
ダウンロードしたファイルを格納するフォルダパスを指定いただけます。
"""
disclnum = params.get("disclosurenumber")
ftype = params.get("filetypeflag", "g")
if not outputdir:
outputdir = ""
headers = {"Authorization": idToken, "accept": "application/json"}
data = {"disclosureNumber": disclnum, "fileTypeFlag": ftype}
r = requests.get(
"https://api.jpx-jquants.com/tdfiles", params=data, headers=headers
)
resjson = json.loads(r.text)
if resjson["responseType"] == "1":
bjson = resjson["fileData"].encode()
elif resjson["responseType"] == "2":
filedata = requests.get(resjson["fileUrl"]).text
bjson = filedata.encode()
if ftype == "x":
fname = outputdir + "/x_" + disclnum + ".zip"
elif ftype == "g":
fname = outputdir + "/g_" + disclnum + ".pdf"
elif ftype == "s":
fname = outputdir + "/s_" + disclnum + ".pdf"
with open(fname, "wb") as theFile:
theFile.write(base64.b64decode(bjson))
print("Finish Download: " + disclnum)このメソッドを利用することで、base64形式のデータをファイルに書き出すことが可能です。実際にこのメソッドを利用する方法は以下の通りです。
idtk=<your idtoken>
# 出力フォルダを指定
outputdir = "./"
# 全文PDFを取得する場合
paramdict = {}
paramdict["disclosurenumber"] = "20200129453073"
paramdict["filetypeflag"] = "g"
call_tdfiles_api(paramdict, idtk, outputdir)
# サマリーPDFを取得する場合(決算短信で指定可能です)
paramdict = {}
paramdict["disclosurenumber"] = "20200129453073"
paramdict["filetypeflag"] = "s"
call_tdfiles_api(paramdict, idtk, outputdir)
# XBRLデータを取得する場合(決算短信で指定可能です)
paramdict = {}
paramdict["disclosurenumber"] = "20200129453073"
paramdict["filetypeflag"] = "x"
call_tdfiles_api(paramdict, idtk, outputdir)9. チュートリアル作成環境の参考文献
本文書の執筆では次のプロダクトと技術資料が使われています。
| プロダクト名の隣にライセンスを併記しております。 |
- Template
-
-
AsciidoctorとGradleでつくる文書執筆環境 - MIT License - https://h1romas4.github.io/asciidoctor-gradle-template/index.html
-
- Font
-
-
源真ゴシック - SIL Open Font License 1.1 - http://jikasei.me/font/genshin/
-
源様明朝 - SIL Open Font License 1.1 - https://github.com/ButTaiwan/genyo-font
-
Ricty Diminished - SIL Open Font License 1.1 - https://github.com/edihbrandon/RictyDiminished
-
- Asciidoc
-
-
Asciidoctor - MIT License - https://asciidoctor.org/
-
Asciidoctorj - Apache License 2.0 - https://github.com/asciidoctor/asciidoctorj
-
Asciidoctor.js - MIT License - https://asciidoctor.org/docs/asciidoctor.js/
-
Asciidoctor PDF - MIT License - https://asciidoctor.org/docs/asciidoctor-pdf/
-
Asciidoctor Gradle Plugin Suite - Apache License 2.0 - https://github.com/asciidoctor/asciidoctor-gradle-plugin
-
asciidoctor-pdf-linewrap-ja - MIT License - https://github.com/fuka/asciidoctor-pdf-linewrap-ja
-
- Build Tool
-
-
SDKMAN - Apache License 2.0 - https://sdkman.io/
-
Gradle - Apache License 2.0 - https://gradle.org/
-
- Text Editor
-
-
Visual Studio Code - Microsoft - https://code.visualstudio.com/
-
asciidoctor-vscode - MIT License - https://github.com/asciidoctor/asciidoctor-vscode
-
- Guide
-
-
asciidoctor-pdfでかっこいいPDFを作る - https://qiita.com/kuboaki/items/67774c5ebd41467b83e2
-
- OGP
-
-
Socialify - https://github.com/wei/socialify
-
9.1. 商標
-
Windows、PowerShellは、Microsoft Corporation の登録商標または商標です。
-
Docker は、Docker Inc.の登録商標または商標です。
-
CoLaboratory™ は、Google Inc. の登録商標または商標です。
-
GitHub は、GitHub Inc.の登録商標または商標です
10. ライセンス
本チュートリアルおよびハンズオンのソースコードは CC BY-NC-ND 4.0 に従うライセンスで公開しています。
教育など非商用の目的での本チュートリアルの使用や再配布は自由に行うことが可能です。 商用目的で本チュートリアルの全体またはその一部を無断で転載する行為は,これを固く禁じます。
